Lösningar 21

Matematik för naturvetare 15hp

(Skillnad mellan versioner)
Hoppa till: navigering, sök
Versionen från 2 oktober 2007 kl. 13.35 (redigera)
Clas Löfwall (Diskussion | bidrag)
(Ny sida: ==Lösningar till några övningar till lektion 21== Tillbaka till lösningarna)
← Gå till föregående ändring		 Versionen från 26 oktober 2007 kl. 10.55 (redigera) (ogör)
Clas Löfwall (Diskussion | bidrag)

Gå till nästa ändring →
Rad 1: Rad 1:
==Lösningar till några övningar till lektion 21== ==Lösningar till några övningar till lektion 21==
 +
 +
 +'''13.12.'''
 +
 +Skriv ekvationen som \begin{array}
 +y'-\frac{2}{x}\, y=x+\frac{1}{x}.\end{array}
 +En primitiv funktion till $-2/x$ är $-2\ln x$ (observera att $x>0$), så en integrerande faktor är $e^{-2\ln x}=x^{-2}=1/x^2$. Multiplicerar vi (1) med den så får vi <math>
 +\frac{1}{x^2}\, y'-\frac{2}{x^3}\, y=\frac{1}{x}+\frac{1}{x^3}</math>
 +som kan skrivas <math>
 +\frac{d}{dx}\,\left(\frac{1}{x^2}\, y\right)=\frac{1}{x}+\frac{1}{x^3}.</math>
 +Alltså är <math>
 +\frac{1}{x^2}\, y=\ln x-\frac{1}{2x^2}+C,</math> där $C$ är en konstant,
 +eller <math>
 +y=x^2\ln x-\frac{1}{2}+Cx^2.</math>
 +Villkoret $y(1)=0$ ger $-1/2+C=0$, dvs $C=1/2$, så den sökta lösningen är <math>
 +y=x^2\ln x-\frac{1}{2}+\frac{1}{2}\,x^2.</math>
 +
 +
 +
 +'''13.13.'''
 +
 +Ekvationen kan skrivas <math>
 +y'-\frac{2}{x}\, y=\frac{x^2}{2}.</math>
 +En primitiv funktion till $-2/x$ är $-2\ln x$ (ty $x>0$), så en integrerande faktor är $e^{-2\ln x}=1/x^2$. Multiplicerar vi med den så får vi <math>
 +\frac{1}{x^2}\, y'-\frac{2}{x^3}\, y=\frac{1}{2}</math>
 +som kan skrivas <math>
 +\frac{d}{dx}\left(\frac{1}{x^2}\, y\right)=\frac{1}{2}.</math>
 +Alltså är <math>
 +\frac{1}{x^2}\, y=\frac{x}{2}+C,</math> där $C$ är en konstant,
 +eller <math>
 +y=\frac{x^3}{2}+Cx^2.</math>
 +Villkoret $y(1)=0$ ger $1/2+C=0$, så $C=-1/2$ och den sökta lösningen är <math>
 +y=\frac{x^3}{2}-\frac{x^2}{2}=\frac{1}{2}\,(x^3-x^2).</math>
 +
 +
 +
 +'''13.15.'''
 +
 +Vi skriver ekvationen som <math>
 +y'+\frac{2}{x-1}\, y=-\frac{x^3}{x-1}.</math>
 +En primitiv funktion till $2/(x-1)$ är $2\ln(x-1)$ (observera att $x>1$), så en integrerande faktor är $e^{2\ln(x-1)}=(x-1)^2$. Multiplicerar vi med den så får vi <math>
 +(x-1)^2y'+2(x-1)y=-x^3(x-1),</math>
 +som kan skrivas <math>
 +\frac{d}{dx}\left((x-1)^2y\right)=-x^3(x-1)=x^3-x^4.</math>
 +Alltså är <math>
 +(x-1)^2y=\frac{x^4}{4}-\frac{x^5}{5}+C,</math> där $C$ är en konstant,
 +varav <math>
 +y=\frac{x^4/4-x^5/5+C}{(x-1)^2}.</math>
 +
 +
 +
 +'''13.17.'''
 +
 +Vi skriver ekvationen som <math>
 +y'-\frac{2\cos x}{\sin x}\, y=\frac{\cos x}{\sin x}</math>
 +och måste hitta en primitiv funktion till $-2\cos x/\sin x$. En substitution löser problemet:<math>
 +\int\frac{\cos x}{\sin x}\, dx=\left\{\begin{array}{ccccc}
 +\sin x&=&t\\
 +\cos x\, dx&=&dt\end{array}\right\}=
 +\int\frac{dt}{t}=\ln |t|+C=\ln|\sin x|+C.</math>
 +Vi väljer den primitiva funktionen $-2\ln|\sin x|$ och får den integrerande faktorn <math>
 +e^{-2\ln|\sin x|}=(|\sin x|)^{-2}=\frac{1}{\sin^2x}.</math>
 +Multiplicerar vi med den så får vi <math>
 +\frac{1}{\sin^2x}\, y'-\frac{2\cos x}{\sin^3x}\, y=\frac{\cos x}{\sin^3x}</math>
 +som kan skrivas <math>
 +\frac{d}{dx}\left(\frac{1}{\sin^2x}\, y\right)=\frac{\cos x}{\sin^3x}.</math>
 +Med samma substitution som nyss så får vi att $-1/2\sin^2x+C$ är de primitiva funktionerna till HL, varför <math>\frac{1}{\sin^2x}\, y=-\frac{1}{2\sin^2x}+C\quad\mbox{eller}\quad
 +y=-\frac{1}{2}+C\sin^2x.</math>
 +
 +
 +
 +'''13.19.'''
 +
 +Beteckna klorhalten vid tiden $t$ dygn med $y(t)$ (mätt som liter klor per liter klorhaltigt vatten i cisternen). Mellan tidpunkterna $t$ och $t+\Delta t$ läcker $300\Delta t$ liter klorhaltigt vatten. Om $\Delta t$ är litet, så är $y(t)$ nästan konstant under tiden och mängden klor i läckagevattnet är ungefär $300y(t)\Delta t$ liter, så <math>
 +y(t+\Delta t)\approx\frac{300000y(t)-300y(t)\Delta t}{300000}=y(t)-0,001y(t)\Delta t,</math>
 +vilket ger <math>
 +\frac{y(t+\Delta t)-y(t)}{\Delta t}\approx -0,001y(t).</math>
 +Låter vi $\Delta t\to 0$ så får vi DE:n $y'(t)=-0,001y(t)$, som har lösningen $y(t)=Ce^{-0,001t}$. Då $t=0$ är klorhalten $y(0)=C=1/300000$, så <math>
 +y(t)=\frac{e^{-0,001t}}{300000}.</math>
 +Beteckna tidpunkten då halten är 1 ppm med $T$. Då får vi ekvationen <math>
 +\frac{e^{-0,001T}}{300000}=10^{-6},</math>
 +som ger <math>
 +T=\frac{\ln (3\cdot 10^5\cdot 10^{-6})}{-0,001}=\frac{\ln 0,3}{-0,001}\approx 1200\quad\mbox{dygn.}</math>
 +
 +
 +
 +'''13.40.a.'''
 +
 +DE:n är <math>
 +\frac{dp}{dt}=0,04p-0,0004p^2-1.</math>
 +
 +
 +'''13.40.b.'''
 +
 +DE:n har separabla variabler: <math>
 +\frac{1}{0,04p-0,0004p^2-1}\, \frac{dp}{dt}=1.</math>
 +Vi skriver om den som <math>
 +\frac{1}{p^2-100p+2500}\, \frac{dp}{dt}=-0,0004</math>
 +och måste hitta en primitiv funktion till den rationella funktionen i VL. Det råkar vara ganska enkelt: <math>
 +\int\frac{dp}{p^2-100p+2500}=\int\frac{dp}{(p-50)^2}=-\frac{1}{p-50}+C.</math>
 +Alltså är <math>
 +-\frac{1}{p-50}+C=-0,0004t.</math>
 +Vi har $p(0)=10000$, så $C=1/(10000-50)$, varav <math>
 +p(t)=50+\frac{9950}{3,98t+1}=\frac{199t+10000}{3,98t+1}.</math>
 +(Här är det fel i bokens facit; 2000 i täljaren måste vara 10000, annars stämmer inte antalet fiskar vid $t=0$.) När $t\to\infty$ så går detta mot 50.
 +
[[Exempellösningar|Tillbaka till lösningarna]] [[Exempellösningar|Tillbaka till lösningarna]]

Versionen från 26 oktober 2007 kl. 10.55

Lösningar till några övningar till lektion 21

13.12.

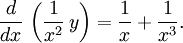Skriv ekvationen som \begin{array} y'-\frac{2}{x}\, y=x+\frac{1}{x}.\end{array} En primitiv funktion till $-2/x$ är $-2\ln x$ (observera att $x>0$), så en integrerande faktor är $e^{-2\ln x}=x^{-2}=1/x^2$. Multiplicerar vi (1) med den så får vi \frac{1}{x^2}\, y'-\frac{2}{x^3}\, y=\frac{1}{x}+\frac{1}{x^3} som kan skrivas \frac{d}{dx}\,\left(\frac{1}{x^2}\, y\right)=\frac{1}{x}+\frac{1}{x^3}. 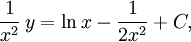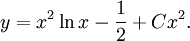Alltså är \frac{1}{x^2}\, y=\ln x-\frac{1}{2x^2}+C, där $C$ är en konstant, eller y=x^2\ln x-\frac{1}{2}+Cx^2. Villkoret $y(1)=0$ ger $-1/2+C=0$, dvs $C=1/2$, så den sökta lösningen är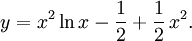 y=x^2\ln x-\frac{1}{2}+\frac{1}{2}\,x^2.


13.13.

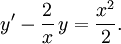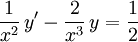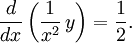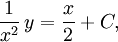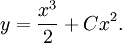Ekvationen kan skrivas y'-\frac{2}{x}\, y=\frac{x^2}{2}. En primitiv funktion till $-2/x$ är $-2\ln x$ (ty $x>0$), så en integrerande faktor är $e^{-2\ln x}=1/x^2$. Multiplicerar vi med den så får vi \frac{1}{x^2}\, y'-\frac{2}{x^3}\, y=\frac{1}{2} som kan skrivas \frac{d}{dx}\left(\frac{1}{x^2}\, y\right)=\frac{1}{2}. Alltså är \frac{1}{x^2}\, y=\frac{x}{2}+C, där $C$ är en konstant, eller y=\frac{x^3}{2}+Cx^2. Villkoret $y(1)=0$ ger $1/2+C=0$, så $C=-1/2$ och den sökta lösningen är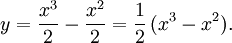 y=\frac{x^3}{2}-\frac{x^2}{2}=\frac{1}{2}\,(x^3-x^2).


13.15.

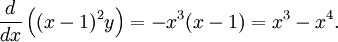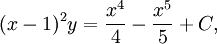Vi skriver ekvationen som y'+\frac{2}{x-1}\, y=-\frac{x^3}{x-1}. En primitiv funktion till $2/(x-1)$ är $2\ln(x-1)$ (observera att $x>1$), så en integrerande faktor är $e^{2\ln(x-1)}=(x-1)^2$. Multiplicerar vi med den så får vi (x − 1)2y' + 2(x − 1)y = − x3(x − 1), som kan skrivas \frac{d}{dx}\left((x-1)^2y\right)=-x^3(x-1)=x^3-x^4. 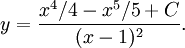Alltså är (x-1)^2y=\frac{x^4}{4}-\frac{x^5}{5}+C, där $C$ är en konstant, varav y=\frac{x^4/4-x^5/5+C}{(x-1)^2}.


13.17.

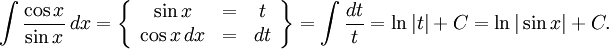Vi skriver ekvationen som y'-\frac{2\cos x}{\sin x}\, y=\frac{\cos x}{\sin x} och måste hitta en primitiv funktion till $-2\cos x/\sin x$. En substitution löser problemet:\int\frac{\cos x}{\sin x}\, dx=\left\{\begin{array}{ccccc} \sin x&=&t\\ \cos x\, dx&=&dt\end{array}\right\}= \int\frac{dt}{t}=\ln |t|+C=\ln|\sin x|+C. Vi väljer den primitiva funktionen $-2\ln|\sin x|$ och får den integrerande faktorn e^{-2\ln|\sin x|}=(|\sin x|)^{-2}=\frac{1}{\sin^2x}. 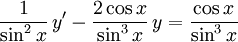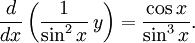Multiplicerar vi med den så får vi \frac{1}{\sin^2x}\, y'-\frac{2\cos x}{\sin^3x}\, y=\frac{\cos x}{\sin^3x} som kan skrivas \frac{d}{dx}\left(\frac{1}{\sin^2x}\, y\right)=\frac{\cos x}{\sin^3x}. Med samma substitution som nyss så får vi att $-1/2\sin^2x+C$ är de primitiva funktionerna till HL, varför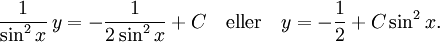 \frac{1}{\sin^2x}\, y=-\frac{1}{2\sin^2x}+C\quad\mbox{eller}\quad y=-\frac{1}{2}+C\sin^2x.


13.19.

Beteckna klorhalten vid tiden $t$ dygn med $y(t)$ (mätt som liter klor per liter klorhaltigt vatten i cisternen). Mellan tidpunkterna $t$ och $t+\Delta t$ läcker $300\Delta t$ liter klorhaltigt vatten. 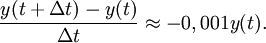Om $\Delta t$ är litet, så är $y(t)$ nästan konstant under tiden och mängden klor i läckagevattnet är ungefär $300y(t)\Delta t$ liter, så y(t+\Delta t)\approx\frac{300000y(t)-300y(t)\Delta t}{300000}=y(t)-0,001y(t)\Delta t, vilket ger \frac{y(t+\Delta t)-y(t)}{\Delta t}\approx -0,001y(t). Låter vi $\Delta t\to 0$ så får vi DE:n $y'(t)=-0,001y(t)$, som har lösningen $y(t)=Ce^{-0,001t}$. Då $t=0$ är klorhalten $y(0)=C=1/300000$, så 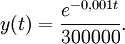y(t)=\frac{e^{-0,001t}}{300000}. Beteckna tidpunkten då halten är 1 ppm med $T$. Då får vi ekvationen 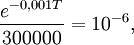\frac{e^{-0,001T}}{300000}=10^{-6}, som ger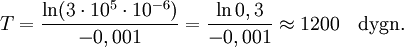 T=\frac{\ln (3\cdot 10^5\cdot 10^{-6})}{-0,001}=\frac{\ln 0,3}{-0,001}\approx 1200\quad\mbox{dygn.}


13.40.a.

DE:n är 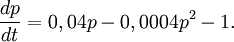\frac{dp}{dt}=0,04p-0,0004p^2-1.


13.40.b.

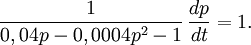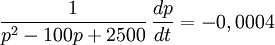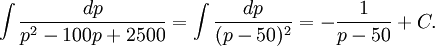DE:n har separabla variabler: \frac{1}{0,04p-0,0004p^2-1}\, \frac{dp}{dt}=1. Vi skriver om den som \frac{1}{p^2-100p+2500}\, \frac{dp}{dt}=-0,0004 och måste hitta en primitiv funktion till den rationella funktionen i VL. Det råkar vara ganska enkelt: \int\frac{dp}{p^2-100p+2500}=\int\frac{dp}{(p-50)^2}=-\frac{1}{p-50}+C. Alltså är -\frac{1}{p-50}+C=-0,0004t. Vi har $p(0)=10000$, så $C=1/(10000-50)$, varav p(t)=50+\frac{9950}{3,98t+1}=\frac{199t+10000}{3,98t+1}. (Här är det fel i bokens facit; 2000 i täljaren måste vara 10000, annars stämmer inte antalet fiskar vid $t=0$.) När $t\to\infty$ så går detta mot 50.


Tillbaka till lösningarna

Den här artikeln är hämtad från http://wiki.math.se/wikis/mm1001_0701/index.php/L%C3%B6sningar_21
Personliga verktyg