Lösningar 15

Matematik för naturvetare 15hp

(Skillnad mellan versioner)

Hoppa till: navigering, sök

Versionen från 16 oktober 2007 kl. 13.16

Lösningar till några övningar till lektion 15

Tillbaka till lösningarna

7.8.

Derivatan av $v(r)=K(Rr^2-r^3)$ är

$v'(r) = K (2 R r - 3 r 2) = K r (2 R - 3 r)$

som har två nollställen $r=0$ och $r=2R/3$. Teckenväxlingen vid det senare är $+0-$ och det är alltså ett lokalt maximum. Vi har $v(0)=v(R)=0$, $v(2R/3)=4KR^3/27$, så det största värdet är $4KR^3/27$.

7.9.

iguren nedan föreställer ett tvärsnitt genom sfären och cylindern. Enligt Pythagoras sats gäller sambandet $r^2+(h/2)^2=R^2$ mellan radien $r$ och höjden $h$ i cylindern. Dess volym är

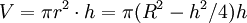
$V=\pi{}r^2\cdot h=\pi{}(R^2-h^2/4)h$

Derivatan är

$V'(h) = π(R 2 - 3 h 2 / 4)$

med ett positivt nollställe $h=2R/\sqrt 3$. Eftersom $V(0)=V(2R)=0$ så måste detta vara ett lokalt maximum och ge $V$:s största värde. Det blir

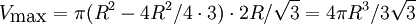
$V_{\mbox{max}}=\pi{}(R^2-4R^2/4\cdot 3)\cdot 2R/\sqrt 3=4\pi{}R^3/3\sqrt 3$

7.10.

Självklart kan man derivera osv, men det är mer upplysande att kvadratkomplettera:

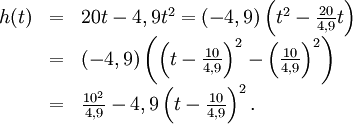
$\begin{array}{lll} h(t)&=&20t-4,9t^2=(-4,9)\left(t^2-\frac{20}{4,9}t\right)\\ &=& (-4,9)\left(\left(t-\frac{10}{4,9}\right)^2-\left(\frac{10}{4,9}\right)^2\right)\\ &=& \frac{10^2}{4,9}-4,9\left(t-\frac{10}{4,9}\right)^2.\end{array}$

Här ser vi att $h$:s största värde är $100/4,9\approx 20,4$ meter och att det antas vid tiden $t=10/4,9\approx 2$ sekunder.

7.11.a) Gränsvärdet

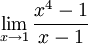
$\lim_{x\to 1}\frac{x^4-1}{x-1}$

är derivatan av $y=x^4$ för $x=1$, dvs $4\cdot 1^3=4$. Det sökta gränsvärdet är således $1/4$.

b) \begin{array} \lim_{x\to 0}\frac{\tan 2x}{\sin x}&=&\lim_{x\to 0}\frac{\sin 2x}{\cos 2x\sin x}=\lim_{x\to 0}\frac{2\sin x\cos x}{\cos 2x\sin x}= \lim_{x\to 0}\frac{2\cos x}{\cos 2x}\\ &=&\frac{2\cos 0}{\cos 0}=2\end{array}

c) Eftersom nämnaren är $\not=0$ för $x=0$ så kan man helt enkelt sätta in $x=0$. Gränsvärdet är således $(0-1)/1=-1$.

d) Sätt $x=\tan t$, alltså $t=\arctan x$. När $x\to 0$ så har vi $t\to 0$, så

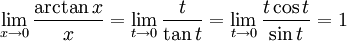
$\lim_{x\to 0}\frac{\arctan x}{x}=\lim_{t\to 0}\frac{t}{\tan t}= \lim_{t\to 0}\frac{t\cos t}{\sin t}=1$

eftersom $\lim_{t\to 0}((\sin t)/t)=1$. Man kan alternativt uppfatta gränsvärdet som derivatan av $\arctan x$ för $x=0$, dvs skriva

$\lim_{x\to 0}\frac{\arctan x}{x}=\lim_{x\to 0}\frac{\arctan x-\arctan 0}{x-0}.$

Gränsvärdet är alltså $1/(1+0^2)=1$.

e) Det här gränsvärdet är kvadraten på det i d), dvs också 1.

f) Sätt $t=x-\pi{}/2$, så att $t\to 0$ då $x\to \pi{}/2$. Vi har

$cos(x - π) = cos(t + π / 2 - π) = cos(t - π / 2) = cos(π / 2 - t) = sin t,$

så

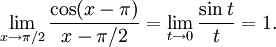
$\lim_{x\to \pi{}/2}\frac{\cos(x-\pi{})}{x-\pi{}/2}=\lim_{t\to 0}\frac{\sin t}{t}=1.$

7.12.l'Hospital ger att gränsvärdet är lika med

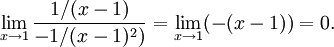$\lim_{x\to 1}\frac{1/(x-1)}{-1/(x-1)^2)}=\lim_{x\to 1}(-(x-1))=0.$ Ett enklare sätt att beräkna det är att skriva det som

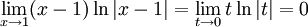
$\lim_{x\to 1}(x-1)\ln|x-1|=\lim_{t\to 0}t\ln|t|=0$

enligt standardgränsvärdena.

7.13.Vi har

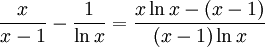
$\frac{x}{x-1}-\frac{1}{\ln x}=\frac{x\ln x-(x-1)}{(x-1)\ln x}$

och när $x\to 1$ så går både täljare och nämnare mot 0, så vi kan använda l'Hospital. Derivatan av täljaren är $\ln x+1-1=\ln x$ och av nämmnaren $\ln x+(x-1)/x$. Vi har

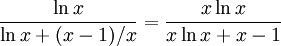
$\frac{\ln x}{\ln x+(x-1)/x}=\frac{x\ln x}{x\ln x+x-1}$

och även här är täljare och nämnare 0 för $x=1$. Vi använder l'Hospital igen. Derivatan av täljaren är $\ln x+1$ och av nämnaren $\ln x+1+1=\ln x+2$. Gränsvärdet är alltså lika med

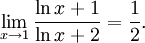
$\lim_{x\to 1}\frac{\ln x+1}{\ln x+2}=\frac{1}{2}.$

Har man läst om Maclaurinpolynom, så kan man beräkna gränsvärdet på ett annat sätt också. Sätter vi $t=x-1$ så är uttrycket lika med

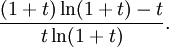
$\frac{(1+t)\ln(1+t)-t}{t\ln(1+t)}.$

Notera att $t\to 0$ då $x\to 1$. Enligt Taylors sats är $\ln(1+t)=t-t^2/2+t^3B(t)$, där $B$ är en funktion som är begränsad nära 0. Insättning och lite förenklingsarbete ger att det här är lika med

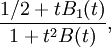
$\frac{1/2+tB_{1}(t)}{1+t^2B(t)},$

där även $B_{1}$ är begränsad nära 0. Gränsvärdet är således 1/2.

7.14.

Kvadratkomplettering ger

Misslyckades med att tolka formel. (okänt fel): \begin{array} P(I)&=&-R\left( I^2-\frac{U}{R}I\right)=-R\left(\left(I-\frac{U}{2R}\right)^2- \left(\frac{U}{2R}\right)^2\right)\\ &=& \frac{U^2}{4R}-R\left(I-\frac{U}{2R}\right)^2\end{array}

Det största värdet är alltså $U^2/4R$, vilket antas för $I=U/2R$.

7.15.

Här är det lämpligt att skriva om uttrycket för $H$ innan man börjar derivera. Sätt $x=e^{-0,1t}$. Då är

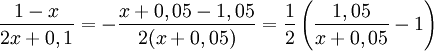$\frac{1-x}{2x+0,1}=-\frac{x+0,05-1,05}{2(x+0,05)}= \frac{1}{2}\left(\frac{1,05}{x+0,05}-1\right)$ och alltså

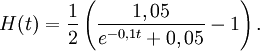
$H(t)=\frac{1}{2}\left(\frac{1,05}{e^{-0,1t}+0,05}-1\right).$

Derivatan är

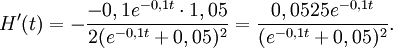
$H'(t)=-\frac{-0,1e^{-0,1t}\cdot 1,05}{2(e^{-0,1t}+0,05)^2}= \frac{0,0525e^{-0,1t}}{(e^{-0,1t}+0,05)^2}.$

Nu är

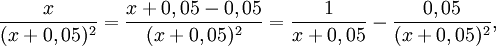
$\frac{x}{(x+0,05)^2}=\frac{x+0,05-0,05}{(x+0,05)^2}=\frac{1}{x+0,05}- \frac{0,05}{(x+0,05)^2},$

alltså

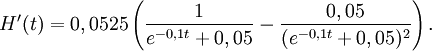
$H'(t)=0,0525\left(\frac{1}{e^{-0,1t}+0,05}-\frac{0,05}{(e^{-0,1t}+0,05)^2}\right).$

Vi skall bestämma det värde på $t$ för vilket $H'(t)$ är störst och deriverar:

Misslyckades med att tolka formel. (okänt fel): \begin{array} H''(t)&=&0,0525\left(-\frac{-0,1e^{-0,1t}}{(e^{-0,1t}+0,05)^2}+ \frac{2\cdot 0,05\cdot (-0,1e^{-0,1t})}{(e^{-0,1t}+0,05)^3}\right)\\ &=& \frac{0,00525e^{-0,1t}(e^{-0,1t}-0,05)}{(e^{-0,1t}+0,05)^3}\end{array}

$H$ har ett nollställe som ges av ekvationen $e^{-0,1t}=0,05$ och teckenväxlingen är $+0-$, så detta är ett lokalt maximum, som också måste vara $H'$:s största värde. Vi får $t=(\ln 0,05)/(-0,1)\approx 30$ dagar.

Eftersom $H'(t)>0$, så är $H(t)$ strängt växande och solrosens maximala höjd nås då $t\to\infty$. Den är $34/0,1=340$ cm.

8.2.

Om man byter $x$ mot $2x$ i Maclaurinserien för $e^x$ så får man

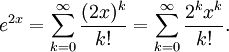
$e^{2x}=\sum_{k=0}^{\infty}\frac{(2x)^k}{k!}= \sum_{k=0}^{\infty}\frac{2^kx^k}{k!}.$

8.4.a)

Derivatorna är

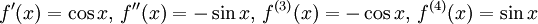
$f'(x)=\cos x,\, f''(x)=-\sin x,\, f^{(3)}(x)=-\cos x,\, f^{(4)}(x)=\sin x$

och värdena för $x=\pi{}/4$

Misslyckades med att tolka formel. (okänt fel): \begin{array} f(\pi{}/4)&=&1/\sqrt 2,\, f'(\pi{}/4)=1/\sqrt 2,\, f''(\pi{}/4)=-1/\sqrt 2, \\ f^{(3)}(\pi{}/4)&=&-1/\sqrt 2,\, f^{(4)}(\pi{}/4)=1/\sqrt 2.\end{array}

Taylorpolynomet är således

Misslyckades med att tolka formel. (okänt fel): \begin{array} p_{\pi{}/4,4}(x)&=&f(\pi{}/4)+f'(\pi{}/4)(x-\pi{}/4)+\frac{f''(\pi{}/4)}{2}(x-\pi{}/4)^2\\&+& \frac{f^{(3)}(\pi{}/4)}{3!}(x-\pi{}/4)^3 +\frac{f^{(4)}(\pi{}/4)}{4!}(x-\pi{}/4)^4\\ &=& \frac{1}{\sqrt 2}\left(1+(x-\pi{}/4)-\frac{(x-\pi{}/4)^2}{2}-\frac{(x-\pi{}/4)^3}{6}+ \frac{(x-\pi{}/4)^4}{24}\right).\end{array}

b) Det är lätt att beräkna derivatorna om man skriver $\sqrt{1+x}=(1+x)^{1/2}$:

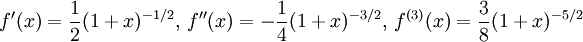
$f'(x)=\frac{1}{2}(1+x)^{-1/2},\, f''(x)=-\frac{1}{4}(1+x)^{-3/2},\, f^{(3)}(x)=\frac{3}{8}(1+x)^{-5/2}$

Alltså är

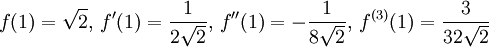
$f(1)=\sqrt 2, \, f'(1)=\frac{1}{2\sqrt 2},\, f''(1)=-\frac{1}{8\sqrt 2},\, f^{(3)}(1)=\frac{3}{32\sqrt 2}$

så att Taylorpolynomet är

Misslyckades med att tolka formel. (okänt fel): \begin{array} p_{1,3}(x)&=&f(1)+f'(1)(x-1)+\frac{f''(1)}{2}(x-1)^2+ \frac{f^{(3)}(1)}{3!}(x-1)^3\\ &=& \sqrt 2\left(1+\frac{1}{4}(x-1)-\frac{1}{32}(x-1)^2+\frac{1}{128}(x-1)^3\right). \end{array}

8.5.a)

Maclaurinpolynomet är

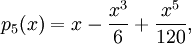
$p_{5}(x)=x-\frac{x^3}{6}+\frac{x^5}{120},$

så

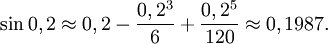
$\sin 0,2\approx 0,2-\frac{0,2^3}{6}+\frac{0,2^5}{120}\approx 0,1987.$

c) Maclaurinpolynomet är

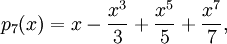
$p_{7}(x)=x-\frac{x^3}{3}+\frac{x^5}{5}+\frac{x^7}{7},$

så

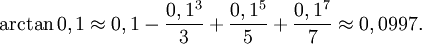
$\arctan 0,1\approx 0,1-\frac{0,1^3}{3}+\frac{0,1^5}{5}+\frac{0,1^7}{7} \approx 0,0997.$

8.9.Eftersom nämnaren har grad 3, så försöker vi med att utvecka arctan och sin t o m ordning 3:

$\arctan 2x=2x-\frac{(2x)^3}{3}+x^5B(x),\quad \sin 2x=2x-\frac{(2x)^3}{6}+x^5C(x),$

där $B$ och $C$ är begränsade nära 0. Alltså är

Misslyckades med att tolka formel. (okänt fel): \begin{array} \frac{\arctan 2x-\sin 2x}{x^3}&=&\frac{-8x^3/3+8x^3/6+x^5(B(x)-C(x))}{x^3}\\ &=& -4/3+x^2(B(x)-C(x)).\end{array}

Eftersom $B-C$ är begränsad nära 0, så går $x^2(B(x)-C(x))$ mot 0 då $x\to 0$, och gränsvärdet är därför $-4/3$.

8.10.

Vi har för det första $f(x)=\cos x\cdot\ln(1+x)$ och för det andra

Misslyckades med att tolka formel. (okänt fel): \begin{array} \cos x&=&1-\frac{x^2}{2}+x^4B(x)\\ \ln(1+x)&=&x-\frac{x^2}{2}+\frac{x^3}{3}+x^4C(x)\end{eqnarray*}

där $B,C$ är begränsade nära 0 (för att säkert få alla termer av ordning $\le 3$ måste vi ta med alla termer av grad $\le 3$ i de två inblandade funktionerna). Alltså är

Misslyckades med att tolka formel. (okänt fel): \begin{array} f(x)&=&\left(1-\frac{x^2}{2}+x^4B(x)\right)\left( x-\frac{x^2}{2}+\frac{x^3}{3}+x^4C(x)\right)\\ &=& x-\frac{x^2}{2}-\frac{x^3}{6}+x^4D(x),\end{array}

där $D$ är en kombination av $B$ och $C$ och begränsad nära 0. Tydligen är

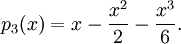
$p_{3}(x)=x-\frac{x^2}{2}-\frac{x^3}{6}.$

Det går naturligtvis bra att derivera $f$ direkt också.

8.11.

Använd först additionsformeln:

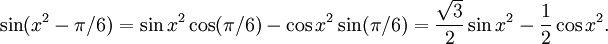
$\sin(x^2-\pi{}/6)=\sin x^2\cos (\pi{}/6)-\cos x^2\sin (\pi{}/6)= \frac{\sqrt 3}{2}\sin x^2-\frac{1}{2}\cos x^2.$

Nu är ju

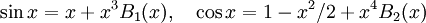
$\sin x=x+x^3B_{1}(x),\quad \cos x=1-x^2/2+x^4B_{2}(x)$

där $B_{1}$ och $B_{2}$ är begränsade nära 0. Alltså är

Misslyckades med att tolka formel. (okänt fel): \begin{array} \sin(x^2-\pi{}/6)&=&\frac{\sqrt 3}{2}(x^2+x^{6}B_{1}(x^2))- \frac{1}{2}(1-x^4/2+x^8B_{2}(x^2))\\ &=& -\frac{1}{2}+\frac{\sqrt 3}{2}\, x^2+\frac{1}{4}\, x^4+x^6B(x),\end{array}

där $B(x)=(\sqrt 3/2)B_{1}(x)-(1/2)x^2B_{2}(x)$ är begränsad nära 0. Maclaurinpolynomet med tre termer är således

$-\frac{1}{2}+\frac{\sqrt 3}{2}\, x^2+\frac{1}{4}\, x^4.$

Man skulle kanske gärna vilja använda Maclaurinserien för sinus i den här uppgiften, dvs i

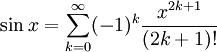
$\sin x=\sum_{k=0}^{\infty}(-1)^k\frac{x^{2k+1}}{(2k+1)!}$

ersätta $x$ med $x^2-\pi{}/6$, och det kan man göra, eftersom serien framställer $\sin x$ för alla $x$, men då måste man tänka noga på vad man gör. Vi får

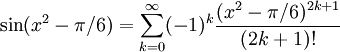
$\sin(x^2-\pi{}/6)=\sum_{k=0}^{\infty}(-1)^k\frac{(x^2-\pi{}/6)^{2k+1}}{(2k+1)!}$

och här måste vi utveckla alla $(x^2-\pi{}/6)^{2k+1}$ för att få Maclaurinserien. Problemet som uppstår är att {\it varje term} $(x^2-\pi{}/6)^{2k+1}$ ger bidrag till de tre första termerna (i själva verket till alla termer av grad $\le 2k+1$). Den konstanta termen blir

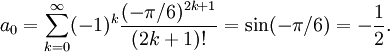
$a_{0}=\sum_{k=0}^{\infty}(-1)^k\frac{(-\pi{}/6)^{2k+1}}{(2k+1)!}=\sin(-\pi{}/6)=-\frac{1}{2}.$

Enligt binomialsatsen är

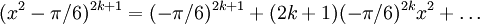
$(x^2-\pi{}/6)^{2k+1}=(-\pi{}/6)^{2k+1}+(2k+1)(-\pi{}/6)^{2k}x^2+\ldots$

där prickarna betyder termer av högre grad. Koefficienten för $x^2$-termen i Mac\-laurinserien är således

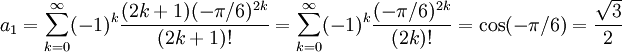
$a_{1}=\sum_{k=0}^{\infty}(-1)^k\frac{(2k+1)(-\pi{}/6)^{2k}}{(2k+1)!}= \sum_{k=0}^{\infty}(-1)^{k}\frac{(-\pi{}/6)^{2k}}{(2k)!}=\cos(-\pi{}/6)=\frac{\sqrt 3}{2}$

Bestäm nästa term själv!

Den här artikeln är hämtad från http://wiki.math.se/wikis/mm1001_0701/index.php/L%C3%B6sningar_15

+[[Bild: Fig3dag15.jpg]]
-\begin{center}
-\includegraphics[0mm,0mm][10cm,10cm]{Fig3dag15.jpg}\end{center}

Lösningar 15

Matematik för naturvetare 15hp

Versionen från 16 oktober 2007 kl. 13.16

Lösningar till några övningar till lektion 15

Visningar

Personliga verktyg

Navigering

Sök

Verktygslåda