Lösningar 15

Matematik för naturvetare 15hp

(Skillnad mellan versioner)

Hoppa till: navigering, sök

Versionen från 16 oktober 2007 kl. 13.26

Lösningar till några övningar till lektion 15

Tillbaka till lösningarna

7.8.

Derivatan av $v(r)=K(Rr^2-r^3)$ är

$v'(r) = K (2 R r - 3 r 2) = K r (2 R - 3 r)$

som har två nollställen $r=0$ och $r=2R/3$. Teckenväxlingen vid det senare är $+0-$ och det är alltså ett lokalt maximum. Vi har $v(0)=v(R)=0$, $v(2R/3)=4KR^3/27$, så det största värdet är $4KR^3/27$.

7.9.

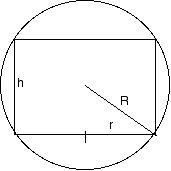
Figuren nedan föreställer ett tvärsnitt genom sfären och cylindern. Enligt Pythagoras sats gäller sambandet $r^2+(h/2)^2=R^2$ mellan radien $r$ och höjden $h$ i cylindern. Dess volym är

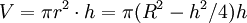
$V=\pi{}r^2\cdot h=\pi{}(R^2-h^2/4)h$

Derivatan är

$V'(h) = π(R 2 - 3 h 2 / 4)$

med ett positivt nollställe $h=2R/\sqrt 3$. Eftersom $V(0)=V(2R)=0$ så måste detta vara ett lokalt maximum och ge $V$:s största värde. Det blir

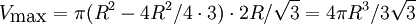
$V_{\mbox{max}}=\pi{}(R^2-4R^2/4\cdot 3)\cdot 2R/\sqrt 3=4\pi{}R^3/3\sqrt 3$

7.10.

Självklart kan man derivera osv, men det är mer upplysande att kvadratkomplettera:

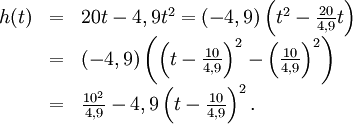
$\begin{array}{lll} h(t)&=&20t-4,9t^2=(-4,9)\left(t^2-\frac{20}{4,9}t\right)\\ &=& (-4,9)\left(\left(t-\frac{10}{4,9}\right)^2-\left(\frac{10}{4,9}\right)^2\right)\\ &=& \frac{10^2}{4,9}-4,9\left(t-\frac{10}{4,9}\right)^2.\end{array}$

Här ser vi att $h$:s största värde är $100/4,9\approx 20,4$ meter och att det antas vid tiden $t=10/4,9\approx 2$ sekunder.

7.11.a)

Gränsvärdet

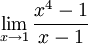
$\lim_{x\to 1}\frac{x^4-1}{x-1}$

är derivatan av $y=x^4$ för $x=1$, dvs $4\cdot 1^3=4$. Det sökta gränsvärdet är således $1/4$.

7.11.b)

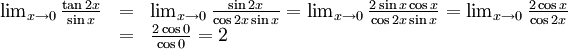
$\begin{array}{lll} \lim_{x\to 0}\frac{\tan 2x}{\sin x}&=&\lim_{x\to 0}\frac{\sin 2x}{\cos 2x\sin x}=\lim_{x\to 0}\frac{2\sin x\cos x}{\cos 2x\sin x}= \lim_{x\to 0}\frac{2\cos x}{\cos 2x}\\ &=&\frac{2\cos 0}{\cos 0}=2\end{array}$

7.11.c)

Eftersom nämnaren är $\not=0$ för $x=0$ så kan man helt enkelt sätta in $x=0$. Gränsvärdet är således $(0-1)/1=-1$.

7.11.d)

Sätt $x=\tan t$, alltså $t=\arctan x$. När $x\to 0$ så har vi $t\to 0$, så

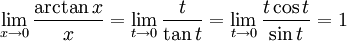
$\lim_{x\to 0}\frac{\arctan x}{x}=\lim_{t\to 0}\frac{t}{\tan t}= \lim_{t\to 0}\frac{t\cos t}{\sin t}=1$

eftersom $\lim_{t\to 0}((\sin t)/t)=1$. Man kan alternativt uppfatta gränsvärdet som derivatan av $\arctan x$ för $x=0$, dvs skriva

$\lim_{x\to 0}\frac{\arctan x}{x}=\lim_{x\to 0}\frac{\arctan x-\arctan 0}{x-0}$

Gränsvärdet är alltså $1/(1+0^2)=1$.

7.11.e)

Det här gränsvärdet är kvadraten på det i d), dvs också 1.

7.11.f)

Sätt $t=x-\pi{}/2$, så att $t\to 0$ då $x\to \pi{}/2$. Vi har

$cos(x - π) = cos(t + π / 2 - π) = cos(t - π / 2) = cos(π / 2 - t) = sin t$

så

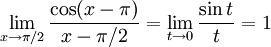
$\lim_{x\to \pi{}/2}\frac{\cos(x-\pi{})}{x-\pi{}/2}=\lim_{t\to 0}\frac{\sin t}{t}=1$

7.12.

l'Hospital ger att gränsvärdet är lika med

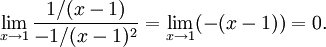
$\lim_{x\to 1}\frac{1/(x-1)}{-1/(x-1)^2}=\lim_{x\to 1}(-(x-1))=0.$

Ett enklare sätt att beräkna det är att skriva det som

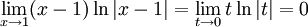
$\lim_{x\to 1}(x-1)\ln|x-1|=\lim_{t\to 0}t\ln|t|=0$

enligt standardgränsvärdena.

7.13.

Vi har

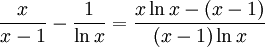
$\frac{x}{x-1}-\frac{1}{\ln x}=\frac{x\ln x-(x-1)}{(x-1)\ln x}$

och när $x\to 1$ så går både täljare och nämnare mot 0, så vi kan använda l'Hospital. Derivatan av täljaren är $\ln x+1-1=\ln x$ och av nämmnaren $\ln x+(x-1)/x$. Vi har

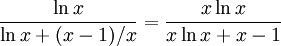
$\frac{\ln x}{\ln x+(x-1)/x}=\frac{x\ln x}{x\ln x+x-1}$

och även här är täljare och nämnare 0 för $x=1$. Vi använder l'Hospital igen. Derivatan av täljaren är $\ln x+1$ och av nämnaren $\ln x+1+1=\ln x+2$. Gränsvärdet är alltså lika med

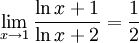
$\lim_{x\to 1}\frac{\ln x+1}{\ln x+2}=\frac{1}{2}$

Har man läst om Maclaurinpolynom, så kan man beräkna gränsvärdet på ett annat sätt också. Sätter vi $t=x-1$ så är uttrycket lika med

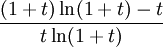
$\frac{(1+t)\ln(1+t)-t}{t\ln(1+t)}$

Notera att $t\to 0$ då $x\to 1$. Enligt Taylors sats är $\ln(1+t)=t-t^2/2+t^3B(t)$, där $B$ är en funktion som är begränsad nära 0. Insättning och lite förenklingsarbete ger att det här är lika med

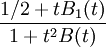
$\frac{1/2+tB_{1}(t)}{1+t^2B(t)}$

där även $B_{1}$ är begränsad nära 0. Gränsvärdet är således 1/2.

7.14.

Kvadratkomplettering ger

$\begin{array}{lll} P(I)&=&-R\left( I^2-\frac{U}{R}I\right)=-R\left(\left(I-\frac{U}{2R}\right)^2- \left(\frac{U}{2R}\right)^2\right)\\ &=& \frac{U^2}{4R}-R\left(I-\frac{U}{2R}\right)^2\end{array}$

Det största värdet är alltså $U^2/4R$, vilket antas för $I=U/2R$.

7.15.

Här är det lämpligt att skriva om uttrycket för $H$ innan man börjar derivera. Sätt $x=e^{-0,1t}$. Då är

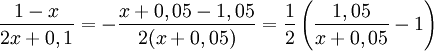$\frac{1-x}{2x+0,1}=-\frac{x+0,05-1,05}{2(x+0,05)}= \frac{1}{2}\left(\frac{1,05}{x+0,05}-1\right)$ och alltså

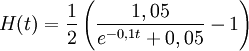
$H(t)=\frac{1}{2}\left(\frac{1,05}{e^{-0,1t}+0,05}-1\right)$

Derivatan är

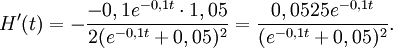
$H'(t)=-\frac{-0,1e^{-0,1t}\cdot 1,05}{2(e^{-0,1t}+0,05)^2}= \frac{0,0525e^{-0,1t}}{(e^{-0,1t}+0,05)^2}.$

Nu är

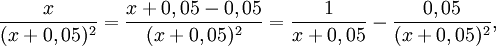
$\frac{x}{(x+0,05)^2}=\frac{x+0,05-0,05}{(x+0,05)^2}=\frac{1}{x+0,05}- \frac{0,05}{(x+0,05)^2},$

alltså

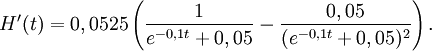
$H'(t)=0,0525\left(\frac{1}{e^{-0,1t}+0,05}-\frac{0,05}{(e^{-0,1t}+0,05)^2}\right).$

Vi skall bestämma det värde på $t$ för vilket $H'(t)$ är störst och deriverar:

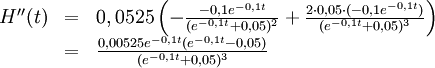
$\begin{array}{lll} H''(t)&=&0,0525\left(-\frac{-0,1e^{-0,1t}}{(e^{-0,1t}+0,05)^2}+ \frac{2\cdot 0,05\cdot (-0,1e^{-0,1t})}{(e^{-0,1t}+0,05)^3}\right)\\ &=& \frac{0,00525e^{-0,1t}(e^{-0,1t}-0,05)}{(e^{-0,1t}+0,05)^3}\end{array}$

$H$ har ett nollställe som ges av ekvationen $e^{-0,1t}=0,05$ och teckenväxlingen är $+0-$, så detta är ett lokalt maximum, som också måste vara $H'$:s största värde. Vi får $t=(\ln 0,05)/(-0,1)\approx 30$ dagar.

Eftersom $H'(t)>0$, så är $H(t)$ strängt växande och solrosens maximala höjd nås då $t\to\infty$. Den är $34/0,1=340$ cm.

8.2.

Om man byter $x$ mot $2x$ i Maclaurinserien för $e^x$ så får man

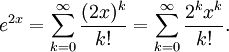
$e^{2x}=\sum_{k=0}^{\infty}\frac{(2x)^k}{k!}= \sum_{k=0}^{\infty}\frac{2^kx^k}{k!}.$

8.4.a)

Derivatorna är

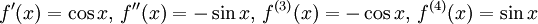
$f'(x)=\cos x,\, f''(x)=-\sin x,\, f^{(3)}(x)=-\cos x,\, f^{(4)}(x)=\sin x$

och värdena för $x=\pi{}/4$

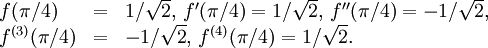
$\begin{array}{lll} f(\pi{}/4)&=&1/\sqrt 2,\, f'(\pi{}/4)=1/\sqrt 2,\, f''(\pi{}/4)=-1/\sqrt 2, \\ f^{(3)}(\pi{}/4)&=&-1/\sqrt 2,\, f^{(4)}(\pi{}/4)=1/\sqrt 2.\end{array}$

Taylorpolynomet är således

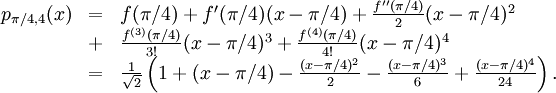
$\begin{array}{lll} p_{\pi{}/4,4}(x)&=&f(\pi{}/4)+f'(\pi{}/4)(x-\pi{}/4)+\frac{f''(\pi{}/4)}{2}(x-\pi{}/4)^2\\&+& \frac{f^{(3)}(\pi{}/4)}{3!}(x-\pi{}/4)^3 +\frac{f^{(4)}(\pi{}/4)}{4!}(x-\pi{}/4)^4\\ &=& \frac{1}{\sqrt 2}\left(1+(x-\pi{}/4)-\frac{(x-\pi{}/4)^2}{2}-\frac{(x-\pi{}/4)^3}{6}+ \frac{(x-\pi{}/4)^4}{24}\right).\end{array}$

b) Det är lätt att beräkna derivatorna om man skriver $\sqrt{1+x}=(1+x)^{1/2}$:

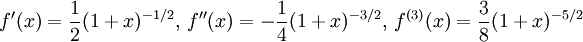
$f'(x)=\frac{1}{2}(1+x)^{-1/2},\, f''(x)=-\frac{1}{4}(1+x)^{-3/2},\, f^{(3)}(x)=\frac{3}{8}(1+x)^{-5/2}$

Alltså är

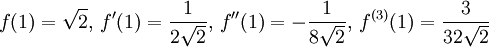
$f(1)=\sqrt 2, \, f'(1)=\frac{1}{2\sqrt 2},\, f''(1)=-\frac{1}{8\sqrt 2},\, f^{(3)}(1)=\frac{3}{32\sqrt 2}$

så att Taylorpolynomet är

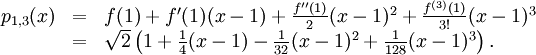
$\begin{array}{lll} p_{1,3}(x)&=&f(1)+f'(1)(x-1)+\frac{f''(1)}{2}(x-1)^2+ \frac{f^{(3)}(1)}{3!}(x-1)^3\\ &=& \sqrt 2\left(1+\frac{1}{4}(x-1)-\frac{1}{32}(x-1)^2+\frac{1}{128}(x-1)^3\right). \end{array}$

8.5.a)

Maclaurinpolynomet är

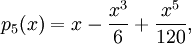
$p_{5}(x)=x-\frac{x^3}{6}+\frac{x^5}{120},$

så

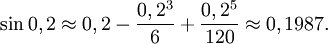
$\sin 0,2\approx 0,2-\frac{0,2^3}{6}+\frac{0,2^5}{120}\approx 0,1987.$

c) Maclaurinpolynomet är

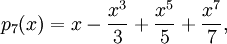
$p_{7}(x)=x-\frac{x^3}{3}+\frac{x^5}{5}+\frac{x^7}{7},$

så

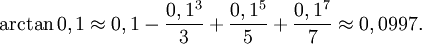
$\arctan 0,1\approx 0,1-\frac{0,1^3}{3}+\frac{0,1^5}{5}+\frac{0,1^7}{7} \approx 0,0997.$

8.9.

Eftersom nämnaren har grad 3, så försöker vi med att utvecka arctan och sin t o m ordning 3:

$\arctan 2x=2x-\frac{(2x)^3}{3}+x^5B(x),\quad \sin 2x=2x-\frac{(2x)^3}{6}+x^5C(x),$

där $B$ och $C$ är begränsade nära 0. Alltså är

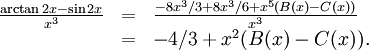
$\begin{array}{lll} \frac{\arctan 2x-\sin 2x}{x^3}&=&\frac{-8x^3/3+8x^3/6+x^5(B(x)-C(x))}{x^3}\\ &=& -4/3+x^2(B(x)-C(x)).\end{array}$

Eftersom $B-C$ är begränsad nära 0, så går $x^2(B(x)-C(x))$ mot 0 då $x\to 0$, och gränsvärdet är därför $-4/3$.

8.10.

Vi har för det första $f(x)=\cos x\cdot\ln(1+x)$ och för det andra

Misslyckades med att tolka formel. (okänt fel): \begin{array}{lll} \cos x&=&1-\frac{x^2}{2}+x^4B(x)\\ \ln(1+x)&=&x-\frac{x^2}{2}+\frac{x^3}{3}+x^4C(x)\end{eqnarray*}

där $B,C$ är begränsade nära 0 (för att säkert få alla termer av ordning $\le 3$ måste vi ta med alla termer av grad $\le 3$ i de två inblandade funktionerna). Alltså är

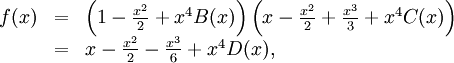
$\begin{array}{lll} f(x)&=&\left(1-\frac{x^2}{2}+x^4B(x)\right)\left( x-\frac{x^2}{2}+\frac{x^3}{3}+x^4C(x)\right)\\ &=& x-\frac{x^2}{2}-\frac{x^3}{6}+x^4D(x),\end{array}$

där $D$ är en kombination av $B$ och $C$ och begränsad nära 0. Tydligen är

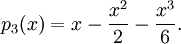
$p_{3}(x)=x-\frac{x^2}{2}-\frac{x^3}{6}.$

Det går naturligtvis bra att derivera $f$ direkt också.

8.11.

Använd först additionsformeln:

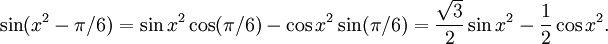
$\sin(x^2-\pi{}/6)=\sin x^2\cos (\pi{}/6)-\cos x^2\sin (\pi{}/6)= \frac{\sqrt 3}{2}\sin x^2-\frac{1}{2}\cos x^2.$

Nu är ju

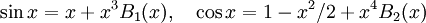
$\sin x=x+x^3B_{1}(x),\quad \cos x=1-x^2/2+x^4B_{2}(x)$

där $B_{1}$ och $B_{2}$ är begränsade nära 0. Alltså är

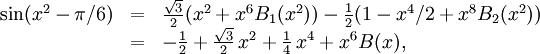
$\begin{array}{lll} \sin(x^2-\pi{}/6)&=&\frac{\sqrt 3}{2}(x^2+x^{6}B_{1}(x^2))- \frac{1}{2}(1-x^4/2+x^8B_{2}(x^2))\\ &=& -\frac{1}{2}+\frac{\sqrt 3}{2}\, x^2+\frac{1}{4}\, x^4+x^6B(x),\end{array}$

där $B(x)=(\sqrt 3/2)B_{1}(x)-(1/2)x^2B_{2}(x)$ är begränsad nära 0. Maclaurinpolynomet med tre termer är således

$-\frac{1}{2}+\frac{\sqrt 3}{2}\, x^2+\frac{1}{4}\, x^4.$

Man skulle kanske gärna vilja använda Maclaurinserien för sinus i den här uppgiften, dvs i

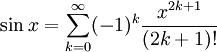
$\sin x=\sum_{k=0}^{\infty}(-1)^k\frac{x^{2k+1}}{(2k+1)!}$

ersätta $x$ med $x^2-\pi{}/6$, och det kan man göra, eftersom serien framställer $\sin x$ för alla $x$, men då måste man tänka noga på vad man gör. Vi får

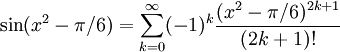
$\sin(x^2-\pi{}/6)=\sum_{k=0}^{\infty}(-1)^k\frac{(x^2-\pi{}/6)^{2k+1}}{(2k+1)!}$

och här måste vi utveckla alla $(x^2-\pi{}/6)^{2k+1}$ för att få Maclaurinserien. Problemet som uppstår är att {\it varje term} $(x^2-\pi{}/6)^{2k+1}$ ger bidrag till de tre första termerna (i själva verket till alla termer av grad $\le 2k+1$). Den konstanta termen blir

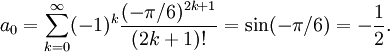
$a_{0}=\sum_{k=0}^{\infty}(-1)^k\frac{(-\pi{}/6)^{2k+1}}{(2k+1)!}=\sin(-\pi{}/6)=-\frac{1}{2}.$

Enligt binomialsatsen är

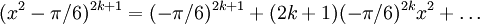
$(x^2-\pi{}/6)^{2k+1}=(-\pi{}/6)^{2k+1}+(2k+1)(-\pi{}/6)^{2k}x^2+\ldots$

där prickarna betyder termer av högre grad. Koefficienten för $x^2$-termen i Mac\-laurinserien är således

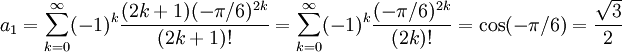
$a_{1}=\sum_{k=0}^{\infty}(-1)^k\frac{(2k+1)(-\pi{}/6)^{2k}}{(2k+1)!}= \sum_{k=0}^{\infty}(-1)^{k}\frac{(-\pi{}/6)^{2k}}{(2k)!}=\cos(-\pi{}/6)=\frac{\sqrt 3}{2}$

Bestäm nästa term själv!

Den här artikeln är hämtad från http://wiki.math.se/wikis/mm1001_0701/index.php/L%C3%B6sningar_15

 <math>
-\lim_{x\to 1}\frac{1/(x-1)}{-1/(x-1)^2)}=\lim_{x\to 1}(-(x-1))=0.</math>
+\lim_{x\to 1}\frac{1/(x-1)}{-1/(x-1)^2}=\lim_{x\to 1}(-(x-1))=0.</math>
 Ett enklare sätt att beräkna det är att skriva det som

Lösningar 15

Matematik för naturvetare 15hp

Versionen från 16 oktober 2007 kl. 13.26

Lösningar till några övningar till lektion 15

Visningar

Personliga verktyg

Navigering

Sök

Verktygslåda