Lektion 8
Matematik för naturvetare 15hp
| Versionen från 23 augusti 2007 kl. 09.54 (redigera) KTH.SE:u17xlk1r (Diskussion | bidrag) (Ny sida: ==Välkommen till Lektion #!== I den här lektionen... Du ska studera följande kapitel i boken: * '''Viktiga saker att tänka på när du läser''' '''Lämpliga övningsuppgifter t...) ← Gå till föregående ändring |
Versionen från 7 september 2007 kl. 11.43 (redigera) (ogör) Clas Löfwall (Diskussion | bidrag) Gå till nästa ändring → |
||
| Rad 1: | Rad 1: | ||
| - | ==Välkommen till Lektion #!== | + | ==Välkommen till Lektion 8!== |
| - | I den här lektionen... | + | [[Läsanvisningar | Tillbaka till läsanvisningarna]] |
| + | |||
| + | |||
| + | I den här lektionen ska vi lära oss vad komplexa tal är för något och hur man räknar med dem och olika sätt att representera dem | ||
| Du ska studera följande kapitel i boken: | Du ska studera följande kapitel i boken: | ||
| - | * | + | * 1.9 De komplexa talen |
| + | * 13.7 Lite mer om komplexa tal | ||
| + | |||
| '''Viktiga saker att tänka på när du läser''' | '''Viktiga saker att tänka på när du läser''' | ||
| + | '''Avsnitt 1.9''' | ||
| + | |||
| + | |||
| + | Lägg märke till att om $z=a+ib$, så är det talet $b$ som är | ||
| + | imaginärdelen, alltså inte $ib$. Både real- och imaginärdelarna av | ||
| + | $z$ är reella tal. Observera också att absolutbeloppet är | ||
| + | $|z|=\sqrt{a^2+b^2}$, inte $\sqrt{a^2+(ib)^2}$. Om $b=0$ så är $z=a$ | ||
| + | ett reellt tal med absolutbelopp $|z|=\sqrt{a^2}=|a|$, där det sista | ||
| + | ledet är det vanliga ''reella'' absolutbeloppet. ''För reella tal | ||
| + | överensstämmer således det komplexa absolutbeloppet med det reella.'' | ||
| + | |||
| + | Med hjälp av Pythagoras sats så ser vi att $|a+ib|=\sqrt{a^2+b^2}$ är avståndet från origo till punkten $a+ib$ (se längst ned på sid 49). | ||
| + | |||
| + | Addition, subtraktion och multiplikation av komplexa tal går till så att man "räknar som vanligt" men kommer ihåg att $i^2=-1$. Det betyder t.ex. att produkten av $a+ib$ och $c+id$ är | ||
| + | |||
| + | $$(a+ib)(c+id)=(ac-bd)+i(ad+bc)$$ | ||
| + | |||
| + | Tillämpar man detta på produkten $z\cdot \overline z$ där $z=a+ib$ så får man $z\cdot \overline z=(a+ib)(a-ib)=a^2+b^2=|z|^2$ (se längst ned på sid 49). | ||
| + | |||
| + | |||
| + | |||
| + | I Exempel 1.31 drar man kvadratroten ur ett negativt tal | ||
| + | $\sqrt{-16}=±4i$. Normalt brukar man dock reservera beteckningen $\sqrt a$ | ||
| + | för reella tal $a\ge 0$, annars är det lätt hänt att beteckningarna | ||
| + | leder en vilse: | ||
| + | |||
| + | <math> | ||
| + | 1=\sqrt{(-1)^2}=\sqrt{(-1)\cdot (-1)}=\sqrt{-1}\cdot\sqrt{-1}=i\cdot | ||
| + | i=-1</math> | ||
| + | |||
| + | Var är felet? | ||
| + | |||
| + | |||
| + | |||
| + | Konjugering och absolutbelopp har vissa viktiga egenskaper som man | ||
| + | ofta har användning av, men som inte diskuteras i avsnittet (se dock övning 1.47). Vi skall | ||
| + | göra det här istället. Låt $z=a+ib$ vara ett komplext tal; dess | ||
| + | konjugat är $\overline{z}=a-ib$, så | ||
| + | |||
| + | $$ | ||
| + | z\cdot\overline{z}=(a+ib)(a-ib)=a^2-(ib^2)=a^2+b^2=|z|^2$$ | ||
| + | |||
| + | |||
| + | Låt $w=c+id$ vara ett annat komplext tal. Då är | ||
| + | |||
| + | <math> | ||
| + | \overline{z+w}=\overline{(a+c)+i(b+d)}=(a+c)-i(b+d)=(a-ib)+(c-id)= | ||
| + | \overline{z}+\overline{w}</math> | ||
| + | |||
| + | |||
| + | dvs ''konjugatet av en summa är lika med summan av konjugaten'' (se övning 1.47 a). | ||
| + | |||
| + | Motsvarande gäller för produkter: | ||
| + | |||
| + | $$ | ||
| + | zw=(a+ib)(c+id)=ac-bd+i(ad+bc),\quad\mbox{så att}\quad | ||
| + | \overline{zw}=ac-bd-i(ad+bc)$$ | ||
| + | |||
| + | |||
| + | Vidare är | ||
| + | |||
| + | $$ | ||
| + | \overline{z}\cdot\overline{w}=(a-ib)(c-id)=ac-bd-i(ad+bc)$$ | ||
| + | |||
| + | |||
| + | Alltså gäller (övning 1.47 b) | ||
| + | |||
| + | $$ | ||
| + | \overline{zw}=\overline{z}\cdot\overline{w}$$ | ||
| + | |||
| + | |||
| + | Av detta följer vidare | ||
| + | |||
| + | $$ | ||
| + | |zw|^2=(zw)\cdot \overline{zw}=z\cdot w\cdot\overline{z}\cdot \overline{w}= | ||
| + | (z\cdot\overline{z})\cdot (w\cdot\overline{w})=|z|^2\cdot |w|^2=(|z|\cdot |w|)^2$$ | ||
| + | |||
| + | |||
| + | och drar vi kvadratroten ur båda ytterleden så får vi | ||
| + | |||
| + | $$ | ||
| + | |zw|=|z|\cdot |w|$$ | ||
| + | |||
| + | |||
| + | Däremot skall man komma ihåg att $|z+w|$ i allmänhet inte är lika | ||
| + | med $|z|+|w|$, utan bara att det gäller | ||
| + | |||
| + | $$ | ||
| + | |z+w|\le |z|+|w|$$ | ||
| + | |||
| + | |||
| + | vilket kallas ''triangelolikheten'' eftersom det kan tolkas som att längden av en sida i en triangel altid är mindre än summan av de övriga två. Beviset hoppar vi över. | ||
| + | |||
| + | |||
| + | '''Avsnitt 13.7''' | ||
| - | '''Lämpliga övningsuppgifter till Lektion #''' | + | '''Lämpliga övningsuppgifter till Lektion 8''' |
| - | Välj bland följande uppgifter i boken: | + | Välj bland följande uppgifter i boken: 1.44 - 1.47, 13.21 - 13.23 |
| [[Läsanvisningar | Tillbaka till läsanvisningarna]] | [[Läsanvisningar | Tillbaka till läsanvisningarna]] | ||
Versionen från 7 september 2007 kl. 11.43
Välkommen till Lektion 8!
Tillbaka till läsanvisningarna
I den här lektionen ska vi lära oss vad komplexa tal är för något och hur man räknar med dem och olika sätt att representera dem
Du ska studera följande kapitel i boken:
- 1.9 De komplexa talen
- 13.7 Lite mer om komplexa tal
Viktiga saker att tänka på när du läser
Avsnitt 1.9
Lägg märke till att om $z=a+ib$, så är det talet $b$ som är
imaginärdelen, alltså inte $ib$. Både real- och imaginärdelarna av
$z$ är reella tal. Observera också att absolutbeloppet är
$|z|=\sqrt{a^2+b^2}$, inte $\sqrt{a^2+(ib)^2}$. Om $b=0$ så är $z=a$
ett reellt tal med absolutbelopp $|z|=\sqrt{a^2}=|a|$, där det sista
ledet är det vanliga reella absolutbeloppet. För reella tal
överensstämmer således det komplexa absolutbeloppet med det reella.
Med hjälp av Pythagoras sats så ser vi att $|a+ib|=\sqrt{a^2+b^2}$ är avståndet från origo till punkten $a+ib$ (se längst ned på sid 49).
Addition, subtraktion och multiplikation av komplexa tal går till så att man "räknar som vanligt" men kommer ihåg att $i^2=-1$. Det betyder t.ex. att produkten av $a+ib$ och $c+id$ är
$$(a+ib)(c+id)=(ac-bd)+i(ad+bc)$$
Tillämpar man detta på produkten $z\cdot \overline z$ där $z=a+ib$ så får man $z\cdot \overline z=(a+ib)(a-ib)=a^2+b^2=|z|^2$ (se längst ned på sid 49).
I Exempel 1.31 drar man kvadratroten ur ett negativt tal $\sqrt{-16}=±4i$. Normalt brukar man dock reservera beteckningen $\sqrt a$ för reella tal $a\ge 0$, annars är det lätt hänt att beteckningarna leder en vilse:
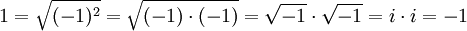
Var är felet?
Konjugering och absolutbelopp har vissa viktiga egenskaper som man ofta har användning av, men som inte diskuteras i avsnittet (se dock övning 1.47). Vi skall göra det här istället. Låt $z=a+ib$ vara ett komplext tal; dess konjugat är $\overline{z}=a-ib$, så
$$ z\cdot\overline{z}=(a+ib)(a-ib)=a^2-(ib^2)=a^2+b^2=|z|^2$$
Låt $w=c+id$ vara ett annat komplext tal. Då är
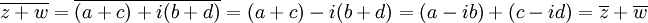
dvs konjugatet av en summa är lika med summan av konjugaten (se övning 1.47 a).
Motsvarande gäller för produkter:
$$ zw=(a+ib)(c+id)=ac-bd+i(ad+bc),\quad\mbox{så att}\quad \overline{zw}=ac-bd-i(ad+bc)$$
Vidare är
$$ \overline{z}\cdot\overline{w}=(a-ib)(c-id)=ac-bd-i(ad+bc)$$
Alltså gäller (övning 1.47 b)
$$ \overline{zw}=\overline{z}\cdot\overline{w}$$
Av detta följer vidare
$$ |zw|^2=(zw)\cdot \overline{zw}=z\cdot w\cdot\overline{z}\cdot \overline{w}= (z\cdot\overline{z})\cdot (w\cdot\overline{w})=|z|^2\cdot |w|^2=(|z|\cdot |w|)^2$$
och drar vi kvadratroten ur båda ytterleden så får vi
$$ |zw|=|z|\cdot |w|$$
Däremot skall man komma ihåg att $|z+w|$ i allmänhet inte är lika
med $|z|+|w|$, utan bara att det gäller
$$ |z+w|\le |z|+|w|$$
vilket kallas triangelolikheten eftersom det kan tolkas som att längden av en sida i en triangel altid är mindre än summan av de övriga två. Beviset hoppar vi över.
Avsnitt 13.7
Lämpliga övningsuppgifter till Lektion 8
Välj bland följande uppgifter i boken: 1.44 - 1.47, 13.21 - 13.23

