Lösningar 18

Matematik för naturvetare 15hp

Hoppa till: navigering, sök

Lösningar till några övningar till lektion 18

Tillbaka till lösningarna



10.5.a)\int_0^{\infty}e^{-2x}\, dx=\lim_{T\to\infty}\int_0^Te^{-2x}\, dx=\lim_{T\to\infty}\left[-\frac{e^{-2x}}{2}\right]_0^T= \lim_{T\to\infty}\frac{1-e^{-2T}}{2}=\frac{1}{2}


b)Här måste vi dela upp integrationsintervallet: 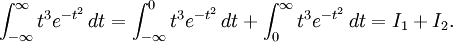\int_{-\infty}^{\infty}t^3e^{-t^2}\, dt=\int_{-\infty}^{0}t^3e^{-t^2}\, dt+\int_{0}^{\infty}t^3e^{-t^2}\, dt=I_1+I_2. Substitutionen $s=-t$ ger 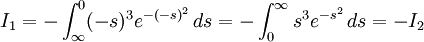I_1=-\int_{\infty}^0(-s)^3e^{-(-s)^2}\, ds=-\int_0^{\infty}s^3e^{-s^2}\, ds=-I_2 vilket visar att integralen är 0.


c)\begin{array}{lll} \int_{-\infty}^\pi{}e^x\sin 2x\, dx&=& \left[e^x\sin 2x\right]_{-\infty}^\pi{}-2\int_{-\infty}^\pi{}e^x\cos 2x\, dx\\ &=& -2\left[e^x\cos 2x\right]_{-\infty}^\pi{}-4\int_{-\infty}^\pi{}e^x\sin 2x\, dx\\ &=& -2e^\pi{}-4\int_{-\infty}^\pi{}e^x\sin 2x\, dx\end{array} Alltså är <math> \int_{-\infty}^\pi{}e^x\sin 2x\, dx=-\frac{2e^\pi{}}{5}.


d.\int_0^1x\ln x\, dx=\left[\frac{x^2}{2}\, \ln x\right]_0^1-\int_0^1\frac{x^2}{2}\cdot\frac{1}{x}\, dx= -\int_0^1\frac{x}{2}\, dx=-\left[\frac{x^2}{4}\right]_0^1=-\frac{1}{4}


e)\int_1^3\frac{1}{\sqrt{x-1}}\, dx=\left[2\sqrt{x-1}\right]_1^3=2\sqrt 2


f)\int_1^{\infty}\frac{1}{(x+1)^3}\, dx=\left[-\frac{1}{2(x+1)^2}\right]_1^{\infty}=\frac{1}{8}


10.6.d)Till att börja med är \begin{array}{lll} \int_0^T\left(\frac{x}{2x^2+1}-\frac{1}{1+2x}\right)\, dx&=&\left[\frac{1}{4}\ln(2x^2+1)-\frac{1}{2}\ln(1+2x)\right]_0^T\\ &=& \frac{1}{4}\ln\frac{2T^2+1}{(1+2T)^2}=\frac{1}{4}\ln\frac{2+1/T^2}{(2+1/T)^2}.\end{array} När $T\to\infty$ så går detta mot <math> \frac{1}{4}\ln\frac{2}{2^2}=-\frac{1}{4}\ln 2, som alltså är den generaliserade integralens värde.


10.14)Kvadratkomplettering ger 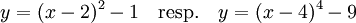y=(x-2)^2-1\quad\mbox{resp.}\quad y=(x-4)^4-9 och med hjälp av detta kan man lätta skissa graferna:

\begin{figure}[htbp] 

  \centering
  \includegraphics[width=7cm]{Fig1dag18.jpg}
  %\caption{A Saddle}

\end{figure}

Grafen till $y=x^2-4x+3$ skär $x$-axeln i 1 och 3 medan grafen till $y=x^2-8x+7$ skär axeln i 1 och 7. Den sökta arean är således 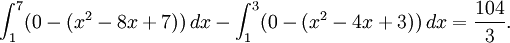\int_1^7(0-(x^2-8x+7))\, dx-\int_1^3(0-(x^2-4x+3))\, dx=\frac{104}{3}.


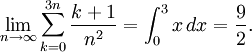
10.18)Omskrivningen \sum_{k=0}^{3n}\frac{k+1}{n^2}= \sum_{k=1}^{3n+1}\frac{1}{n}\cdot\frac{k}{n}=\sum_{k=1}^{3n}\frac{1}{n}\cdot\frac{k}{n}+ \frac{3n+1}{n^2} visar att summan är en Riemannsumma för $f(x)=x$ från $x=0$ till $x=3$ plus en term $(3n+1)/n^2$. Den extra termen går mot 0 då $n\to\infty$, så gränsvärdet är \lim_{n\to\infty}\sum_{k=0}^{3n}\frac{k+1}{n^2}=\int_0^3x\, dx=\frac{9}{2}.


10.19)Om man skriver 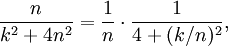\frac{n}{k^2+4n^2}=\frac{1}{n}\cdot\frac{1}{4+(k/n)^2}, så ser man att summan är en Riemannsumma för $f(x)=1/(4+x^2)$ från $x=0$ till $x=2$, varför gränsvärdet är \int_0^2\frac{dx}{4+x^2}=\frac{1}{4}\int_0^2\frac{dx}{1+(x/2)^2}=\frac{1}{4}\left[2\arctan\frac{x}{2}\right]_0^2=\frac{\pi{}}{8}.


10.20)Tangentens lutning är $k=3(-2)^2+6(-2)-4=-4$, så dess ekvation är 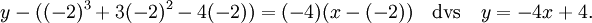y-((-2)^3+3(-2)^2-4(-2))=(-4)(x-(-2))\quad\mbox{dvs}\quad y=-4x+4. Vi måste hitta skärningspunkterna mellan tangenten och kurvan, dvs lösningarna till ekvationen $x^3+3x^2-4x=-4x+4$. Hyfsning ger $x^3+3x^2-4=0$. Nu är det ju faktiskt så att vi vet en rot, nämligen $x=-2$ och faktorisering ger $(x+2)(x^2+x-2)=0$. Rötterna till andragradspolynomet är 1 och $-2$, så skärningspunkterna är $x=-2$ och $x=1$. (Det är inte en slump att $-2$ är en dubbelrot, utan det beror på att linjen $y=-4x+4$ är tangent till kurvan. Detta behöver vi dock inte bekymra oss om här.) Frågan är nu om kurvan ligger över eller under tangenten mellan $-2$ och 1. Eftersom $0^3+3\cdot 0^2-4\cdot 0=0$ och $-4\cdot 0+4=4$, så ligger tangenten över kurvan. 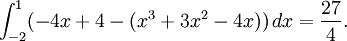Den sökta arean är \int_{-2}^1(-4x+4-(x^3+3x^2-4x))\, dx=\frac{27}{4}.


12.1. a.V=\pi{}\int_0^2(2x-x^2)^2\, dx=\pi{}\int_0^2(x^4-4x^3+4x^2)\, dx=\pi{}\left[\frac{x^5}{5}-x^4+\frac{4x^3}{3}\right]_0^2=\frac{16\pi{}}{15}


b)V=\pi{}\int_0^1(e^x)^2\, dx=\pi{}\int_0^1e^{2x}\, dx=\pi{}\left[\frac{e^{2x}}{2}\right]_0^1=\frac{\pi{}(e^2-1)}{2}


c)V=\pi{}\int_0^\pi{}\sin^2\, dx=\pi{}\int_0^\pi{}\frac{1-\cos 2x}{2}\, dx=\pi{}\left[\frac{x}{2}-\frac{\sin 2x}{4}\right]_0^\pi{}= \frac{\pi{}^2}{2}


d)\begin{array}{lll} V&=&\pi{}\int_1^e(\ln x)^2\, dx=\left\{\begin{array}{ccccc} x&=&e^t\\ dx&=&e^t\, dt\end{array}\right\}=\pi{}\int_0^1t^2e^t\, dt\\ &=& \pi{}\left[t^2e^t\right]_0^1-2\pi{}\int_0^1te^t\, dt=\pi{}e-2\pi{}\left[te^t\right]_0^1+2\pi{}\int_0^1e^t\, dt\\ &=& \pi{}e-2\pi{}e+2\pi{}\left[e^t\right]_0^1=\pi{}(e-2)\end{array} '''12.2)'''Grafen skär $y$-axeln för $x=0$, vilket ger $y=5$. Radien i en skiva på höjden $y$ är $x=5/y-1$ och dess area är $\pi{}y^2=\pi{}(5/y-1)^2$. Volymen av en skiva med tjocklek $dy$ är alltså $\pi{}y^2\, dy=\pi{}(5/y-1)^2\, dy$ så volymen av kroppen är <math>\begin{array}{lll} V&=&\pi{}\int_2^5\left(\frac{5}{y}-1\right)^2\, dy=\pi{}\int_2^5\left(\frac{25}{y^2}-\frac{10}{y}+1\right)\, dy\\ &=& \pi{}\left[-\frac{25}{y}-10\ln |y|+y\right]_2^5 =\pi{}\left(\frac{21}{2}-10\ln\frac{5}{2}\right).\end{array} '''12.4)'''<math> V=\pi{}\int_{-\infty}^0(e^y)^2\, dy=\pi{}\int_{-\infty}^0e^{2y}\, dy=\pi{}\left[\frac{e^{2y}}{2}\right]_{-\infty}^0=\frac{\pi{}}{2}


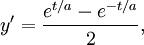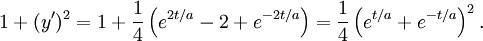12.7)Till att börja med har vi y'=\frac{e^{t/a}-e^{-t/a}}{2}, så 1+(y')^2=1+\frac{1}{4}\left(e^{2t/a}-2+e^{-2t/a}\right)=\frac{1}{4}\left(e^{t/a}+e^{-t/a}\right)^2. Kurvans längd är således L=\int_0^a\sqrt{1+(y')^2}\, dt=\frac{1}{2}\int_0^a(e^{t/a}+e^{-t/a})\, dt= \frac{a}{2}\left[e^{t/a}-e^{-t/a}\right]_0^a=\frac{a(e-e^{-1})}{2}.


12.13)Antalet dödsfall är ungefär \begin{array}{lll} \int_0^{30}V_d(t)\, dt&=&3560\int_0^{30}\frac{dt}{(e^{0,2t-3,4}+e^{-(0,2t-3,4)})^2}= \left\{\begin{array}{ccc} z&=&e^{0,2t-3,4}\\ t&=&5(3,4+\ln z)\\ dt&=&5dz/z\end{array}\right\}\\ &=& 3560\cdot 5\int_{e^{-3,4}}^{e^{2,6}}\frac{dz/z}{(z+z^{-1})}= 3560\cdot 5\int_{e^{-3,4}}^{e^{2,6}}\frac{z\, dz}{(1+z^2)^2}\\ &=&3560\cdot 5\left[-\frac{1}{1+z^2}\right]_{e^{-3,4}}^{e^{2,6}}\approx 8800.\end{array} '''12.15)'''Mer allmänt betraktar vi $N$ bin som samlas tätt i ett klot med radie $R$. Klotets volym är $V=4\pi{}R^3/3$. Ett tunt sfäriskt skal med radie $r$ och tjocklek $dr$ har volym $4\pi{}r^2\, dr$ (eftersom arean är $4\pi{}r^2$), så antalet bin i skalet är <math> \frac{4\pi{}r^2\ dr}{4\pi{}R^3/3}\cdot N och deras sammanlagda avstånd till medelpunkten får vi genom att multiplicera med $r$. Det blir 3N\left(\frac{r}{R}\right)^3dr. Binas medelavstånd blir \frac{1}{N}\cdot 3N\int_0^R\left(\frac{r}{R}\right)^3dr=\frac{3}{R^3}\left[\frac{r^4}{4}\right]_0^R= \frac{3R}{4}.

Den här artikeln är hämtad från http://wiki.math.se/wikis/mm1001_0701/index.php/L%C3%B6sningar_18
Personliga verktyg