Lektion 7

Matematik för naturvetare 15hp

Hoppa till: navigering, sök

Välkommen till Lektion 7!

I den här lektionen ska vi studera de användbara trigonometriska funkionerna och dess egenskaper.

Du ska studera följande kapitel i boken:

  • 4.5 Trigonometriska funktioner
  • 4.6 Trigonometriska formler
  • 4.7 Arcusfunktioner


Viktiga saker att tänka på när du läser

Det finns en enorm mängd trigonometriska formler och samband och man skall naturligtvis inte försöka lära sig dem utantill. Det är klart att man vid behov kan slå upp dem i sin formelsamling, men ännu bättre är att lära sig en av formlerna och kunna härleda de övriga när man har behov av dem. Praktiskt taget alla formler kan härledas ur en enda, nämligen

cos(u − v) = cosucosv + sinusinv.

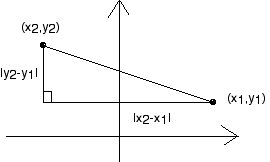
För att göra framställningen något sånär fullständig följer här ett bevis, som du kan läsa om du vill, men det ingår (som vanligt) inte i kursen. Vi behöver till att börja med den s k avståndsformeln i planet, som inte är något annat än Pythagoras sats: avståndet mellan punkterna $(x_{1},y_{1})$ och $(x_{2},y_{2})$ är

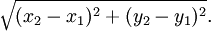
\sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2}.

Bevis: Kateterna i den rätvinkliga triangeln är $|x_{2}-x_{1}|$ och $|y_{2}-y_{1}|$ (lägg märke till absolutbeloppstecknen!), så Pythagoras sats ger att hypotenusans längd är

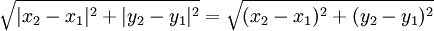
\sqrt{|x_{2}-x_{1}|^{2} + |y_{2}-y_{1}|^{2}} = \sqrt{(x_{2}-x_{1})^{2} + (y_{2}-y_{1})^{2}}

att beloppstecknen försvinner beror på att $(±a)^2=a^2$.


Bild:Fig1dag10.jpg


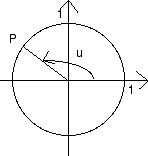
Vi repeterar definitionen av de trigonometriska funktionerna sinus och cosinus: Låt $u$ vara en vinkel och placera den med spetsen i origo och ett ben längs positiva $x$-axeln och så att det andra benet nås genom att man går i positiv led (det matematiska sättet att säga moturs eller motsols). Det andra vinkel benet skär enhetscirkeln (dvs den cirkel som har sin medelpunkt i origo $(0,0)$ och radie 1.) i en punkt $P$ och talen $\cos u, \quad \sin u$ definieras som $P$:s koordinater, dvs P = (cosu,sinu).


Bild: Fig2dag10.jpg


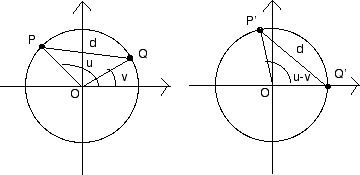
Låt nu $u$ och $v$ vara två vinklar och 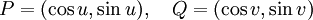P=(\cos u,\sin u), \quad Q=(\cos v,\sin v) motsvarande punkter på enhetscirkeln (se den vänstra figuren nedan). Beteckna avståndet mellan dem med $d$; enligt avståndsformeln är


$d^2=(\cos u-\cos v)^2+(\sin u-\sin v)^2$

$\quad = \cos^2u-2\cos u\cos v+\cos^2v+\sin^2u-2\sin u\sin v+\sin^2v$

$\quad = 2-2(\cos u\cos v+\sin u\sin v)$


eftersom $\cos^2u+\sin^2u=\cos^2v+\sin^2v=1$.

Bild:Fig3dag10.jpg


I figuren till höger har vi vridit triangeln $\triangle OQP$ ($O$ är origo) så att $Q$ hamnar i $Q'=(1,0)$. Då är $\wedge Q'OP'=u-v$, så $P'$ har koordinaterna $(\cos (u-v),\sin (u-v))$. Vi får nu ett annat uttryck för avståndet $d$, nämligen som avståndet mellan $(1,0)$ och $(\cos (u-v),\sin (u-v))$, dvs


$ d^2 = (1-\cos (u-v))^2+(0-\sin (u-v))^2$

$\quad = 1-2\cos (u-v)+\cos^2(u-v)+\sin^2(u-v)$

$\quad = 2-2\cos(u-v).$


Om vi jämför de två uttrycken för $d^2$ så får vi den sökta formeln.


Från formeln

cos(u − v) = cosucosv + sinusinv.

kan man härleda alla andra trigonometriska formler. Om vi byter $v$ mot $-v$ så får vi

$ \cos(u+v)=\cos u\cos (-v)+\sin u\sin (-v)=\cos u\cos v-\sin u\sin v $

eftersom

$\cos (-v)=\cos v, \quad \sin (-v)=-\sin v.$

Vi får vidare :


$ \sin(u+v) = \cos(\pi/2-(u+v))=\cos((\pi/2-u)-v)$

$\quad \quad = \cos (\pi/2-u)\cos v+\sin(\pi/2-u)\sin v = \sin u\cos v+\cos u\sin v $


och på samma sätt

$\sin(u-v)=\sin u\cos v-\cos u\sin v$.


Om man i additionsformlerna sätter $u=v$ så får man formlerna för dubbla vinkeln:

cos2u = cos2u − sin2u respektive sin2u = 2sinucosu.

Om vi använder den trigonometriska ettan så kan vi också skriva

$\cos 2u=2\cos^2u-1=1-2\sin^2u.$

De här formlerna ger i sin tur

$\cos^2 u=\frac{1+\cos 2u}{2},\quad \sin^2 u=\frac{1-\cos 2u}{2},$

och sätter vi här $v=2u$ så får vi formlerna för halva vinkeln:

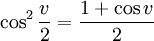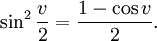
\cos^2\frac{v}{2}=\frac{1+\cos v}{2} samt \sin^2\frac{v}{2}=\frac{1-\cos v}{2}.

Man kan använda alla de här sambanden för att räkna ut fler exakta värden av sinus och cosinus. För vårt vidkommande är detta dock mindre viktigt, formlerna kommer vi mest att använda i samband med integration av trigonometriska funktioner.


Exempel 4.28 är lite bakvänt; för att visa formeln är det självklart lättast att börja med högerledet:


$ \cos (x-y)-\cos (x+y) = \cos x\cos y+\sin x\sin y-(\cos x\cos y-\sin x\sin y)$

$\quad \quad \quad = \cos x\cos y+\sin x\sin y-\cos x\cos y+\sin x\sin y$

$\quad \quad \quad = 2\sin x\sin y.$


De trigonometriska ekvationerna i Exempel 4.29 och 4.30. liksom i några av övningarna (4.28, 4.30) är väldigt artificiella och har som enda syfte att ge träning i att använda de trigonometriska funktionerna och sambanden.

Avsnitt 4.7 Ordet "arcus" är latin och betyder båge (jfr arc på engelska). Namnet arcusfunktioner kommer av att om $\sin x=a$, så Šr $x=\arcsin a$ längden av motsvarande båge på enhetscirkeln (enligt definitionen av radian och sinus). Ett annat namn är cyklometriska (cirkelmätning på grekiska) funktioner. De två viktigaste är arcsin och arctan. Kom ihåg att

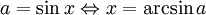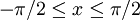
a=\sin x \Leftrightarrow x=\arcsin a\ och \ -\pi/2\le x\le \pi/2

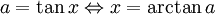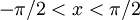
a=\tan x \Leftrightarrow x=\arctan a\ och \ -\pi/2< x< \pi/2

Observera också att man inte kan säga att man genom att skriva $x=\arcsin a$ har "löst" ekvationen $a=\sin x$; det enda man har gjort är att införa en beteckning för lösningen.


Studera Exempel 4.35 noga.


Lämpliga övningsuppgifter till Lektion 7

Välj bland följande uppgifter i boken: 4.17-4.18, 4.20, 4.22-4.28, 4.30, 4.31 samt 4.33-4.35.


Tillbaka till läsanvisningarna

Den här artikeln är hämtad från http://wiki.math.se/wikis/mm1001_0701/index.php/Lektion_7
Personliga verktyg