Lösningar 17
Matematik för naturvetare 15hp
Lösningar till några övningar till lektion 17
10.3.a)
![\begin{array}{lll} \int_{0}^{\pi}\sin\frac{x}{2}\, dx&=&\left\{\begin{array}{ccc} x/2&=&t\\ dx&=&2dt\end{array}\right\}=\int_{0}^{\pi{}/2}\sin t\, 2dt\\ &=& 2\left[-\cos t\right]_{0}^{\pi{}/2}=2(-\cos(\pi{}/2)-(-\cos 0))=2\end{array}](/wikis/mm1001_0701/images/math/f/5/3/f536d97c94db85a8611cb9ab47b6b48f.png)
b.
![\int_{0}^1\frac{2}{1+x^2}\, dx=\left[2\arctan x\right]_{0}^1=2(\arctan 1-\arctan 0)=\pi{}/2](/wikis/mm1001_0701/images/math/2/0/f/20f7f3faeed6bed13bb46077f954cb9e.png)
c. ![\int_{-1}^2(x-2x^3)\, dx=\left[x^2/2-x^4/2\right]_{-1}^2= 2^2/2-2^4/2-((-1)^2/2-(-1)^4)/2)=-6](/wikis/mm1001_0701/images/math/0/5/e/05e875e93de25b28a056ee7a9110444a.png)
d.
![\begin{array}{lll} \int_{-1}^{1/2}\sqrt{2-4x}\, dx&=&\left\{\begin{array}{ccc} 2-4x&=&t^2\\ dx&=&-t\, dt/2\end{array}\right\}\\ &=& \int_{\sqrt 6}^{0}(-t^2/2)\, dt=(1/2)\int_{0}^{\sqrt 6}t^2\, dt = (1/2)\left[\frac{t^3}{3}\right]_{0}^{\sqrt 6}=\sqrt 6\end{array}](/wikis/mm1001_0701/images/math/d/c/7/dc7724af3dd5f4bbccde5b02d28d2749.png)
e.
![\int_{3}^5\frac{7}{x-1}\, dx=\left[7\ln|x-1|\right]_{3}^5= 7(\ln 4-\ln 2)=7\ln\frac{4}{2}=7\ln 2](/wikis/mm1001_0701/images/math/d/8/1/d81e821fb9e0354ed20a01a4448e81dc.png)
f. ![\int_{0}^{-2}\frac{1}{(1-x)^2}\, dx=\left\{\begin{array}{cccc} 1-x&=&t\\ dx&=&-dt\end{array}\right\}=\int_{1}^{3}\frac{-1}{t^2}\, dt= \left[\frac{1}{t}\right]_{1}^3=-\frac{2}{3}](/wikis/mm1001_0701/images/math/e/2/f/e2f51b64b3711f7d1259efcfa08f5345.png)
10.4.a.
![\begin{array}{lll} \int_{\pi{}}^0\tan\frac{x}{4}\, dx&=&\int_{0}^\pi{}\frac{\sin(x/4)}{\cos(x/4)}\, dx= \left\{\begin{array}{ccc} \cos(x/4)&=&t\\ \sin(x/4)\, dx&=&-4\, dt\end{array}\right\}\\ &=& -4\int_{1/\sqrt 2}^{1}\frac{dt}{t}= -4\left[\ln|t|\right]_{1/\sqrt 2}^1= (-4)\left(\ln 1-\ln\frac{1}{\sqrt 2}\right)\\ &=&-2\,\ln 2\end{array}](/wikis/mm1001_0701/images/math/6/d/7/6d7e36b822ab0a703848ebfe7b994fa0.png)
b.
Enligt en formel för halva vinkeln är $\cos^2x=(1+\cos 2x)/2$, så
![\begin{array}{lll} \int_{0}^{\pi{}/6}\cos^2x\, dx&=&\frac{1}{2}\int_{0}^{\pi{}/6}(1+\cos 2x)\, dx= \frac{1}{2}\left[x+\frac{\sin 2x}{2}\right]_{0}^{\pi{}/6}\\ &=& \frac{1}{2}\left(\frac{\pi{}}{6}+\frac{\sqrt 3}{4}\right)= \frac{\pi{}}{12}+\frac{\sqrt 3}{8}\end{array}](/wikis/mm1001_0701/images/math/5/6/7/5675fa881b97b26de448074361cee2ea.png)
c.
![\begin{array}{lll} \int_{0}^1t^3(1-t^4)^2\, dt&=&\left\{\begin{array}{ccc} 1-t^4&=&x\\ t^3\, dt&=&-dx/4\end{array}\right\} = -\frac{1}{4}\int_{1}^{0}x^2\, dx\\ &=& \frac{1}{4}\left[\frac{x^3}{3}\right]_{0}^1= \frac{1}{12}\end{array}](/wikis/mm1001_0701/images/math/a/c/7/ac7415e7b4e69167ee64b2cb40600532.png)
d.
Partialintegrera och välj $(x^2-1)/2$ som primitiv funktion till $x$:
![\begin{array}{lll} \int_{0}^1x\ln(x+1)\, dx&=& \left[\frac{x^2-1}{2}\, \ln(x+1)\right]_{0}^1-\int_{0}^1\frac{x^2-1}{2(x+1)}\, dx\\ &=& -\frac{1}{2}\int_{0}^1(x-1)\, dx=-\frac{1}{2}\left[\frac{x^2}{2}-x\right]_{0}^1 =\frac{1}{4}\end{array}](/wikis/mm1001_0701/images/math/f/1/7/f17a9d74cf0af6147fc7e6dc7121efd6.png)
e.
![\begin{array}{lll} \int_{1}^e\frac{\ln x}{x^3}\, dx&=& \left[-\frac{\ln x}{2x^2}\right]_{1}^e+\frac{1}{2}\int_{1}^e\frac{dx}{x^3}\\ &=& -\frac{1}{2e^2}+\frac{1}{2}\left[-\frac{1}{2x^2}\right]_{1}^e= \frac{1}{4}\left(1-\frac{3}{e^2}\right)\end{array}](/wikis/mm1001_0701/images/math/1/8/3/183e748b84c461dee0f2d652e8afc081.png)
f.
![\begin{array}{lll} \int_{1}^{14}(2x-1)^{1/3}\, dx &=& \left\{\begin{array}{ccc} 2x-1&=&t\\ dx&=&dt/2\end{array}\right\}= \frac{1}{2}\int_{1}^{27}t^{1/3}\, dt\\ &=& \frac{1}{2}\left[\frac{t^{4/3}}{4/3}\right]_{1}^{27}= \frac{3}{8}\left(27^{4/3}-1^{4/3}\right)\\ &=& \frac{3}{8}((3^3)^{4/3}-1)= \frac{3}{8}(3^4-1)=30\end{array}](/wikis/mm1001_0701/images/math/4/6/4/464da4c86d758483774e4f3343bfcd8a.png)
10.6.a)
![\int_{0}^1(x^2-2)^2\, dx=\int_{0}^1(x^4-4x^2+4)\, dx=\left[\frac{x^5}{5}-\frac{4x^3}{3}+4x\right]_{0}^1= \frac{1}{5}-\frac{4}{3}+4=\frac{43}{15}](/wikis/mm1001_0701/images/math/8/f/2/8f2f13dc0e9bc730220b99ed11821686.png)
b.
Integralen är 0 eftersom undre och övre gränsen är lika.
c.
![\begin{array}{lll} \int_{\pi{}/4}^{\pi{}/2}\sin^3r\, dr&=& \int_{\pi{}/4}^{\pi{}/2}(1-\cos^2r)\sin r\, dr=\left\{\begin{array}{ccc} \cos r&=&x\\ \sin r\, dr&=&-dx\end{array}\right\}\\ &=& -\int_{1/\sqrt 2}^0(1-x^2)\, dx=\left[x-\frac{x^3}{3}\right]_{0}^{1\sqrt 2} = \frac{1}{\sqrt 2}-\frac{1}{6\sqrt 2}=\frac{5}{6\sqrt 2}\end{array}](/wikis/mm1001_0701/images/math/d/3/0/d306b1a763e050438116185377ac918c.png)
f.
![\begin{array}{lll} \int_{0}^{\pi{}/4}\tan x\, dx&=&\int_{0}^{\pi{}/4}\frac{\sin x}{\cos x}\, dx= \left\{\begin{array}{ccc} \cos x&=&t\\ \sin x\, dx&=& -\, dt\end{array}\right\}\\ &=& -\int_{1}^{1/\sqrt 2}\frac{dt}{t}=\left[\ln|t|\right]_{1}^{1/\sqrt 2}=-\ln\frac{1}{\sqrt 2}=\frac{\ln 2}{2}\end{array}](/wikis/mm1001_0701/images/math/b/5/e/b5ee1b1a6cb484746784b56772ee4b3f.png)
g.
Här måste man komma ihåg att $1/\cos^2t$ är derivatan av $\tan t$, så att
![\int_{0}^{\pi{}/6}\frac{dt}{\cos^2t}=\left[\tan x\right]_{0}^{\pi{}/6}=\tan\frac{\pi{}}{6}=\frac{1/2}{\sqrt 3/2}=\frac{1}{\sqrt 3}](/wikis/mm1001_0701/images/math/3/2/c/32cef7198e63f764f1e585a6dfd40a1c.png)
h.
![\begin{array}{lll} \int_{0}^{\pi{}/4}\frac{\sin x}{1+\tan^2x}\, dx&=& \int_{0}^{\pi{}/4}\frac{\sin x\cos^2x}{\cos^2x+\sin^2x}\, dx= \int_{0}^{\pi{}/4}\sin x\cos^2x\, dx\\ &=& \left\{\begin{array}{ccc} \cos x&=&t\\ \sin x\, dx&=& -t\end{array}\right\}= -\int_{1}^{1/\sqrt 2}t^2\, dt\\ &=& \left[\frac{t^3}{3}\right]_{1/\sqrt 2}^1=\frac{1}{3}\left(1-\frac{1}{2\sqrt 2}\right)\end{array}](/wikis/mm1001_0701/images/math/3/3/5/335b8e9f11e6e911a3ec2f9dd2949b3c.png)
10.7.a)
![\begin{array}{lll} \int_{-3}^{-2}t^2\sqrt{t+3}\, dt&=& \left\{\begin{array}{ccc} t+3&=&x^2\\ dt&=&2x\, dx\end{array}\right\}= \int_{0}^{1}(x^2-3)^2\cdot x\cdot 2x\, dx\\ &=& 2\int_{0}^{1}(x^6-6x^4+9x^2)\, dx= 2\left[\frac{x^7}{7}-\frac{6x^5}{5}+3x^3\right]_{0}^1\\ &=& 2\left(\frac{1}{7}-\frac{6}{5}+3\right)=\frac{136}{35}=3\frac{31}{35} \end{array}](/wikis/mm1001_0701/images/math/3/f/d/3fd9686e0148de4343f3ab3f7a8e9183.png)
b.
![\begin{array}{lll} \int_{0}^1\frac{\ln(3x+1)}{3x+1}\, dx&=&\left\{\begin{array}{ccc} \ln(3x+1)&=&t\\ dx/(3x+1) &=& dt/3\end{array}\right\}= \frac{1}{3}\int_{0}^{\ln 4}t\, dt\\ &=&\frac{1}{3}\left[\frac{t^2}{2}\right]_{0}^{\ln 4}=\frac{1}{6}\,(\ln 4)^2= \frac{2}{3}\,(\ln 2)^2 \end{array}](/wikis/mm1001_0701/images/math/7/8/d/78d5919eeea380bf92ec6c147fbfd93a.png)
c.
![\begin{array}{lll} \int_{0}^{1/4}\frac{dx}{\sqrt{1-4x^2}}&=&\left\{\begin{array}{ccc} 2x&=&t\\ dx&=&dt/2\end{array}\right\}= \frac{1}{2}\int_{0}^{1/2}\frac{dt}{\sqrt{1-t^2}}\\ &=& \frac{1}{2}\left[\arcsin t\right]_{0}^{1/2}=\frac{1}{2}\arcsin\frac{1}{2}= \frac{\pi{}}{12}\end{array}](/wikis/mm1001_0701/images/math/1/e/7/1e7ea20ac9bbbef44571ae6b777dc6fc.png)
d.
Här måste man först undersöka vad $x^2-x-2$ har för tecken i olika intervall. Man kan nämligen inte s a s integrera under absolutbeloppet, det fungerar inte på samma sätt som en parentes. Nu har vi $x^2-x-2=(x-2)(x+1)$ med teckenschemat
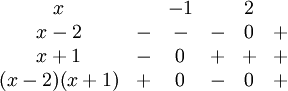
Alltså är $|x^2-x-2|=x^2-x-2$ då $x\le -1$ och då $x\ge 2$ och
$|x^2-x-2|=-(x^2-x-2)$ då $-1\le x\le 2$. Detta ger
![\begin{array}{lll} \int_{-2}^3|x^2-x-2|\, dx&=& \int_{-2}^{-1}(x^2-x-2)\, dx-\int_{-1}^2(x^2-x-2)\, dx\\ &+& \int_{2}^{3}(x^2-x-2)\, dx\\ &=& \left[\frac{x^3}{3}-\frac{x^2}{2}-2x\right]_{-2}^{-1}- \left[\frac{x^3}{3}-\frac{x^2}{2}-2x\right]_{-1}^{2}\\ &+& \left[\frac{x^3}{3}-\frac{x^2}{2}-2x\right]_{2}^{3} =\frac{49}{6}\end{array}](/wikis/mm1001_0701/images/math/d/4/e/d4efe1f6645c4b6caa12a2f698d8237d.png)
e.
![\begin{array}{lll} \int_{0}^2\frac{dx}{x^2+2x+2}&=&\int_{0}^2\frac{dx}{1+(x+1)^2}= \left[\arctan(x+1)\right]_{0}^2=\arctan 3-\frac{\pi{}}{4}\end{array}](/wikis/mm1001_0701/images/math/d/b/4/db46ddb0c1ff6015a88c713ab1797f59.png)
f.
![\begin{array}{lll} \int_{0}^1\arctan x\, dx&=&\left[x\arctan x\right]_{0}^1- \int_{0}^1\frac{x}{1+x^2}\, dx\\ &=& \arctan 1-\frac{1}{2}\int_{0}^1\frac{2x}{1+x^2}\, dx= \frac{\pi{}}{4}-\frac{1}{2}\left[\ln |1+x^2|\right]_{0}^1\\ &=& \frac{\pi{}}{4}-\frac{1}{2}\ln 2\end{array}](/wikis/mm1001_0701/images/math/5/b/7/5b73528ac0d49d9414dd51b81ed26c58.png)
10.8.
Vi har ju (enligt huvudsatsen)
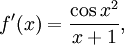
så
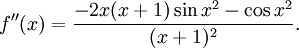
Alltså är $f(0)=-\cos 0=-1$.
10.9.
Derivatan är $f'(x)=(x^2-1)e^x=(x+1)(x-1)e^x$ med nollställen $±1$. Teckenschemat är
Misslyckades med att tolka formel. (okänt fel): \begin{array}{cccccc} x & & -1 & & 1 &\\ \hline x+1 & - & 0 & + & + & + \\ x-1 & - & - & - & 0 & + \\ f' & + & 0 & - & 0 & +\end{array}
(lägg märke till att faktorn $e^x$ inte påverkar tecknet). Alltså är $-1$ ett lokalt maximum och 1 ett lokalt minimum. Värdena är $f(1)=0$ och
![\begin{array}{lll} f(-1)&=&\int_{1}^{-1}(t^2-1)e^t\, dt=\left[(t^2-1)e^t\right]_{1}^{-1}- 2\int_{1}^{-1}te^t\, dt\\ &=& 2\int_{-1}^1te^t\, dt=2\left[te^t\right]_{-1}^1-2\int e^t\, dt\\ &=& 2(e+e^{-1})-2\left[e^t\right]_{-1}^1=4e^{-1}\end{array}](/wikis/mm1001_0701/images/math/a/5/b/a5bb5a68dac9acce0a4b600254de9f3b.png)
10.10.
Gör substitutionen $x/a=t$, $dx=a\, dt$. Integralen blir
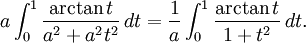
Gör substitutionen $z=\arctan t$, $dz=dt/(1+t^2)$. Då får vi
![\int_{0}^1\frac{\arctan t}{1+t^2}\, dt=\int_{0}^{\pi{}/4}z\, dz=\left[\frac{z^2}{2}\right]_{0}^{\pi{}/4}= \frac{\pi{}^2}{32}.](/wikis/mm1001_0701/images/math/6/1/4/6143334c8b9419120f6abb043d21059c.png)
Svaret är alltså att $a=\pi{}^2/32$.
10.12.a)
Arean är
![\int_{1}^2x^2\, dx=\left[\frac{x^3}{3}\right]_{1}^2=\frac{7}{3}.](/wikis/mm1001_0701/images/math/c/f/b/cfb9f0a7314db9875408741e99a4f871.png)
b.
Arean är
![\int_{1}^2\ln x\, dx=\left[x\ln x\right]_{1}^2-\int_{1}^2x\cdot\frac{1}{x}\, dx= 2\ln 2-\int_{1}^2\, dx=2\ln 2-1.](/wikis/mm1001_0701/images/math/5/4/c/54c16f7a643ea7512f3569bf973df6af.png)
c.
Kurvan $y=e^x$ skär linjen $y=2$ för $x=\ln 2$. Arean är således
![\int_{0}^{\ln 2}(2-e^x)\, dx=\left[2x-e^x\right]_{0}^{\ln 2}= 2\ln 2-2+1=2\ln 2-1.](/wikis/mm1001_0701/images/math/d/f/3/df31853f39d43cb384a66b14312484f2.png)
d.
Kurvan $y=x^2-2x-3$ skär $x$-axeln för $x=1±\sqrt{1+3}=1±2$, alltså för $x=-1$ och $x=3$. Arean är
![\int_{-1}^3(0-(x^2-2x-3))\, dx=-\left[\frac{x^3}{3}-x^2-3x\right]_{-1}^3=\frac{32}{3}.](/wikis/mm1001_0701/images/math/4/7/4/4746714f6ab046befb09338c12486c9e.png)

