Lektion 8
Matematik för naturvetare 15hp
Välkommen till Lektion 8!
Tillbaka till läsanvisningarna
I den här lektionen ska vi lära oss vad komplexa tal är för något och hur man räknar med dem och olika sätt att representera dem.
Du ska studera följande kapitel i boken:
- 1.9 De komplexa talen
- 13.7 Lite mer om komplexa tal
Viktiga saker att tänka på när du läser
Avsnitt 1.9
Lägg märke till att om $z=a+ib$, så är det talet $b$ som är
imaginärdelen, alltså inte $ib$. Både real- och imaginärdelarna av
$z$ är reella tal. Observera också att absolutbeloppet är
$|z|=\sqrt{a^2+b^2}$, inte $\sqrt{a^2+(ib)^2}$. Om $b=0$ så är $z=a$
ett reellt tal med absolutbelopp $|z|=\sqrt{a^2}=|a|$, där det sista
ledet är det vanliga reella absolutbeloppet. För reella tal
överensstämmer således det komplexa absolutbeloppet med det reella.
Med hjälp av Pythagoras sats så ser vi att $|a+ib|=\sqrt{a^2+b^2}$ är avståndet från origo till punkten $a+ib$ (se längst ned på sid 49).
Addition, subtraktion och multiplikation av komplexa tal går till så att man "räknar som vanligt" men kommer ihåg att $i^2=-1$. Det betyder t.ex. att produkten av $a+ib$ och $c+id$ är
$$(a+ib)(c+id)=(ac-bd)+i(ad+bc)$$
Tillämpar man detta på produkten $z\cdot \overline z$ där $z=a+ib$ så får man $z\cdot \overline z=(a+ib)(a-ib)=a^2+b^2=|z|^2$ (se också här längst ned på sid 49).
I Exempel 1.31 drar man kvadratroten ur ett negativt tal $\sqrt{-16}=±4i$. Normalt brukar man dock reservera beteckningen $\sqrt a$ för reella tal $a\ge 0$, annars är det lätt hänt att beteckningarna leder en vilse:
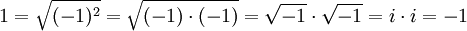
Var är felet?
Konjugering och absolutbelopp har vissa viktiga egenskaper som man ofta har användning av, men som inte diskuteras i avsnittet (se dock övning 1.47). Vi skall göra det här istället. Låt $z=a+ib$ vara ett komplext tal; dess konjugat är $\overline{z}=a-ib$, så
$$ z\cdot\overline{z}=(a+ib)(a-ib)=a^2-(ib^2)=a^2+b^2=|z|^2$$
Låt $w=c+id$ vara ett annat komplext tal. Då är
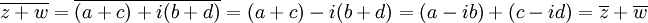
dvs konjugatet av en summa är lika med summan av konjugaten (se övning 1.47 a).
Motsvarande gäller för produkter:
$$ zw=(a+ib)(c+id)=ac-bd+i(ad+bc),\quad\mbox{så att}\quad \overline{zw}=ac-bd-i(ad+bc)$$
Vidare är
$$ \overline{z}\cdot\overline{w}=(a-ib)(c-id)=ac-bd-i(ad+bc)$$
Alltså gäller (övning 1.47 b)
$$ \overline{zw}=\overline{z}\cdot\overline{w}$$
Av detta följer vidare
$$ |zw|^2=(zw)\cdot \overline{zw}=z\cdot w\cdot\overline{z}\cdot \overline{w}= (z\cdot\overline{z})\cdot (w\cdot\overline{w})=|z|^2\cdot |w|^2=(|z|\cdot |w|)^2$$
och drar vi kvadratroten ur båda ytterleden så får vi
$$ |zw|=|z|\cdot |w|$$
Däremot skall man komma ihåg att $|z+w|$ i allmänhet inte är lika
med $|z|+|w|$, utan bara att det gäller
$$ |z+w|\le |z|+|w|$$
vilket kallas triangelolikheten eftersom det kan tolkas som att längden av en sida i en triangel altid är mindre än summan av de övriga två. Beviset hoppar vi över.
Avsnitt 13.7
I detta avsnitt får man lära sig att skriva ett komplext tal $z$ på "polär form", dvs man anger avståndet från $z$ till origo, $|z|$, och vilken vinkel, "argumentet", som linjen från origo till $z$ bildar med positiva reella axeln. Se också sid 121 för definition av denna vinkel. Flera olika vinklar beskriver samma läge för $z$. Man kan t.ex. använda vinklarna $90^\circ, -270^\circ, 450^\circ$ för att ge argumentet för ett komplext tal på den positiva imaginära axeln. Argumentet för $z$, som skrives $\arg z$ är alltså inte entydigt bestämt. Man kan alltid lägga till eller dra bort ett helt antal varv (dvs en multipel av $360^\circ$, eller $2\pi$ radianer). Som det står nederst på sid 353, så brukar man vanligen bestämma sig för att ange argumentet i intervallet
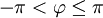
(observera att man skall ha sträng olikhet till vänster för att få entydighet).
Som det står ovanför bilden på sid 352, så är de polära koordinaterna för $z$ lika med $(|z|,\arg z)$. I rutan längst ned på samma sida står ett annat mer vanligt sätt att skriva den polära formen. Man måste dock komma ihåg att $\cos\varphi$ och $\sin\varphi$ inte får räknas ut. Talet $1+i$ har den polära formen som står på sid 353:
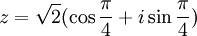
Skulle man stoppa in värdena på $\cos\frac{\pi}{4}=1/\sqrt2$ och $\sin\frac{\pi}{4}=1/\sqrt2$ så skulle man få $z=1+i$ vilket ju är den vanliga formen med rätvinkliga koordinater och inte den polära formen.
Av Sats 13.2 följer
Lämpliga övningsuppgifter till Lektion 8
Välj bland följande uppgifter i boken: 1.44 - 1.47, 13.21 - 13.23

