3.2 Rotekvationer
Sommarmatte 1
| Versionen från 26 april 2007 kl. 11.11 (redigera) Lina (Diskussion | bidrag) (→Teori) ← Gå till föregående ändring |
Versionen från 6 maj 2007 kl. 17.35 (redigera) (ogör) Tek (Diskussion | bidrag) (En del ändringar) Gå till nästa ändring → |
||
| Rad 1: | Rad 1: | ||
| + | __NOTOC__ | ||
| <table><tr><td width="600"> | <table><tr><td width="600"> | ||
| - | |||
| - | =3.2 Rotekvationer= | ||
| <div class="inforuta"> | <div class="inforuta"> | ||
| '''Innehåll:''' | '''Innehåll:''' | ||
| - | *Rotekvationer av typen $ \sqrt{ax+b}= cx +d $ | + | *Rotekvationer av typen $\,\sqrt{ax+b}= cx +d $ |
| *Falska rötter | *Falska rötter | ||
| </div> | </div> | ||
| <div class="inforuta"> | <div class="inforuta"> | ||
| - | '''Läromål:''' | + | '''Lärandemål:''' |
| Efter detta avsnitt ska du ha lärt dig att: | Efter detta avsnitt ska du ha lärt dig att: | ||
| - | *Lösa enkla rotekvationer med kvadrering och veta att lösningarna måste prövas | + | *Lösa enkla rotekvationer med kvadrering och veta att lösningarna måste prövas. |
| </div> | </div> | ||
| Rad 30: | Rad 29: | ||
| Det finns många olika varianter av rotekvationer, t.ex. | Det finns många olika varianter av rotekvationer, t.ex. | ||
| - | $$\sqrt{x} + 3x = 2$$ | + | $$\sqrt{x} + 3x = 2\,,$$ |
| - | $$\sqrt{x - 1} - 2x = x^2$$ | + | $$\sqrt{x - 1} - 2x = x^2\,,$$ |
| - | $$\sqrt[\scriptstyle3]{x + 2} = x$$ | + | $$\sqrt[\scriptstyle3]{x + 2} = x\,\mbox{.}$$ |
| Rad 40: | Rad 39: | ||
| Strategin för att uppnå detta är att skriva ekvationen | Strategin för att uppnå detta är att skriva ekvationen | ||
| så att rottecknet blir ensamt kvar på ena sidan av likhetstecknet. | så att rottecknet blir ensamt kvar på ena sidan av likhetstecknet. | ||
| - | Sedan kvadrerar man ekvationen (om det handlar om en kvadratrot), så att rottecknet försvinner. | + | Sedan kvadrerar man båda led i ekvationen (om det handlar om en kvadratrot), så att rottecknet försvinner och löser sedan den nya, kvadrerade, ekvationen. |
| När man kvadrerar en ekvation måste man tänka på att de lösningar som man får | När man kvadrerar en ekvation måste man tänka på att de lösningar som man får | ||
| fram kanske inte är lösningar till den ursprungliga ekvationen. Detta beror på att eventuella | fram kanske inte är lösningar till den ursprungliga ekvationen. Detta beror på att eventuella | ||
| Rad 52: | Rad 51: | ||
| '''Exempel 1''' | '''Exempel 1''' | ||
| - | Minustecken försvinner vid kvadrering. Betrakta en enkel (trivial) ekvation: | + | Minustecken försvinner vid kvadrering. Betrakta en enkel (trivial) ekvation |
| - | $$x = 2,$$ | + | $$x = 2\mbox{.}$$ |
| Om vi kvadrerar båda led i denna ekvation får vi | Om vi kvadrerar båda led i denna ekvation får vi | ||
| - | $$x^2 = 4 $$ | + | $$x^2 = 4\mbox{.}$$ |
| - | Denna nya ekvation har två lösningar $x = 2$ eller $x = -2$. | + | Denna nya ekvation har två lösningar $\,x = 2\,$ eller $\,x = -2\,$. |
| - | Lösningen $x = 2$ uppfyller den ursprungliga ekvationen medan $x = -2$ är en lösning dom uppstod i den kvaderade ekvationen. | + | Lösningen $\,x = 2\,$ uppfyller den ursprungliga ekvationen medan $\,x = -2\,$ är en lösning som uppstod i den kvadrerade ekvationen. |
| </div> | </div> | ||
| Rad 69: | Rad 68: | ||
| '''Exempel 2''' | '''Exempel 2''' | ||
| - | Lös ekvationen:$2\sqrt{x - 1} = 1 - x$ | + | Lös ekvationen $\ 2\sqrt{x - 1} = 1 - x\,$. |
| - | + | <br> | |
| - | + | <br> | |
| - | '''Lösning:''' | + | Tvåan framför rottecknet är en faktor. Vi kan dividera vänster- och högerled med 2, |
| - | + | men vi kan också låta tvåan stå kvar. Om vi kvadrerar ekvationen | |
| - | Tvåan framför rottecknet är en faktor. Vi kan dividera vänster- och högerled med två, | + | |
| - | men vi kan också låta tvåan stå kvar. Den stör oss inte. Om vi kvadrerar ekvationen | + | |
| som den är får vi | som den är får vi | ||
| - | + | $$4(x - 1) = (1 - x)^2$$ | |
| - | $4(x - 1) = (1 - x)^2 $ | + | |
| - | + | ||
| och utvecklar vi kvadraten fås | och utvecklar vi kvadraten fås | ||
| - | + | $$4(x - 1)= 1 - 2x + x^2\,\mbox{.}$$ | |
| - | $4(x - 1)= 1 - 2x + x^2$ | + | |
| - | + | ||
| Detta är en andragradsekvation, som kan skrivas | Detta är en andragradsekvation, som kan skrivas | ||
| + | $$x^2 - 6x + 5 = 0\,\mbox{.}$$ | ||
| - | $x^2 - 6x + 5 = 0$ | + | Denna kan lösas med kvadratkomplettering eller med den allmänna lösningsformeln. |
| - | + | Lösningarna blir $\,x = 3 \pm 2\,$, dvs. $\,x = 1\,$ eller $\,x = 5\,$. | |
| - | Denna kan lösas med kvadratkomplettering eller allmänna lösningsformeln. | + | |
| - | Lösningarna blir: | + | |
| - | + | ||
| - | $x = 3 \pm 2, $ dvs $ x = 1 $ eller $ x = 5. $ | + | |
| - | + | ||
| - | + | ||
| - | Eftersom vi kvaderar ekvationen finns risk att detta introducerar falska rötter och därför behöver vi pröva om $x=1$ och $x=5$ också är lösningarna i den ursprungliga rotekvationen: | + | |
| - | + | ||
| - | + | ||
| - | '''Testa $x = 1 \;$''' | + | |
| - | + | ||
| - | $x = 1 \;$ | + | |
| - | + | ||
| - | medför | + | |
| - | + | ||
| - | $\mbox{VL} = 2\sqrt{1 - 1} = 0 \; $ | + | |
| - | + | ||
| - | och | + | |
| - | + | ||
| - | $\mbox{HL} = 1 - 1 = 0. $ | + | |
| - | + | ||
| - | + | ||
| - | '''$\mbox{VL} = \mbox{HL.}$ Ekvationen är uppfylld!''' | + | |
| - | + | ||
| - | + | ||
| - | '''Testa $x = 5 \;$''' | + | |
| - | + | ||
| - | $x = 5 \; $ medför | + | |
| - | + | ||
| - | $ \mbox{VL} = 2\sqrt{5 - 1} = 2\cdot2 = 4 \; $ | + | |
| - | + | ||
| - | och | + | |
| - | + | ||
| - | $ \mbox{HL} = 1 - 5 = -4.$ | + | |
| - | + | ||
| - | '''$\mbox{VL} \ne \mbox{HL.}$ Ekvationen är inte uppfylld!''' | ||
| + | Eftersom vi kvadrerar ekvationen finns risken att detta introducerar falska rötter och därför behöver vi pröva om $\,x=1\,$ och $\,x=5\,$ också är lösningarna till den ursprungliga rotekvationen: | ||
| - | '''Ekvationen har alltså bara en lösning, $x = 1 \; \mbox{.}$''' | + | * $x = 1\,$ medför att $\,\mbox{VL} = 2\sqrt{1 - 1} = 0\,$ och $\,\mbox{HL} = 1 - 1 = 0\,$. Alltså är $\,\mbox{VL} = \mbox{HL}\,$ och ekvationen är uppfylld! |
| + | * $x = 5\,$ medför att $\,\mbox{VL} = 2\sqrt{5 - 1} = 2\cdot2 = 4\,$ och $\,\mbox{HL} = 1 - 5 = -4\,$. Alltså är $\,\mbox{VL} \ne \mbox{HL}$ och ekvationen är ''inte'' uppfylld! | ||
| + | Ekvationen har därmed bara en lösning $\,x = 1 \,$. | ||
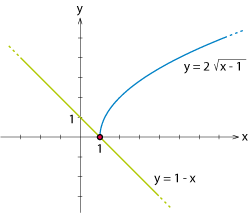
| - | De två funktionerna visas i kurvan nedan. | + | [[Bild:772637.gif||center]] |
| - | [[Bild:772637.gif]] | + | |
| </div> | </div> | ||
Versionen från 6 maj 2007 kl. 17.35
|
Innehåll:
Lärandemål: Efter detta avsnitt ska du ha lärt dig att:
|
|
TeoriDet finns många olika varianter av rotekvationer, t.ex. $$\sqrt{x} + 3x = 2\,,$$ $$\sqrt{x - 1} - 2x = x^2\,,$$ $$\sqrt[\scriptstyle3]{x + 2} = x\,\mbox{.}$$
Exempel 1 Minustecken försvinner vid kvadrering. Betrakta en enkel (trivial) ekvation $$x = 2\mbox{.}$$ Om vi kvadrerar båda led i denna ekvation får vi $$x^2 = 4\mbox{.}$$ Denna nya ekvation har två lösningar $\,x = 2\,$ eller $\,x = -2\,$. Lösningen $\,x = 2\,$ uppfyller den ursprungliga ekvationen medan $\,x = -2\,$ är en lösning som uppstod i den kvadrerade ekvationen. Exempel 2 Lös ekvationen $\ 2\sqrt{x - 1} = 1 - x\,$.
Denna kan lösas med kvadratkomplettering eller med den allmänna lösningsformeln. Lösningarna blir $\,x = 3 \pm 2\,$, dvs. $\,x = 1\,$ eller $\,x = 5\,$.
Ekvationen har därmed bara en lösning $\,x = 1 \,$. Råd för inläsning Tänk på att: När man kvadrerar en ekvation måste man tänka på att de lösningar som man får fram kanske inte är lösningar till den ursprungliga ekvationen, s. k. falska rötter. Detta beror på att eventuella minustecken försvinner. Man tappar information när man kvadrerar. Därför måste man verifiera att de lösningar man får fram, inte bara är lösningar till den kvadrerade ekvationen, utan också är lösningar till den ursprungliga ekvationen. Du ska alltid pröva lösningen i rotekvationer.
för dig som vill fördjupa dig ytterligare eller skulle vilja ha en längre förklaring Läs mer om Algebra i Theducations Gymnasielexikon Understanding Algebra - engelsk bok på nätet för högskoleförberedande studier
Vad är roten ur -- ? Webmath.com hjälper dig att förenkla rotuttryck
|
Repetition av rötter Rotekvationer är ekvationer där variabeln förekommer under ett rottecken. Det kan handla om både kvadratrötter, kubikrötter ellar andra rötter. Först något om beteckningar (se även avsnitt 1.4). Kvadratroten ur x betecknas: $ \sqrt{x} \; $ eller $ \; x^{1/2} $ och är beteckningen för det positiva tal (om x > 0) som kvadrerat blir x. Kubikroten ur x betecknas: $ \sqrt[\scriptstyle3]{x} \; $ eller $ \; x^{1/3}$ och är det tal som upphöjt i 3 blir x. Förväxla inte kubikroten med $3 \sqrt{x}$ som är tre gånger kvadratroten ur x. Kubikrötter kan dras ur negativa tal, och de kan vara negativa.
|