Sommarmatte 1
(Skillnad mellan versioner)
Versionen från 21 juni 2007 kl. 14.51
Övning 1.1:1
Beräkna (utan hjälp av räknedosa)
| a) |
$3-7-4+6-5$ |
b) |
$3-(7-4)+(6-5)$ |
| c) |
$3-(7-(4+6)-5)$ |
d) |
$3-(7-(4+6))-5$ |
|
| a) |
$-7$ |
b) |
$1$ |
| c) |
$11$ |
d) |
$1$ |
|
Övning 1.1:2
Beräkna (utan hjälp av räknedosa)
| a) |
$(3-(7-4))(6-5)$ |
b) |
$3-(((7-4)+6)-5)$ |
| c) |
$3\cdot(-7)-4\cdot(6-5)$ |
d) |
$3\cdot(-7)-(4+6)/(-5)$ |
|
| a) |
$0$ |
b) |
$-1$ |
| c) |
$-25$ |
d) |
$-19$ |
|
Övning 1.1:3
Vilka av följande tal tillhör de naturliga talen? heltalen?
rationella talen? irrationella talen? Förenkla först!
| a) |
$8$ |
b) |
$-4$ |
c) |
$8-4$ |
| d) |
$4-8$ |
e) |
$8(-4)$ |
f) |
$(-8)(-4)$ |
| g) |
$\displaystyle \frac{4}{-8}$ |
h) |
$\displaystyle \frac{-8}{-4}$ |
i) |
$\displaystyle \frac{\sqrt{2}}{3}$ |
| j) |
$\displaystyle \Bigl(\frac{4}{\sqrt{2}}\Bigr)^2$ |
k) |
$-\pi$ |
l) |
$\pi+1$ |
|
|
| a) |
naturliga talen, heltalen, rationella talen |
b) |
heltalen, rationella talen |
c) |
naturliga talen, heltalen, rationella talen |
| d) |
heltalen, rationella talen |
e) |
heltalen, rationella talen |
f) |
naturliga talen, heltalen, rationella talen |
| g) |
rationella talen |
h) |
naturliga talen, heltalen, rationella talen |
i) |
irrationella talen |
| j) |
naturliga talen, heltalen, rationella talen |
k) |
irrationella talen |
l) |
irrationella talen |
|
Övning 1.1:4
Ordna följande tal i storleksordning
| a) |
$\displaystyle 2,\ \frac{3}{5},\ \frac{5}{3}\ $ och $\ \displaystyle \frac{7}{3}$ |
| b) |
$\displaystyle -\frac{1}{2},\ -\frac{1}{5},\ -\frac{3}{10}\ $ och $\ \displaystyle -\frac{1}{3}$ |
| c) |
$\displaystyle \frac{1}{2},\ \frac{2}{3},\ \frac{3}{5},\ \frac{5}{8}\ $ och $\ \displaystyle \frac{21}{34}$ |
|
| a) |
$\displaystyle \frac{3}{5}<\frac{5}{3}<2<\frac{7}{3}$ |
| b) |
$\displaystyle -\frac{1}{2}<-\frac{1}{3}<-\frac{3}{10}<-\frac{1}{5}$ |
| c) |
$\displaystyle \frac{1}{2}<\frac{3}{5}<\frac{21}{34}<\frac{5}{8}<\frac{2}{3}$ |
|
Övning 1.1:5
Ange decimalutvecklingen med tre korrekta decimaler till
| a) |
$\displaystyle \frac{7}{6}$ |
b) |
$\displaystyle \frac{9}{4}$ |
c) |
$\displaystyle \frac{2}{7}$ |
d) |
$\sqrt{2}$ |
|
| a) |
$1{,}167$ |
b) |
$2{,}250$ |
c) |
$0{,}286$ |
d) |
$1{,}414$ |
|
Övning 1.1:6
Vilka av följande tal är rationella? Ange dem som en kvot mellan heltal.
| a) |
$3,14$ |
| b) |
$3{,}1416\,1416\,1416\,\dots$ |
| c) |
$0{,}2\,001\,001\,001\,\dots\,$ (därefter är var tredje decimal en 1:a och övriga 0) |
| d) |
$0{,}10\,100\,1000\,10000\,1\dots\, $ (en 1:a, en 0:a, en 1:a, två 0:or, en 1:a, tre 0:or osv.) |
|
| a) |
Talet är rationellt och lika med $\,314/100 = 157/50\,$. |
| b) |
Talet är rationellt och är lika med $\,31413/9999 = 10471/3333\,$. |
| c) |
Talet är rationellt och lika med $\,1999/9990\,$. |
| d) |
Talet är irrationellt. |
|
Övning 1.2:1
Skriv på gemensamt bråkstreck
| a) |
$\displaystyle \frac{7}{4}+\frac{11}{7}$ |
b) |
$\displaystyle \frac{2}{7}-\frac{1}{5}$ |
c) |
$\displaystyle \frac{1}{6}-\frac{2}{5}$ |
| d) |
$\displaystyle \frac{1}{3}+\frac{1}{4}+\frac{1}{5}$ |
e) |
$\displaystyle \frac{8}{7}+\frac{3}{4}-\frac{4}{3}$ |
|
| a) |
$\displaystyle \frac{93}{28}$ |
b) |
$\displaystyle \frac{3}{35}$ |
c) |
$\displaystyle -\frac{7}{30}$ |
| d) |
$\displaystyle \frac{47}{60}$ |
e) |
$\displaystyle \frac{47}{84}$ |
|
Övning 1.2:2
Bestäm minsta gemensamma nämnare
| a) |
$\displaystyle \frac{1}{6}+\frac{1}{10}$ |
b) |
$\displaystyle \frac{1}{4}-\frac{1}{8}$ |
| c) |
$\displaystyle \frac{1}{12}-\frac{1}{14}$ |
d) |
$\displaystyle \frac{2}{45}+\frac{1}{75}$ |
|
| a) |
$\displaystyle {30}$ |
b) |
$\displaystyle {8}$ |
| c) |
$\displaystyle {84}$ |
d) |
$\displaystyle {225}$ |
|
Övning 1.2:3
Beräkna följande uttryck genom att använda minsta gemensamma nämnare:
| a) |
$\displaystyle \frac{3}{20}+\frac{7}{50}-\frac{1}{10}$ |
b) |
$\displaystyle \frac{1}{24}+\frac{1}{40}-\frac{1}{16}$ |
|
|
| a) |
$\displaystyle \frac{19}{100}$ |
b) |
$\displaystyle \frac{1}{240}$ |
|
Övning 1.2:4
Förenkla följande uttryck genom att skriva på gemensamt bråkstreck. Bråket ska vara färdigförkortat.
| a) |
$\displaystyle\frac{\displaystyle\frac{3}{5}}{\displaystyle\frac{7}{10}}$ |
b) |
$\displaystyle\frac{\displaystyle\frac{2}{7}}{\displaystyle\frac{3}{8}}$ |
c) |
$\displaystyle\frac{\displaystyle\frac{1}{4}-\frac{1}{5}}{\displaystyle\frac{3}{10}}$ |
|
| a) |
$\displaystyle \frac{6}{7}$ |
b) |
$\displaystyle \frac{16}{21}$ |
c) |
$\displaystyle \frac{1}{6}$ |
|
Övning 1.2:5
Förenkla följande uttryck genom att skriva på gemensamt bråkstreck. Bråket ska vara färdigförkortat.
| a) |
$\displaystyle \frac{2}{\displaystyle \frac{1}{7}\displaystyle -\frac{1}{15}}$ |
b) |
$\displaystyle\frac{\displaystyle\frac{1}{2}\displaystyle+\frac{1}{3}}{\displaystyle\frac{1}{3}\displaystyle-\frac{1}{2}}$ |
c) |
$\displaystyle\frac{\displaystyle\frac{3}{10}\displaystyle-\frac{1}{5}}{\displaystyle\frac{7}{8}\displaystyle-\frac{3}{16}}$ |
|
|
| a) |
$\displaystyle \frac{105}{4}$ |
b) |
$-5$ |
c) |
$\displaystyle \frac{8}{55}$ |
|
Övning 1.2:6
Förenkla $\ \,\displaystyle \frac{\displaystyle \frac{2}{\displaystyle 3+\frac{1}{2}}\displaystyle + \frac{\displaystyle \frac{1}{2}}{\displaystyle \frac{1}{4}\displaystyle -\frac{1}{3}}}{\displaystyle \frac{1}{2}\displaystyle - \frac{3}{\displaystyle 2-\frac{2}{7}}}$
| $\displaystyle \frac{152}{35}$ |
Övning 1.3:1
Beräkna
| a) |
$2^3\cdot3^2$ |
b) |
$3^5\cdot9^{-2}$ |
c) |
$(-5)^3$ |
d) |
$\Bigl(\displaystyle \frac{2}{3}\Bigr)^{-3}$ |
|
| a) |
$72$ |
b) |
$3$ |
c) |
$-125$ |
d) |
$\displaystyle \frac{27}{8}$ |
|
Övning 1.3:2
Skriv som en potens av 2
| a) |
$2\cdot4\cdot8$ |
b) |
$0{,}25$ |
c) |
$1$ |
|
| a) |
$2^6$ |
b) |
$2^{-2}$ |
c) |
$2^0$ |
|
Övning 1.3:3
Skriv som en potens av 3
| a) |
$\displaystyle \frac{1}{3}$ |
b) |
$243$ |
c) |
$9^2$ |
d) |
$\displaystyle \frac{1}{27}$ |
e) |
$\displaystyle \frac{3}{9^2}$ |
|
| a) |
$3^{-1}$ |
b) |
$3^5$ |
c) |
$3^4$ |
d) |
$3^{-3}$ |
e) |
$3^{-3}$ |
|
Övning 1.3:4
Beräkna
| a) |
$2^{9}\cdot2^{-7}$ |
b) |
$3^{13}\cdot9^{-3}\cdot27^{\,-2}$ |
c) |
$\displaystyle \frac{5^{12}}{5^{-4}}\cdot(5^{2})^{-6}$ |
| d) |
$2^{2^{\scriptstyle3}}\cdot(-2)^{\scriptstyle-4}$ |
e) |
$625\cdot(5^{8}+5^{9})^{-1}$ |
|
| a) |
$4$ |
b) |
$3$ |
c) |
$625$ |
| d) |
$16$ |
e) |
$\displaystyle \frac{1}{3750}$ |
|
Övning 1.3:5
Beräkna
| a) |
$4^{1/2}$ |
b) |
$4^{-1/2}$ |
c) |
$9^{3/2}$ |
| d) |
$\left(47^{2/3} \right) ^{3}$ |
e) |
$3^{1{,}4}\cdot3^{0{,}6}$ |
f) |
$\bigl( 125 ^{1/3} \bigr)^2\cdot \bigl( 27^{1/3} \bigr)^{-2}\cdot9^{1/2}$ |
|
| a) |
$2$ |
b) |
$\displaystyle \frac{1}{2}$ |
c) |
$27$ |
| d) |
$2209$ |
e) |
$9$ |
f) |
$\displaystyle \frac{25}{3}$ |
|
Övning 1.3:6
Avgör vilket tal som är störst av
| a) |
$256^{1/3}\ $ och $\ 200^{1/3}$ |
b) |
$0{,}5^{-3}\ $ och $\ 0{,}4^{-3}$ |
c) |
$0{,}2^5\ $ och $\ 0{,}2^{7}$ |
| d) |
$400^{1/3}\ $ och $\ \bigl(5^{1/3}\bigr)^{4}$ |
e) |
$125^{1/2}\ $ och $\ 625^{1/3}$ |
f) |
$2^{56}\ $ och $\ 3^{40}$ |
|
| a) |
$256^{1/3}>200^{1/3}$ |
b) |
$0{,}4^{-3}>0{,}5^{-3}$ |
c) |
$0{,}2^{5}>0{,}2^{7}$ |
| d) |
$\bigl(5^{1/3}\bigr)^{4}>400^{1/3}$ |
e) |
$125^{1/2}>625^{1/3}$ |
f) |
$3^{40}>2^{56}$ |
|
Övning 2.1:1
Utveckla
| a) |
$3x(x-1)$ |
b) |
$(1+x-x^2)xy$ |
c) |
$-x^2(4-y^2)$ |
| d) |
$x^3y^2\left(\displaystyle \frac{1}{y} - \frac{1}{xy}+1\right)$ |
e) |
$(x-7)^2$ |
f) |
$(5+4y)^2$ |
| g) |
$(y^2-3x^3)^2$ |
h) |
$(5x^3+3x^5)^2$ |
|
| a) |
$3x^2-3x$ |
b) |
$xy+x^2y-x^3y$ |
c) |
$-4x^2+x^2y^2$ |
| d) |
$x^3y-x^2y+x^3y^2$ |
e) |
$x^2-14x+49$ |
f) |
$16y^2+40y+25$ |
| g) |
$9x^6-6x^3y^2+y^4$ |
h) |
$9x^{10}+30x^8+25x^6$ |
|
Övning 2.1:2
Utveckla och förenkla så långt som möjligt
| a) |
$(x-4)(x-5)-3x(2x-3)$ |
b) |
$(1-5x)(1+15x)-3(2-5x)(2+5x)$ |
| c) |
$(3x+4)^2-(3x-2)(3x-8)$ |
d) |
$(3x^2+2)(3x^2-2)(9x^4+4)$ |
| e) |
$(a+b)^2+(a-b)^2$ |
|
| a) |
$-5x^2+20$ |
b) |
$10x-11$ |
| c) |
$54x$ |
d) |
$81x^8-16$ |
| e) |
$2a^2+2b^2$ |
|
Övning 2.1:3
Faktorisera så långt som möjligt
| a) |
$x^2-36$ |
b) |
$5x^2-20$ |
c) |
$x^2+6x+9$ |
| d) |
$x^2-10x+25$ |
e) |
$18x-2x^3$ |
f) |
$16x^2+8x+1$ |
|
| a) |
$(x+6)(x-6)$ |
b) |
$5(x+2)(x-2)$ |
c) |
$(x+3)^2$ |
| d) |
$(x-5)^2$ |
e) |
$-2x(x+3)(x-3)$ |
f) |
$(4x+1)^2$ |
|
Övning 2.1:4
Bestäm koefficienterna framför $\,x\,$ och $\,x^2\,$ när följande uttryck utvecklas
| a) |
$(x+2)(3x^2-x+5)$ |
| b) |
$(1+x+x^2+x^3)(2-x+x^2+x^4)$ |
| c) |
$(x-x^3+x^5)(1+3x+5x^2)(2-7x^2-x^4)$ |
|
| a) |
$5\,$ framför $\,x^2\,$, $\,3\,$ framför $\,x$ |
| b) |
$2\,$ framför $\,x^2\,$, $\,1\,$ framför $\,x$ |
| $\textrm{c) }$ |
$6\,$ framför $\,x^2\,$, $\,2\,$ framför $\,x$ |
|
Övning 2.1:5
Förenkla så långt som möjligt
| a) |
$\displaystyle \frac{1}{x-x^2}-\displaystyle \frac{1}{x}$ |
b) |
$\displaystyle \frac{1}{y^2-2y}-\displaystyle \frac{2}{y^2-4}$ |
| c) |
$\displaystyle \frac{(3x^2-12)(x^2-1)}{(x+1)(x+2)}$ |
d) |
$\displaystyle \frac{(y^2+4y+4)(2y-4)}{(y^2+4)(y^2-4)}$ |
| a) |
$\displaystyle \frac{1}{1-x}$ |
b) |
$-\displaystyle \frac{1}{y(y+2)}$ |
| c) |
$3(x-2)(x-1)$ |
d) |
$\displaystyle \frac{2(y+2)}{y^2+4}$ |
Övning 2.1:6
Förenkla så långt som möjligt
| a) |
$\left(x-y+\displaystyle\frac{x^2}{y-x}\right)$ $\left(\displaystyle\frac{y}{2x-y}-1\right)$ |
b) |
$\displaystyle \frac{x}{x-2}+\displaystyle \frac{x}{x+3}-2$ |
| c) |
$\displaystyle \frac{2a+b}{a^2-ab}-\frac{2}{a-b}$ |
d) |
$\displaystyle\frac{a-b+\displaystyle\frac{b^2}{a+b}}{1-\left(\displaystyle\frac{a-b}{a+b}\right)^2}$ |
|
| a) |
$2y$ |
b) |
$\displaystyle\frac{-x+12}{(x-2)(x+3)}$ |
| c) |
$\displaystyle\frac{b}{a(a-b)}$ |
d) |
$\displaystyle\frac{a(a+b)}{4b}$ |
Övning 2.1:7
Förenkla följande bråkuttryck genom att skriva på gemensamt bråkstreck
| a) |
$\displaystyle \frac{2}{x+3}-\frac{2}{x+5}$ |
b) |
$x+\displaystyle \frac{1}{x-1}+\displaystyle \frac{1}{x^2}$ |
c) |
$\displaystyle \frac{ax}{a+1}-\displaystyle \frac{ax^2}{(a+1)^2}$ |
| a) |
$\displaystyle \frac{4}{(x+3)(x+5)}$ |
b) |
$\displaystyle \frac{x^4-x^3+x^2+x-1}{x^2(x-1)}$ |
c) |
$\displaystyle \frac{ax(a+1-x)}{(a+1)^2}$ |
Övning 2.1:8
Förenkla följande bråkuttryck genom att skriva på gemensamt bråkstreck
| a) |
$\displaystyle \frac{\displaystyle\ \frac{x}{x+1}\ }{\ 3+x\ }$ |
b) |
$\displaystyle \frac{\displaystyle \frac{3}{x}-\displaystyle \frac{1}{x}}{\displaystyle \frac{1}{x-3}}$ |
c) |
$\displaystyle \frac{1}{1+\displaystyle \frac{1}{1+\displaystyle \frac{1}{1+x}}}$ |
|
| a) |
$\displaystyle \frac{x}{(x+3)(x+1)}$ |
b) |
$\displaystyle \frac{2(x-3)}{x}$ |
c) |
$\displaystyle \frac{x+2}{2x+3}$ |
|
Övning 2.2:1
Lös ekvationerna
| a) |
$x-2=-1$ |
b) |
$2x+1=13$ |
| c) |
$\displaystyle\frac{1}{3}x-1=x$ |
d) |
$5x+7=2x-6$ |
|
| a) |
$x=1$ |
b) |
$x=6$ |
| c) |
$x=-\displaystyle\frac{3}{2}$ |
d) |
$x=-\displaystyle\frac{13}{3}$ |
|
Övning 2.2:2
Lös ekvationerna
| a) |
$\displaystyle\frac{5x}{6}-\displaystyle\frac{x+2}{9}=\displaystyle\frac{1}{2}$ |
b) |
$\displaystyle\frac{8x+3}{7}-\displaystyle\frac{5x-7}{4}=2$ |
| c) |
$(x+3)^2-(x-5)^2=6x+4$ |
d) |
$(x^2+4x+1)^2+3x^4-2x^2=(2x^2+2x+3)^2$ |
|
| a) |
$x=1$ |
b) |
$x=\displaystyle\frac{5}{3}$ |
| c) |
$x=2$ |
d) |
$x=-2$ |
|
Övning 2.2:3
Lös ekvationerna
| a) |
$\displaystyle\frac{x+3}{x-3}-\displaystyle\frac{x+5}{x-2}=0$ |
| b) |
$\displaystyle\frac{4x}{4x-7}-\displaystyle\frac{1}{2x-3}=1$ |
| c) |
$\left(\displaystyle\frac{1}{x-1}-\frac{1}{x+1}\right)\left(x^2+\frac{1}{2}\right)=\displaystyle\frac{6x-1}{3x-3}$ |
| d) |
$\left(\displaystyle\frac{2}{x}-3\right)\left(\displaystyle\frac{1}{4x}+\frac{1}{2}\right)-\left(\displaystyle\frac{1}{2x}-\frac{2}{3}\right)^2-\left(\displaystyle\frac{1}{2x}+\frac{1}{3}\right)\left(\displaystyle\frac{1}{2x}-\frac{1}{3}\right)=0$ |
|
| a) |
$x=9$ |
| b) |
$x=\displaystyle\frac{7}{5}$ |
| c) |
$x=\displaystyle\frac{4}{5}$ |
| d) |
$x=\displaystyle\frac{1}{2}$ |
|
Övning 2.2:4
| a) |
Skriv ekvationen för linjen $\,y=2x+3\,$ på formen $\,ax+by=c\,$. |
| b) |
Skriv ekvationen för linjen $\,3x+4y-5=0\,$ på formen $\,y=kx+m\,$. |
|
| a) |
$-2x+y=3$ |
| b) |
$y=-\displaystyle\frac{3}{4}x+\frac{5}{4}$ |
|
Övning 2.2:5
| a) |
Bestäm ekvationen för den räta linje som går genom punkterna $\,(2,3)\,$ och $\,(3,0)\,$. |
| b) |
Bestäm ekvationen för den räta linje som har riktningskoefficient $\,-3\,$ och går genom punkten $\,(1,-2)\,$. |
| c) |
Bestäm ekvationen för den räta linje som går genom punkten $\,(-1,2)\,$ och är parallell med linjen $\,y=3x+1\,$. |
| d) |
Bestäm ekvationen för den räta linje som går genom punkten $\,(2,4)\,$ och är vinkelrät mot linjen $\,y=2x+5\,$. |
| e) |
Bestäm riktningskoefficienten, $\,k\,$, för den räta linje som skär x-axeln i punkten $\,(5,0)\,$ och y-axeln i punkten $\,(0,-8)\,$. |
|
| a) |
$y=-3x+9$ |
| b) |
$y=-3x+1$ |
| c) |
$y=3x+5$ |
| d) |
$y=-\displaystyle \frac{1}{2}x+5$ |
| e) |
$k = \displaystyle\frac{8}{5}$ |
|
Övning 2.2:6
Finn skärningspunkten mellan följande linjer
| a) |
$y=3x+5\ $ och x-axeln |
b) |
$y=-x+5\ $ och y-axeln |
| c) |
$4x+5y+6=0\ $ och y-axeln |
d) |
$x+y+1=0\ $ och $\ x=12$ |
| e) |
$2x+y-1=0\ $ och $\ y-2x-2=0$ |
|
| a) |
$\bigl(-\frac{5}{3},0\bigr)$ |
b) |
$(0,5)$ |
| c) |
$\bigl(0,-\frac{6}{5}\bigr)$ |
d) |
$(12,-13)$ |
| e) |
$\bigl(-\frac{1}{4},\frac{3}{2}\bigr)$ |
|
Övning 2.2:7
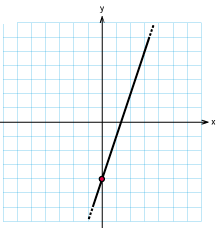
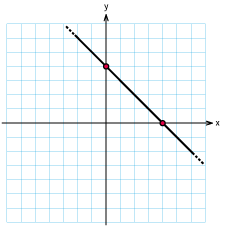
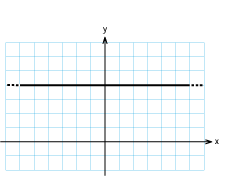
Skissera grafen till följande funktioner
| a) |
$f(x)=3x-2$ |
b) |
$f(x)=2-x$ |
c) |
$f(x)=2$ |
|
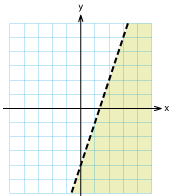
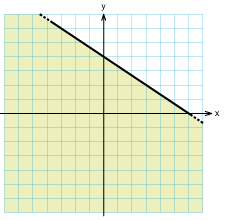
Övning 2.2:8
Rita in i ett xy-plan alla punkter vars koordinater $\,(x,y)\,$ uppfyller
| a) |
$y \geq x $ |
b) |
$y < 3x -4 $ |
c) |
$2x+3y \leq 6 $ |
|
Övning 2.2:9
Beräkna arean av den triangel som
| a) |
har hörn i punkterna $\,(1,4)\,$, $\,(3,3)\,$ och $\,(1,0)\,$ |
| b) |
begränsas av linjerna $\ x=2y\,$, $\ y=4\ $ och $\ y=10-2x\,$ |
| c) |
beskrivs av olikheterna $\ x+y \geq -2\,$, $\ 2x-y \leq 2\ $ och $\ 2y-x \leq 2\,$ |
|
| a) |
$4\,$ a.e. |
| b) |
$5\,$ a.e. |
| c) |
$6\,$ a.e. |
|