Sommarmatte 1
(Skillnad mellan versioner)
Versionen från 21 juni 2007 kl. 15.23 (redigera)
KTH.SE:u1xsetv1 (Diskussion | bidrag)
← Gå till föregående ändring |
Nuvarande version (25 juni 2007 kl. 12.10) (redigera) (ogör)
KTH.SE:u1xsetv1 (Diskussion | bidrag)
|
| (3 mellanliggande versioner visas inte.) |
| Rad 1: |
Rad 1: |
| | + | __NOTOC__ |
| | + | |
| | ==Övning 2.1:1== | | ==Övning 2.1:1== |
| | <div class="ovning"> | | <div class="ovning"> |
| Rad 966: |
Rad 968: |
| | </div> | | </div> |
| | | | |
| - | <div class=NavFrame style="CLEAR: both"> | + | <div class="svar"> |
| - | <div class=NavHead>Facit </div> | + | |
| - | <div class=NavContent> | + | |
| - | Facit till alla delfrågor<br \> | + | |
| | <table width="100%" cellspacing="10px"> | | <table width="100%" cellspacing="10px"> |
| | <tr align="left"> | | <tr align="left"> |
| - | <td>Se lösningarna.</td> | + | <td>Se lösningen i |
| | + | webmaterialet när du loggat in till kursen.</td> |
| | </tr> | | </tr> |
| | </table> | | </table> |
| - | </div> | |
| - | </div> | |
| - | | |
| - | <div class=NavFrame style="CLEAR: both"> | |
| - | <div class=NavHead>Lösning a) </div> | |
| - | <div class=NavContent> | |
| - | Lösning till delfråga a) | |
| - | <table width="100%" cellspacing="10px"> | |
| - | <tr> | |
| - | <td align="center"> | |
| - | [[Bild:2_3_8a.gif]] | |
| - | </td> | |
| - | </tr> | |
| - | </table> | |
| - | </div> | |
| - | </div> | |
| - | | |
| - | | |
| - | <div class=NavFrame style="CLEAR: both"> | |
| - | <div class=NavHead>Lösning b) </div> | |
| - | <div class=NavContent> | |
| - | Lösning till delfråga b) | |
| - | <table width="100%" cellspacing="10px"> | |
| - | <tr> | |
| - | <td align="center"> | |
| - | [[Bild:2_3_8b.gif]] | |
| - | </td> | |
| - | </tr> | |
| - | </table> | |
| - | </div> | |
| - | </div> | |
| - | | |
| - | | |
| - | <div class=NavFrame style="CLEAR: both"> | |
| - | <div class=NavHead>Lösning c) </div> | |
| - | <div class=NavContent> | |
| - | Lösning till delfråga c) | |
| - | <table width="100%" cellspacing="10px"> | |
| - | <tr> | |
| - | <td align="center"> | |
| - | [[Bild:2_3_8c.gif]] | |
| - | </td> | |
| - | </tr> | |
| - | </table> | |
| - | </div> | |
| | </div> | | </div> |
| | | | |
| Rad 1 074: |
Rad 1 029: |
| | </div> | | </div> |
| | | | |
| - | <div class=NavFrame style="CLEAR: both"> | + | <div class="svar"> |
| - | <div class=NavHead>Facit </div> | + | |
| - | <div class=NavContent> | + | |
| - | Facit till alla delfrågor | + | |
| | <table width="100%" cellspacing="10px"> | | <table width="100%" cellspacing="10px"> |
| | <tr align="left"> | | <tr align="left"> |
| - | <td>Se lösningarna.</td> | + | <td>Se lösningen i webmaterialet när du loggat in till kursen</td> |
| | </tr> | | </tr> |
| | </table> | | </table> |
| - | </div> | |
| - | </div> | |
| - | | |
| - | <div class=NavFrame style="CLEAR: both"> | |
| - | <div class=NavHead>Lösning a) </div> | |
| - | <div class=NavContent> | |
| - | Lösning till delfråga a) | |
| - | <table width="100%" cellspacing="10px"> | |
| - | <tr> | |
| - | <td align="center"> | |
| - | [[Bild:2_3_10a.gif]] | |
| - | </td> | |
| - | </tr> | |
| - | </table> | |
| - | </div> | |
| - | </div> | |
| - | | |
| - | <div class=NavFrame style="CLEAR: both"> | |
| - | <div class=NavHead>Lösning b) </div> | |
| - | <div class=NavContent> | |
| - | Lösning till delfråga b) | |
| - | <table width="100%" cellspacing="10px"> | |
| - | <tr> | |
| - | <td align="center"> | |
| - | [[Bild:2_3_10b-1(3).gif]] | |
| - | </td> | |
| - | </tr> | |
| - | <tr> | |
| - | <td align="center"> | |
| - | [[Bild:2_3_10b-2(3).gif]] | |
| - | </td> | |
| - | </tr> | |
| - | <tr> | |
| - | <td align="center"> | |
| - | [[Bild:2_3_10b-3(3).gif]] | |
| - | </td> | |
| - | </tr> | |
| - | </table> | |
| - | </div> | |
| - | </div> | |
| - | | |
| - | <div class=NavFrame style="CLEAR: both"> | |
| - | <div class=NavHead>Lösning c) </div> | |
| - | <div class=NavContent> | |
| - | Lösning till delfråga c) | |
| - | <table width="100%" cellspacing="10px"> | |
| - | <tr> | |
| - | <td align="center"> | |
| - | [[Bild:2_3_10c-1(2).gif]] | |
| - | </td> | |
| - | </tr> | |
| - | <tr> | |
| - | <td align="center"> | |
| - | [[Bild:2_3_10c-2(2).gif]] | |
| - | </td> | |
| - | </tr> | |
| - | </table> | |
| - | </div> | |
| - | </div> | |
| - | | |
| - | <div class=NavFrame style="CLEAR: both"> | |
| - | <div class=NavHead>Lösning d) </div> | |
| - | <div class=NavContent> | |
| - | Lösning till delfråga d) | |
| - | <table width="100%" cellspacing="10px"> | |
| - | <tr> | |
| - | <td align="center"> | |
| - | [[Bild:2_3_10d.gif]] | |
| - | </td> | |
| - | </tr> | |
| - | </table> | |
| - | </div> | |
| | </div> | | </div> |
Nuvarande version
Utveckla
| a) |
$3x(x-1)$ |
b) |
$(1+x-x^2)xy$ |
c) |
$-x^2(4-y^2)$ |
| d) |
$x^3y^2\left(\displaystyle \frac{1}{y} - \frac{1}{xy}+1\right)$ |
e) |
$(x-7)^2$ |
f) |
$(5+4y)^2$ |
| g) |
$(y^2-3x^3)^2$ |
h) |
$(5x^3+3x^5)^2$ |
|
| a) |
$3x^2-3x$ |
b) |
$xy+x^2y-x^3y$ |
c) |
$-4x^2+x^2y^2$ |
| d) |
$x^3y-x^2y+x^3y^2$ |
e) |
$x^2-14x+49$ |
f) |
$16y^2+40y+25$ |
| g) |
$9x^6-6x^3y^2+y^4$ |
h) |
$9x^{10}+30x^8+25x^6$ |
|
Utveckla och förenkla så långt som möjligt
| a) |
$(x-4)(x-5)-3x(2x-3)$ |
b) |
$(1-5x)(1+15x)-3(2-5x)(2+5x)$ |
| c) |
$(3x+4)^2-(3x-2)(3x-8)$ |
d) |
$(3x^2+2)(3x^2-2)(9x^4+4)$ |
| e) |
$(a+b)^2+(a-b)^2$ |
|
| a) |
$-5x^2+20$ |
b) |
$10x-11$ |
| c) |
$54x$ |
d) |
$81x^8-16$ |
| e) |
$2a^2+2b^2$ |
|
Faktorisera så långt som möjligt
| a) |
$x^2-36$ |
b) |
$5x^2-20$ |
c) |
$x^2+6x+9$ |
| d) |
$x^2-10x+25$ |
e) |
$18x-2x^3$ |
f) |
$16x^2+8x+1$ |
|
| a) |
$(x+6)(x-6)$ |
b) |
$5(x+2)(x-2)$ |
c) |
$(x+3)^2$ |
| d) |
$(x-5)^2$ |
e) |
$-2x(x+3)(x-3)$ |
f) |
$(4x+1)^2$ |
|
Bestäm koefficienterna framför $\,x\,$ och $\,x^2\,$ när följande uttryck utvecklas
| a) |
$(x+2)(3x^2-x+5)$ |
| b) |
$(1+x+x^2+x^3)(2-x+x^2+x^4)$ |
| c) |
$(x-x^3+x^5)(1+3x+5x^2)(2-7x^2-x^4)$ |
|
| a) |
$5\,$ framför $\,x^2\,$, $\,3\,$ framför $\,x$ |
| b) |
$2\,$ framför $\,x^2\,$, $\,1\,$ framför $\,x$ |
| $\textrm{c) }$ |
$6\,$ framför $\,x^2\,$, $\,2\,$ framför $\,x$ |
|
Förenkla så långt som möjligt
| a) |
$\displaystyle \frac{1}{x-x^2}-\displaystyle \frac{1}{x}$ |
b) |
$\displaystyle \frac{1}{y^2-2y}-\displaystyle \frac{2}{y^2-4}$ |
| c) |
$\displaystyle \frac{(3x^2-12)(x^2-1)}{(x+1)(x+2)}$ |
d) |
$\displaystyle \frac{(y^2+4y+4)(2y-4)}{(y^2+4)(y^2-4)}$ |
| a) |
$\displaystyle \frac{1}{1-x}$ |
b) |
$-\displaystyle \frac{1}{y(y+2)}$ |
| c) |
$3(x-2)(x-1)$ |
d) |
$\displaystyle \frac{2(y+2)}{y^2+4}$ |
Förenkla så långt som möjligt
| a) |
$\left(x-y+\displaystyle\frac{x^2}{y-x}\right)$ $\left(\displaystyle\frac{y}{2x-y}-1\right)$ |
b) |
$\displaystyle \frac{x}{x-2}+\displaystyle \frac{x}{x+3}-2$ |
| c) |
$\displaystyle \frac{2a+b}{a^2-ab}-\frac{2}{a-b}$ |
d) |
$\displaystyle\frac{a-b+\displaystyle\frac{b^2}{a+b}}{1-\left(\displaystyle\frac{a-b}{a+b}\right)^2}$ |
|
| a) |
$2y$ |
b) |
$\displaystyle\frac{-x+12}{(x-2)(x+3)}$ |
| c) |
$\displaystyle\frac{b}{a(a-b)}$ |
d) |
$\displaystyle\frac{a(a+b)}{4b}$ |
Förenkla följande bråkuttryck genom att skriva på gemensamt bråkstreck
| a) |
$\displaystyle \frac{2}{x+3}-\frac{2}{x+5}$ |
b) |
$x+\displaystyle \frac{1}{x-1}+\displaystyle \frac{1}{x^2}$ |
c) |
$\displaystyle \frac{ax}{a+1}-\displaystyle \frac{ax^2}{(a+1)^2}$ |
| a) |
$\displaystyle \frac{4}{(x+3)(x+5)}$ |
b) |
$\displaystyle \frac{x^4-x^3+x^2+x-1}{x^2(x-1)}$ |
c) |
$\displaystyle \frac{ax(a+1-x)}{(a+1)^2}$ |
Förenkla följande bråkuttryck genom att skriva på gemensamt bråkstreck
| a) |
$\displaystyle \frac{\displaystyle\ \frac{x}{x+1}\ }{\ 3+x\ }$ |
b) |
$\displaystyle \frac{\displaystyle \frac{3}{x}-\displaystyle \frac{1}{x}}{\displaystyle \frac{1}{x-3}}$ |
c) |
$\displaystyle \frac{1}{1+\displaystyle \frac{1}{1+\displaystyle \frac{1}{1+x}}}$ |
|
| a) |
$\displaystyle \frac{x}{(x+3)(x+1)}$ |
b) |
$\displaystyle \frac{2(x-3)}{x}$ |
c) |
$\displaystyle \frac{x+2}{2x+3}$ |
|
Lös ekvationerna
| a) |
$x-2=-1$ |
b) |
$2x+1=13$ |
| c) |
$\displaystyle\frac{1}{3}x-1=x$ |
d) |
$5x+7=2x-6$ |
|
| a) |
$x=1$ |
b) |
$x=6$ |
| c) |
$x=-\displaystyle\frac{3}{2}$ |
d) |
$x=-\displaystyle\frac{13}{3}$ |
|
Lös ekvationerna
| a) |
$\displaystyle\frac{5x}{6}-\displaystyle\frac{x+2}{9}=\displaystyle\frac{1}{2}$ |
b) |
$\displaystyle\frac{8x+3}{7}-\displaystyle\frac{5x-7}{4}=2$ |
| c) |
$(x+3)^2-(x-5)^2=6x+4$ |
d) |
$(x^2+4x+1)^2+3x^4-2x^2=(2x^2+2x+3)^2$ |
|
| a) |
$x=1$ |
b) |
$x=\displaystyle\frac{5}{3}$ |
| c) |
$x=2$ |
d) |
$x=-2$ |
|
Lös ekvationerna
| a) |
$\displaystyle\frac{x+3}{x-3}-\displaystyle\frac{x+5}{x-2}=0$ |
| b) |
$\displaystyle\frac{4x}{4x-7}-\displaystyle\frac{1}{2x-3}=1$ |
| c) |
$\left(\displaystyle\frac{1}{x-1}-\frac{1}{x+1}\right)\left(x^2+\frac{1}{2}\right)=\displaystyle\frac{6x-1}{3x-3}$ |
| d) |
$\left(\displaystyle\frac{2}{x}-3\right)\left(\displaystyle\frac{1}{4x}+\frac{1}{2}\right)-\left(\displaystyle\frac{1}{2x}-\frac{2}{3}\right)^2-\left(\displaystyle\frac{1}{2x}+\frac{1}{3}\right)\left(\displaystyle\frac{1}{2x}-\frac{1}{3}\right)=0$ |
|
| a) |
$x=9$ |
| b) |
$x=\displaystyle\frac{7}{5}$ |
| c) |
$x=\displaystyle\frac{4}{5}$ |
| d) |
$x=\displaystyle\frac{1}{2}$ |
|
| a) |
Skriv ekvationen för linjen $\,y=2x+3\,$ på formen $\,ax+by=c\,$. |
| b) |
Skriv ekvationen för linjen $\,3x+4y-5=0\,$ på formen $\,y=kx+m\,$. |
|
| a) |
$-2x+y=3$ |
| b) |
$y=-\displaystyle\frac{3}{4}x+\frac{5}{4}$ |
|
| a) |
Bestäm ekvationen för den räta linje som går genom punkterna $\,(2,3)\,$ och $\,(3,0)\,$. |
| b) |
Bestäm ekvationen för den räta linje som har riktningskoefficient $\,-3\,$ och går genom punkten $\,(1,-2)\,$. |
| c) |
Bestäm ekvationen för den räta linje som går genom punkten $\,(-1,2)\,$ och är parallell med linjen $\,y=3x+1\,$. |
| d) |
Bestäm ekvationen för den räta linje som går genom punkten $\,(2,4)\,$ och är vinkelrät mot linjen $\,y=2x+5\,$. |
| e) |
Bestäm riktningskoefficienten, $\,k\,$, för den räta linje som skär x-axeln i punkten $\,(5,0)\,$ och y-axeln i punkten $\,(0,-8)\,$. |
|
| a) |
$y=-3x+9$ |
| b) |
$y=-3x+1$ |
| c) |
$y=3x+5$ |
| d) |
$y=-\displaystyle \frac{1}{2}x+5$ |
| e) |
$k = \displaystyle\frac{8}{5}$ |
|
Finn skärningspunkten mellan följande linjer
| a) |
$y=3x+5\ $ och x-axeln |
b) |
$y=-x+5\ $ och y-axeln |
| c) |
$4x+5y+6=0\ $ och y-axeln |
d) |
$x+y+1=0\ $ och $\ x=12$ |
| e) |
$2x+y-1=0\ $ och $\ y-2x-2=0$ |
|
| a) |
$\bigl(-\frac{5}{3},0\bigr)$ |
b) |
$(0,5)$ |
| c) |
$\bigl(0,-\frac{6}{5}\bigr)$ |
d) |
$(12,-13)$ |
| e) |
$\bigl(-\frac{1}{4},\frac{3}{2}\bigr)$ |
|
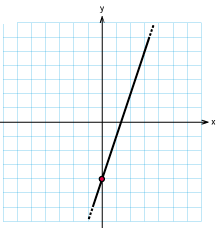
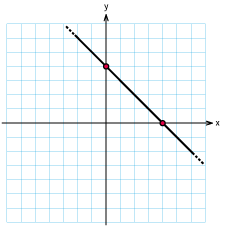
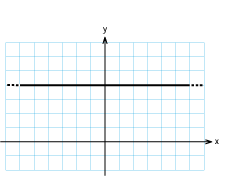
Skissera grafen till följande funktioner
| a) |
$f(x)=3x-2$ |
b) |
$f(x)=2-x$ |
c) |
$f(x)=2$ |
|
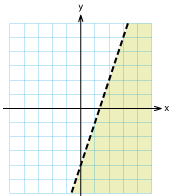
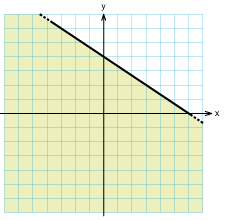
Rita in i ett xy-plan alla punkter vars koordinater $\,(x,y)\,$ uppfyller
| a) |
$y \geq x $ |
b) |
$y < 3x -4 $ |
c) |
$2x+3y \leq 6 $ |
|
Beräkna arean av den triangel som
| a) |
har hörn i punkterna $\,(1,4)\,$, $\,(3,3)\,$ och $\,(1,0)\,$ |
| b) |
begränsas av linjerna $\ x=2y\,$, $\ y=4\ $ och $\ y=10-2x\,$ |
| c) |
beskrivs av olikheterna $\ x+y \geq -2\,$, $\ 2x-y \leq 2\ $ och $\ 2y-x \leq 2\,$ |
|
| a) |
$4\,$ a.e. |
| b) |
$5\,$ a.e. |
| c) |
$6\,$ a.e. |
|
Kvadratkomplettera följande uttryck
| a) |
$x^2-2x$ |
b) |
$x^2+2x-1$ |
c) |
$5+2x-x^2$ |
d) |
$x^2+5x+3$ |
|
| a) |
$(x-1)^2-1$ |
b) |
$(x+1)^2-2$ |
c) |
$-(x-1)^2+6$ |
d) |
$\bigl(x+\frac{5}{2}\bigr)^2-\frac{13}{4}$ |
|
Lös följande andragradsekvationer med kvadratkomplettering
| a) |
$x^2-4x+3=0$ |
b) |
$y^2+2y-15=0$ |
c) |
$y^2+3y+4=0$ |
| d) |
$4x^2-28x+13=0$ |
e) |
$5x^2+2x-3=0$ |
f) |
$3x^2-10x+8=0$ |
|
|
| a) |
$\left\{ \eqalign{ x_1 &= 1 \cr x_2 &= 3\cr }\right.$ |
b) |
$\left\{ \eqalign{ y_1 &= -5 \cr y_2 &= 3\cr }\right.$ |
c) |
saknar (reella) lösning |
| d) |
$ \left\{ \eqalign{ x_1 &= \textstyle\frac{1}{2}\cr x_2 &= \textstyle\frac{13}{2}\cr }\right.$ |
e) |
$\left\{ \eqalign{ x_1 &= -1 \cr x_2 &= \textstyle\frac{3}{5}\cr }\right.$ |
f) |
$ \left\{ \eqalign{ x_1 &= \textstyle\frac{4}{3}\cr x_2 &= 2\cr }\right.$ |
|
Lös följande ekvationer direkt
| a) |
$x(x+3)=0$ |
b) |
$(x-3)(x+5)=0$ |
| c) |
$5(3x-2)(x+8)=0$ |
d) |
$x(x+3)-x(2x-9)=0$ |
| e) |
$(x+3)(x-1)-(x+3)(2x-9)=0$ |
f) |
$x(x^2-2x)+x(2-x)=0$ |
|
| a) |
$\left\{ \eqalign{ x_1 &= 0 \cr x_2 & = -3\cr }\right.$ |
b) |
$\left\{ \eqalign{ x_1 &= 3 \cr x_2 & = -5\cr }\right. $ |
| c) |
$\left\{ \eqalign{ x_1 & = \textstyle\frac{2}{3} \cr x_2 & = -8\cr }\right. $ |
d) |
$\left\{ \eqalign{ x_1 & = 0\cr x_2 & = 12\cr }\right. $ |
| e) |
$\left\{ \eqalign{ x_1 & = -3 \cr x_2 & = 8\cr }\right. $ |
f) |
$\left\{ \eqalign{ x_1 & = 0 \cr x_2 & = 1 \cr x_3 & = 2 }\right. $ |
|
Bestäm en andragradsekvation som har rötterna
| a) |
$-1\ $ och $\ 2$ |
| b) |
$1+\sqrt{3}\ $ och $\ 1-\sqrt{3}$ |
| c) |
$3\ $ och $\ \sqrt{3}$ |
|
| a) |
$ax^2-ax-2a=0\,$, där $\,a\ne 0\,$ är en konstant. |
| b) |
$ax^2-2ax-2a=0\,$, där $\,a\ne 0\,$ är en konstant. |
| c) |
$ax^2-(3+\sqrt{3}\,)ax+3\sqrt{3}\,a=0\,$, där $\,a\ne 0\,$ är en konstant. |
|
| a) |
Bestäm en andragradsekvation som bara har $\,-7\,$ som rot. |
| b) |
Bestäm ett värde på $\,x\,$ som gör att uttrycket $\,4x^2-28x+48\,$ är negativt. |
| c) |
Ekvationen $\,x^2+4x+b=0\,$ har en rot $\,x=1\,$. Bestäm värdet på konstanten $\,b\,$. |
|
| a) |
Exempelvis $\ x^2+14x+49=0\,$. |
| b) |
$3< x<4$ |
| c) |
$b=-5$ |
|
Bestäm det minsta värde som följande polynom antar
| a) |
$x^2-2x+1$ |
b) |
$x^2-4x+2$ |
c) |
$x^2-5x+7$ |
|
| a) |
$0$ |
b) |
$-2$ |
c) |
$\displaystyle \frac{3}{4}$ |
|
Bestäm det största värde som följande polynom antar
| a) |
$1-x^2$ |
b) |
$-x^2+3x-4$ |
c) |
$x^2+x+1$ |
|
| a) |
$1$ |
b) |
$\displaystyle -\frac{7}{4}$ |
c) |
saknar max |
|
Skissera grafen till följande funktioner
| a) |
$f(x)=x^2+1$ |
b) |
$f(x)=(x-1)^2+2$ |
c) |
$f(x)=x^2-6x+11$ |
|
| Se lösningen i
webmaterialet när du loggat in till kursen. |
Hitta alla skärningspunkter mellan x-axeln och kurvan
| a) |
$y=x^2-1$ |
b) |
$y=x^2-5x+6$ |
c) |
$y=3x^2-12x+9$ |
|
| a) |
$(-1,0)\ $ och $\ (1,0)$ |
b) |
$(2,0)\ $ och $\ (3,0)$ |
c) |
$(1,0)\ $ och $\ (3,0)$ |
|
Rita in i ett xy-plan alla punkter vars koordinater $\,(x,y)\,$ uppfyller
| a) |
$y \geq x^2\ $ och $\ y \leq 1 $ |
b) |
$y \leq 1-x^2\ $ och $\ x \geq 2y-3 $ |
| c) |
$1 \geq x \geq y^2 $ |
d) |
$x^2 \leq y \leq x $ |
|
| Se lösningen i webmaterialet när du loggat in till kursen |