Versionen från 25 juni 2007 kl. 08.08 (redigera)
KTH.SE:u1xsetv1 (Diskussion | bidrag)
← Gå till föregående ändring |
Nuvarande version (30 juni 2007 kl. 15.48) (redigera) (ogör)
KTH.SE:u1m1gion (Diskussion | bidrag)
|
| (28 mellanliggande versioner visas inte.) |
| Rad 187: |
Rad 187: |
| | </div> | | </div> |
| | | | |
| - | <div class=NavFrame style="CLEAR: both"> | + | <div class="svar"> |
| - | <div class=NavHead>Facit </div> | + | |
| - | <div class=NavContent> | + | |
| - | Facit till alla delfrågor<br \> | + | |
| | <table width="100%" cellspacing="10px"> | | <table width="100%" cellspacing="10px"> |
| | <tr align="left"> | | <tr align="left"> |
| | <td class="ntext">a)</td> | | <td class="ntext">a)</td> |
| - | <td class="ntext" width="50%">BILD</td> | + | <td class="ntext" width="50%">En cirkel med radie 3 och medelpunkt i origo.</td> |
| | <td class="ntext">b)</td> | | <td class="ntext">b)</td> |
| - | <td class="ntext" width="50%">BILD</td> | + | <td class="ntext" width="50%">En cirkel med radie $\sqrt 3$ och medelpunkt i punkten (1, 2).</td> |
| | </tr> | | </tr> |
| | <tr align="left"> | | <tr align="left"> |
| | <td class="ntext">c)</td> | | <td class="ntext">c)</td> |
| - | <td class="ntext" width="50%">BILD</td> | + | <td class="ntext" width="50%">En cirkel med radie $\frac{1}{3}\sqrt 10$ och medelpunkt i punkten (1/3, -7/3).</td> |
| | </tr> | | </tr> |
| | <tr><td height="5px"/></tr> | | <tr><td height="5px"/></tr> |
| | </table> | | </table> |
| - | </div> | |
| - | </div> | |
| - | | |
| - | <div class=NavFrame style="CLEAR: both"> | |
| - | <div class=NavHead>Lösning a) </div> | |
| - | <div class=NavContent> | |
| - | Lösning till delfråga a) | |
| - | <table width="100%"> | |
| - | <tr> | |
| - | <td align="center"> | |
| - | [[Bild:4_1_6a.gif]] | |
| - | </td> | |
| - | </tr> | |
| - | </table> | |
| - | | |
| - | </div> | |
| - | </div> | |
| - | | |
| - | <div class=NavFrame style="CLEAR: both"> | |
| - | <div class=NavHead>Lösning b) </DIV> | |
| - | <div class=NavContent> | |
| - | Lösning till delfråga b) | |
| - | <table width="100%"> | |
| - | <tr> | |
| - | <td align="center"> | |
| - | [[Bild:4_1_6b.gif]] | |
| - | </td> | |
| - | </tr> | |
| - | </table> | |
| - | </div> | |
| - | </div> | |
| - | | |
| - | <div class=NavFrame style="CLEAR: both"> | |
| - | <div class=NavHead>Lösning c) </DIV> | |
| - | <div class=NavContent> | |
| - | Lösning till delfråga c) | |
| - | <table width="100%"> | |
| - | <tr> | |
| - | <td align="center"> | |
| - | [[Bild:4_1_6c-1(2).gif]] | |
| - | </td> | |
| - | </tr> | |
| - | <tr> | |
| - | <td align="center"> | |
| - | [[Bild:4_1_6c-2(2).gif]] | |
| - | </td> | |
| - | </tr> | |
| - | </table> | |
| - | </div> | |
| | </div> | | </div> |
| | | | |
| Rad 275: |
Rad 223: |
| | </div> | | </div> |
| | | | |
| - | <div class=NavFrame style="CLEAR: both"> | + | <div class="svar"> |
| - | <div class=NavHead>Facit </div> | + | |
| - | <div class=NavContent> | + | |
| - | Facit till alla delfrågor<br \> | + | |
| | <table width="100%" cellspacing="10px"> | | <table width="100%" cellspacing="10px"> |
| | <tr align="left"> | | <tr align="left"> |
| | <td class="ntext">a)</td> | | <td class="ntext">a)</td> |
| - | <td class="ntext" width="50%">BILD</td> | + | <td class="ntext" width="50%">En cirkel med medelpunkt (-1, 1) och radie $\sqrt 3$.</td> |
| | <td class="ntext">b)</td> | | <td class="ntext">b)</td> |
| - | <td class="ntext" width="50%">BILD</td> | + | <td class="ntext" width="50%">En cirkel med medelpunkt (0, -2) och radie 2. </td> |
| | </tr> | | </tr> |
| | <tr align="left"> | | <tr align="left"> |
| | <td class="ntext">c)</td> | | <td class="ntext">c)</td> |
| - | <td class="ntext" width="50%">BILD</td> | + | <td class="ntext" width="50%">En cirkel med medelpunkt (1, -3) och radie $\sqrt 7$.</td> |
| | + | </tr> |
| | + | <tr align="left"> |
| | <td class="ntext">d)</td> | | <td class="ntext">d)</td> |
| - | <td class="ntext" width="50%">BILD</td> | + | <td class="ntext" width="50%">Endast punkten (1, -1). </td> |
| | </tr> | | </tr> |
| | + | |
| | <tr><td height="5px"/></tr> | | <tr><td height="5px"/></tr> |
| | </table> | | </table> |
| - | </div> | |
| - | </div> | |
| - | | |
| - | <div class=NavFrame style="CLEAR: both"> | |
| - | <div class=NavHead>Lösning a) </div> | |
| - | <div class=NavContent> | |
| - | Lösning till delfråga a) | |
| - | <table width="100%"> | |
| - | <tr> | |
| - | <td align="center"> | |
| - | [[Bild:4_1_7a-1(2).gif]] | |
| - | </td> | |
| - | </tr> | |
| - | <tr> | |
| - | <td align="center"> | |
| - | [[Bild:4_1_7a-2(2).gif]] | |
| - | </td> | |
| - | </tr> | |
| - | </table> | |
| - | | |
| - | </div> | |
| - | </div> | |
| - | | |
| - | <div class=NavFrame style="CLEAR: both"> | |
| - | <div class=NavHead>Lösning b) </DIV> | |
| - | <div class=NavContent> | |
| - | Lösning till delfråga b) | |
| - | <table width="100%"> | |
| - | <tr> | |
| - | <td align="center"> | |
| - | [[Bild:4_1_7b.gif]] | |
| - | </td> | |
| - | </tr> | |
| - | </table> | |
| - | </div> | |
| - | </div> | |
| - | | |
| - | <div class=NavFrame style="CLEAR: both"> | |
| - | <div class=NavHead>Lösning c) </DIV> | |
| - | <div class=NavContent> | |
| - | Lösning till delfråga c) | |
| - | <table width="100%"> | |
| - | <tr> | |
| - | <td align="center"> | |
| - | [[Bild:4_1_7c.gif]] | |
| - | </td> | |
| - | </tr> | |
| - | </table> | |
| - | </div> | |
| - | </div> | |
| - | | |
| - | <div class=NavFrame style="CLEAR: both"> | |
| - | <div class=NavHead>Lösning d) </DIV> | |
| - | <div class=NavContent> | |
| - | Lösning till delfråga d) | |
| - | <table width="100%"> | |
| - | <tr> | |
| - | <td align="center"> | |
| - | [[Bild:4_1_7d.gif]] | |
| - | </td> | |
| - | </tr> | |
| - | </table> | |
| - | </div> | |
| | </div> | | </div> |
| | | | |
| Rad 397: |
Rad 282: |
| | <table width="100%" cellspacing="10px"> | | <table width="100%" cellspacing="10px"> |
| | <tr><td height="5px"/></tr> | | <tr><td height="5px"/></tr> |
| - | <tr align="center"> | + | <tr> |
| - | <td class="ntext" width="100%">BILD</td> | + | <td align="center"> |
| - | </tr> | + | [[Bild:Uppg_4_1_10.gif]] |
| - | <tr><td height="5px"/></tr> | + | </td> |
| | + | </tr><tr><td height="5px"/></tr> |
| | </table> | | </table> |
| | + | |
| | | | |
| | </div> | | </div> |
| Rad 695: |
Rad 582: |
| | </div> | | </div> |
| | | | |
| - | <div class=NavFrame style="CLEAR: both"> | + | <div class="svar"> |
| - | <div class=NavHead>Facit </div> | + | |
| - | <div class=NavContent> | + | |
| | <table width="100%" cellspacing="10px"> | | <table width="100%" cellspacing="10px"> |
| | <tr align="left"> | | <tr align="left"> |
| Rad 705: |
Rad 590: |
| | </table> | | </table> |
| | </div> | | </div> |
| | + | |
| | + | ==Övning 4.2:9== |
| | + | <div class="ovning"> |
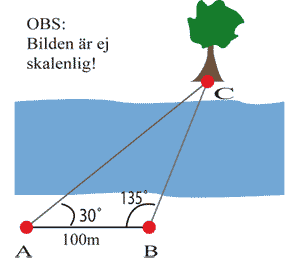
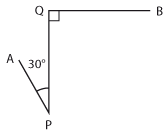
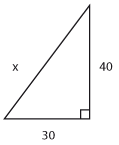
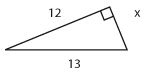
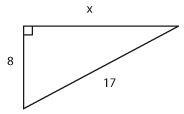
| | + | Bilvägen från ''A'' till ''B'' består av tre rätlinjiga delar ''AP'', ''PQ'' och ''QB'', vilka är 4,0 km, 12,0 km respektive 5,0 km. De i figuren markerade vinklarna vid ''P'' och ''Q'' är 30° respektive 90°. Beräkna avståndet fågelvägen från ''A'' till ''B''. (Uppgiften är hämtad ur Centrala provet i matematik, november 1976, men aningen modifierad.) |
| | + | <table width="100%" cellspacing="10px"> |
| | + | <tr align="center"> |
| | + | <td class="ntext" width="100%">[[Bild:O4_2_9.gif]]</td> |
| | + | </tr> |
| | + | <tr><td height="5px"/></tr> |
| | + | </table> |
| | </div> | | </div> |
| | | | |
| - | <div class=NavFrame style="CLEAR: both"> | + | <div class="svar"> |
| - | <div class=NavHead>Lösning </div> | + | <table width="100%" cellspacing="10px"> |
| - | <div class=NavContent> | + | <tr align="left"> |
| - | <table width="100%"> | + | <td class="ntext" width="100%">Avståndet är $\ \sqrt{205-48\sqrt{3}} \approx 11{,}0$ km.</td> |
| - | <tr> | + | |
| - | <td align="center"> | + | |
| - | [[Bild:4_2_8-1(2).gif]] | + | |
| - | </td> | + | |
| | </tr> | | </tr> |
| - | <tr> | + | <tr><td height="5px"/></tr> |
| - | <td align="center"> | + | </table> |
| - | [[Bild:4_2_8-2(2).gif]] | + | </div> |
| | + | |
| | + | ==Övning 4.3:1== |
| | + | <div class="ovning"> |
| | + | Bestäm de vinklar $\,v\,$ mellan $\,\displaystyle \frac{\pi}{2}\,$ och $\,2\pi\,$ som uppfyller |
| | + | <table width="100%" cellspacing="10px"> |
| | + | <tr align="left"> |
| | + | <td class="ntext">a)</td> |
| | + | <td class="ntext" width="33%">$\cos{v}=\cos{\displaystyle \frac{\pi}{5}}$</td> |
| | + | <td class="ntext">b)</td> |
| | + | <td class="ntext" width="33%">$\sin{v}=\sin{\displaystyle \frac{\pi}{7}}$</td> |
| | + | <td class="ntext">c)</td> |
| | + | <td class="ntext" width="33%">$\tan{v}=\tan{\displaystyle \frac{2\pi}{7}}$</td> |
| | + | </tr> |
| | + | </table> |
| | + | </div> |
| | + | |
| | + | <div class="svar"> |
| | + | <table width="100%" cellspacing="10px"> |
| | + | <tr align="left"> |
| | + | <td class="ntext">a)</td> |
| | + | <td class="ntext" width="33%">$v = \displaystyle \frac{9\pi}{5}$</td> |
| | + | <td class="ntext">b)</td> |
| | + | <td class="ntext" width="33%">$v = \displaystyle \frac{6\pi}{7}$</td> |
| | + | <td class="ntext">c)</td> |
| | + | <td class="ntext" width="33%">$v = \displaystyle \frac{9\pi}{7}$</td> |
| | + | </tr> |
| | + | </table> |
| | + | </div> |
| | + | |
| | + | ==Övning 4.3:2== |
| | + | <div class="ovning"> |
| | + | Bestäm de vinklar $\,v\,$ mellan 0 och $\,\pi\,$ som uppfyller |
| | + | <table width="100%" cellspacing="10px"> |
| | + | <tr align="left"> |
| | + | <td class="ntext">a)</td> |
| | + | <td class="ntext" width="50%">$\cos{v} = \cos{\displaystyle \frac{3\pi}{2}}$</td> |
| | + | <td class="ntext">b)</td> |
| | + | <td class="ntext" width="50%">$\cos{v} = \cos{ \displaystyle \frac{7\pi}{5}}$</td> |
| | + | </tr> |
| | + | <tr><td height="5px"/></tr> |
| | + | </table> |
| | + | </div> |
| | + | |
| | + | <div class="svar"> |
| | + | <table width="100%" cellspacing="10px"> |
| | + | <tr align="left"> |
| | + | <td class="ntext">a)</td> |
| | + | <td class="ntext" width="50%">$v=\displaystyle \frac{\pi}{2}$</td> |
| | + | <td class="ntext">b)</td> |
| | + | <td class="ntext" width="50%">$v=\displaystyle \frac{3\pi}{5}$</td> |
| | + | </tr> |
| | + | <tr><td height="5px"/></tr> |
| | + | </table> |
| | + | </div> |
| | + | |
| | + | ==Övning 4.3:3== |
| | + | <div class="ovning"> |
| | + | Antag att $\,-\displaystyle \frac{\pi}{2} \leq v \leq \displaystyle \frac{\pi}{2}\,$ och att $\,\sin{v} = a\,$. Uttryck med hjälp av $\,a$ |
| | + | <table width="100%" cellspacing="10px"> |
| | + | <tr align="left"> |
| | + | <td class="ntext">a)</td> |
| | + | <td class="ntext" width="50%">$\sin{(-v)}$</td> |
| | + | <td class="ntext">b)</td> |
| | + | <td class="ntext" width="50%">$\sin{(\pi-v)}$</td> |
| | + | </tr> |
| | + | <tr align="left"> |
| | + | <td class="ntext">c)</td> |
| | + | <td class="ntext" width="50%">$\cos{v}$</td> |
| | + | <td class="ntext">d)</td> |
| | + | <td class="ntext" width="50%">$\sin{\left(\displaystyle \frac{\pi}{2}-v\right)}$</td> |
| | + | </tr> |
| | + | <tr align="left"> |
| | + | <td class="ntext">e)</td> |
| | + | <td class="ntext" width="50%">$\cos{\left( \displaystyle \frac{\pi}{2} + v\right)}$</td> |
| | + | <td class="ntext">f)</td> |
| | + | <td class="ntext" width="50%">$\sin{\left( \displaystyle \frac{\pi}{3} + v \right)}$</td> |
| | + | </tr> |
| | + | <tr><td height="5px"/></tr> |
| | + | </table> |
| | + | </div> |
| | + | |
| | + | <div class="svar"> |
| | + | <table width="100%" cellspacing="10px"> |
| | + | <tr align="left"> |
| | + | <td class="ntext">a)</td> |
| | + | <td class="ntext" width="50%">$-a$</td> |
| | + | <td class="ntext">b)</td> |
| | + | <td class="ntext" width="50%">$a$</td> |
| | + | </tr> |
| | + | <tr align="left"> |
| | + | <td class="ntext">c)</td> |
| | + | <td class="ntext" width="50%">$\sqrt{1-a^2}$</td> |
| | + | <td class="ntext">d)</td> |
| | + | <td class="ntext" width="50%">$\sqrt{1-a^2}$</td> |
| | + | </tr> |
| | + | <tr align="left"> |
| | + | <td class="ntext">e)</td> |
| | + | <td class="ntext" width="50%">$-a$</td> |
| | + | <td class="ntext">f)</td> |
| | + | <td class="ntext" width="50%">$\displaystyle \frac{\sqrt{3}}{2}\sqrt{1-a^2}+\displaystyle \frac{1}{2}\cdot a $</td> |
| | + | </tr> |
| | + | <tr><td height="5px"/></tr> |
| | + | </table> |
| | + | </div> |
| | + | |
| | + | ==Övning 4.3:4== |
| | + | <div class="ovning"> |
| | + | Antag att $\,0 \leq v \leq \pi\,$ och att $\,\cos{v}=b\,$. Uttryck med hjälp av $\,b\,$ |
| | + | <table width="100%" cellspacing="10px"> |
| | + | <tr align="left"> |
| | + | <td class="ntext">a)</td> |
| | + | <td class="ntext" width="50%">$\sin^2{v}$</td> |
| | + | <td class="ntext">b)</td> |
| | + | <td class="ntext" width="50%">$\sin{v}$</td> |
| | + | </tr> |
| | + | <tr align="left"> |
| | + | <td class="ntext">c)</td> |
| | + | <td class="ntext" width="50%">$\sin{2v}$</td> |
| | + | <td class="ntext">d)</td> |
| | + | <td class="ntext" width="50%">$\cos{2v}$</td> |
| | + | </tr> |
| | + | <tr align="left"> |
| | + | <td class="ntext">e)</td> |
| | + | <td class="ntext" width="50%">$\sin{\left( v+\displaystyle \frac{\pi}{4} \right)}$</td> |
| | + | <td class="ntext">f)</td> |
| | + | <td class="ntext" width="50%">$\cos{\left( v-\displaystyle \frac{\pi}{3} \right)}$</td> |
| | + | </tr> |
| | + | <tr><td height="5px"/></tr> |
| | + | </table> |
| | + | </div> |
| | + | |
| | + | <div class="svar"> |
| | + | <table width="100%" cellspacing="10px"> |
| | + | <tr align="left"> |
| | + | <td class="ntext">a)</td> |
| | + | <td class="ntext" width="50%">$1-b^2$</td> |
| | + | <td class="ntext">b)</td> |
| | + | <td class="ntext" width="50%">$\sqrt{1-b^2}$</td> |
| | + | </tr> |
| | + | <tr align="left"> |
| | + | <td class="ntext">c)</td> |
| | + | <td class="ntext" width="50%">$2b\sqrt{1-b^2}$</td> |
| | + | <td class="ntext">d)</td> |
| | + | <td class="ntext" width="50%">$2b^2-1$</td> |
| | + | </tr> |
| | + | <tr align="left"> |
| | + | <td class="ntext">e)</td> |
| | + | <td class="ntext" width="50%">$\sqrt{1-b^2}\cdot\displaystyle \frac{1}{\sqrt{2}} + b\cdot \displaystyle \frac{1}{\sqrt{2}} $</td> |
| | + | <td class="ntext">f)</td> |
| | + | <td class="ntext" width="50%">$b\cdot\displaystyle \frac{1}{2}+\sqrt{1-b^2}\cdot\displaystyle \frac{\sqrt{3}}{2}$</td> |
| | + | </tr> |
| | + | <tr><td height="5px"/></tr> |
| | + | </table> |
| | + | </div> |
| | + | |
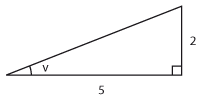
| | + | ==Övning 4.3:5== |
| | + | <div class="ovning"> |
| | + | För en spetsig vinkel $\,v\,$ i en triangel gäller att $\,\sin{v}=\displaystyle \frac{5}{7}\,$. Bestäm $\,\cos{v}\,$ och $\,\tan{v}\,$. |
| | + | </div> |
| | + | |
| | + | <div class="svar"> |
| | + | <table width="100%" cellspacing="10px"> |
| | + | <tr align="left"> |
| | + | <td class="ntext" width="100%">$\cos{v}=\displaystyle \frac{2\sqrt{6}}{7}\quad$ och $\quad\tan{v}=\displaystyle \frac{5}{2\sqrt{6}}\,$.</td> |
| | + | </tr> |
| | + | <tr><td height="5px"/></tr> |
| | + | </table> |
| | + | </div> |
| | + | |
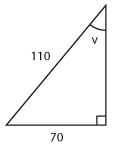
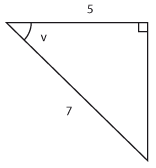
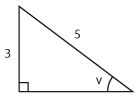
| | + | ==Övning 4.3:6== |
| | + | <div class="ovning"> |
| | + | <table width="100%" cellspacing="10px"> |
| | + | <tr align="left" valign="top"> |
| | + | <td class="ntext">a)</td> |
| | + | <td class="ntext" width="100%">Bestäm $\ \sin{v}\ $ och $\ \tan{v}\ $ om $\ \cos{v}=\displaystyle \frac{3}{4}\ $ och $\ \displaystyle \frac{3\pi}{2} \leq v \leq 2\pi\,$.</td> |
| | + | </tr> |
| | + | <tr align="left" valign="top"> |
| | + | <td class="ntext">b)</td> |
| | + | <td class="ntext" width="100%">Bestäm $\ \cos{v}\ $ och $\ \tan{v}\ $ om $\ \sin{v}=\displaystyle \frac{3}{10}\ $ och $\,v\,$ ligger i den andra kvadranten.</td> |
| | + | </tr> |
| | + | <tr align="left" valign="top"> |
| | + | <td class="ntext">c)</td> |
| | + | <td class="ntext" width="100%">Bestäm $\ \sin{v}\ $ och $\ \cos{v}\ $ om $\ \tan{v}=3\ $ och $\ \pi \leq v \leq \displaystyle \frac{3\pi}{2}\,$.</td> |
| | + | </tr> |
| | + | <tr><td height="5px"/></tr> |
| | + | </table> |
| | + | </div> |
| | + | |
| | + | <div class="svar"> |
| | + | <table width="100%" cellspacing="10px"> |
| | + | <tr align="left"> |
| | + | <td class="ntext">a)</td> |
| | + | <td class="ntext" width="100%">$\sin{v}=-\displaystyle \frac{\sqrt{7}}{4}\quad$ och $\quad\tan{v}=-\displaystyle \frac{\sqrt{7}}{3}\,$.</td> |
| | + | </tr> |
| | + | <tr><td height="5px"/></tr> |
| | + | <tr align="left"> |
| | + | <td class="ntext">b)</td> |
| | + | <td class="ntext" width="100%">$\cos{v}=-\displaystyle \frac{\sqrt{91}}{10}\quad$ och $\quad\tan{v}=-\displaystyle \frac{3}{\sqrt{91}}\,$.</td> |
| | + | </tr> |
| | + | <tr><td height="5px"/></tr> |
| | + | <tr align="left"> |
| | + | <td class="ntext">c)</td> |
| | + | <td class="ntext" width="50%">$\sin{v}=-\displaystyle \frac{3}{\sqrt{10}}\quad$ och $\quad\cos{v}=-\displaystyle \frac{1}{\sqrt{10}}\,$.</td> |
| | + | </tr> |
| | + | <tr><td height="5px"/></tr> |
| | + | </table> |
| | + | </div> |
| | + | |
| | + | ==Övning 4.3:7== |
| | + | <div class="ovning"> |
| | + | Bestäm $\ \sin{(x+y)}\ $ om |
| | + | <table width="100%" cellspacing="10px"> |
| | + | <tr align="left"> |
| | + | <td class="ntext">a)</td> |
| | + | <td class="ntext" width="100%">$\sin{x}=\displaystyle \frac{2}{3}\,$, $\ \sin{y}=\displaystyle \frac{1}{3}\ $ och $\,x\,$, $\,y\,$ är vinklar i första kvadranten.</td> |
| | + | </tr> |
| | + | <tr align="left"> |
| | + | <td class="ntext">b)</td> |
| | + | <td class="ntext" width="100%">$\cos{x}=\displaystyle \frac{2}{5}\,$, $\ \cos{y}=\displaystyle \frac{3}{5}\ $ och $\,x\,$, $\,y\,$ är vinklar i första kvadranten.</td> |
| | + | </tr> |
| | + | <tr><td height="5px"/></tr> |
| | + | </table> |
| | + | </div> |
| | + | |
| | + | <div class="svar"> |
| | + | <table width="100%" cellspacing="10px"> |
| | + | <tr align="left"> |
| | + | <td class="ntext">a)</td> |
| | + | <td class="ntext" width="100%">$\sin{(x+y)}=\displaystyle \frac{4\sqrt{2}+\sqrt{5}}{9}$</td> |
| | + | </tr> |
| | + | <tr align="left"> |
| | + | <td class="ntext">b)</td> |
| | + | <td class="ntext" width="100%">$\sin{(x+y)}=\displaystyle \frac{3\sqrt{21}+8}{25}$</td> |
| | + | </tr> |
| | + | <tr><td height="5px"/></tr> |
| | + | </table> |
| | + | </div> |
| | + | |
| | + | ==Övning 4.3:8== |
| | + | <div class="ovning"> |
| | + | Visa följande trigonometriska samband |
| | + | <table width="100%" cellspacing="10px"> |
| | + | <tr align="left"> |
| | + | <td class="ntext>a)</td> |
| | + | <td class="ntext width="100%">$\tan^2v=\displaystyle\frac{\sin^2v}{1-\sin^2v}$</td> |
| | + | </tr> |
| | + | <tr align="left"> |
| | + | <td class="ntext>b)</td> |
| | + | <td class="ntext width="100%">$\displaystyle \frac{1}{\cos v}-\tan v=\frac{\cos v}{1+\sin v}$</td> |
| | + | </tr> |
| | + | <tr align="left"> |
| | + | <td class="ntext>c)</td> |
| | + | <td class="ntext width="100%">$\tan\displaystyle\frac{u}{2}=\frac{\sin u}{1+\cos u}$</td> |
| | + | </tr> |
| | + | <tr align="left"> |
| | + | <td class="ntext>d)</td> |
| | + | <td class="ntext width="100%">$\displaystyle\frac{\cos (u+v)}{\cos u \cos v}= 1- \tan u \tan v$</td> |
| | + | </tr> |
| | + | </table> |
| | + | </div> |
| | + | |
| | + | <div class="svar"> |
| | + | <table width="100%" cellspacing="10px"> |
| | + | <tr align="left"> |
| | + | <td class="ntext">Se lösningen i webmaterialet när |
| | + | du loggat in till kursen</td> |
| | + | </tr> |
| | + | <tr><td height="5px"/></tr> |
| | + | </table> |
| | + | </div> |
| | + | |
| | + | ==Övning 4.3:9== |
| | + | <div class="ovning"> |
| | + | <table width="100%" cellspacing="10px"> |
| | + | <tr align="left"> |
| | + | <td class="ntext> |
| | + | Visa "Feynmans likhet" |
| | + | $$\cos 20^\circ \cdot \cos 40^\circ \cdot \cos 80^\circ = \displaystyle\frac{1}{8}\,\mbox{.}$$ |
| | + | (Ledtråd: Använd formeln för dubbla vinkeln på $\,\sin 160^\circ\,$.) |
| | </td> | | </td> |
| | </tr> | | </tr> |
| | </table> | | </table> |
| | </div> | | </div> |
| | + | |
| | + | <div class="svar"> |
| | + | <table width="100%" cellspacing="10px"> |
| | + | <tr align="left"> |
| | + | <td class="ntext">Se lösningen i webmaterialet när |
| | + | du loggat in till kursen</td> |
| | + | </tr> |
| | + | <tr><td height="5px"/></tr> |
| | + | </table> |
| | </div> | | </div> |
| | | | |
| - | ==Övning 4.2:9== | + | ==Övning 4.4:1== |
| | <div class="ovning"> | | <div class="ovning"> |
| - | Bilvägen från ''A'' till ''B'' består av tre rätlinjiga delar ''AP'', ''PQ'' och ''QB'', vilka är 4,0 km, 12,0 km respektive 5,0 km. De i figuren markerade vinklarna vid ''P'' och ''Q'' är 30° respektive 90°. Beräkna avståndet fågelvägen från ''A'' till ''B''. (Uppgiften är hämtad ur Centrala provet i matematik, november 1976, men aningen modifierad.) | + | För vilka vinklar $\,v\,$, där $\,0 \leq v\leq 2\pi\,$, gäller att |
| | <table width="100%" cellspacing="10px"> | | <table width="100%" cellspacing="10px"> |
| - | <tr align="center"> | + | <tr align="left"> |
| - | <td class="ntext" width="100%">[[Bild:O4_2_9.gif]]</td> | + | <td class="ntext">a)</td> |
| | + | <td class="ntext" width="50%">$\sin{v}=\displaystyle \frac{1}{2}$</td> |
| | + | <td class="ntext">b)</td> |
| | + | <td class="ntext" width="50%">$\cos{v}=\displaystyle \frac{1}{2}$</td> |
| | + | </tr> |
| | + | <tr align="left"> |
| | + | <td class="ntext">c)</td> |
| | + | <td class="ntext" width="50%">$\sin{v}=1$</td> |
| | + | <td class="ntext">d)</td> |
| | + | <td class="ntext" width="50%">$\tan{v}=1$</td> |
| | + | </tr> |
| | + | <tr align="left"> |
| | + | <td class="ntext">e)</td> |
| | + | <td class="ntext" width="50%">$\cos{v}=2$</td> |
| | + | <td class="ntext">f)</td> |
| | + | <td class="ntext" width="50%">$\sin{v}=-\displaystyle \frac{1}{2}$</td> |
| | + | </tr> |
| | + | <tr align="left"> |
| | + | <td class="ntext">g)</td> |
| | + | <td class="ntext" width="50%">$\tan{v}=-\displaystyle \frac{1}{\sqrt{3}}$</td> |
| | </tr> | | </tr> |
| | <tr><td height="5px"/></tr> | | <tr><td height="5px"/></tr> |
| Rad 736: |
Rad 934: |
| | </div> | | </div> |
| | | | |
| - | <div class=NavFrame style="CLEAR: both"> | + | <div class="svar"> |
| - | <div class=NavHead>Facit </div> | + | |
| - | <div class=NavContent> | + | |
| | <table width="100%" cellspacing="10px"> | | <table width="100%" cellspacing="10px"> |
| | <tr align="left"> | | <tr align="left"> |
| - | <td class="ntext" width="100%">Avståndet är $\ \sqrt{205-48\sqrt{3}} \approx 11{,}0$ km.</td> | + | <td class="ntext">a)</td> |
| | + | <td class="ntext" width="50%">$\displaystyle v=\frac{\pi}{6}\,$, $\,\displaystyle v=\frac{5\pi}{6}$</td> |
| | + | <td class="ntext">b)</td> |
| | + | <td class="ntext" width="50%">$\displaystyle v=\frac{\pi}{3}\,$, $\,\displaystyle v=\frac{5\pi}{3}$</td> |
| | + | </tr> |
| | + | <tr align="left"> |
| | + | <td class="ntext">c)</td> |
| | + | <td class="ntext" width="50%">$\displaystyle v=\frac{\pi}{2}$</td> |
| | + | <td class="ntext">d)</td> |
| | + | <td class="ntext" width="50%">$\displaystyle v=\frac{\pi}{4}\,$, $\,\displaystyle v=\frac{5\pi}{4}$</td> |
| | + | </tr> |
| | + | <tr align="left"> |
| | + | <td class="ntext">e)</td> |
| | + | <td class="ntext" width="50%">lösning saknas</td> |
| | + | <td class="ntext">f)</td> |
| | + | <td class="ntext" width="50%">$\displaystyle v=\frac{11\pi}{6}\,$, $\,\displaystyle v=\frac{7\pi}{6}$</td> |
| | + | </tr> |
| | + | <tr align="left"> |
| | + | <td class="ntext">g)</td> |
| | + | <td class="ntext" width="50%">$\displaystyle v=\frac{5\pi}{6}\,$, $\,\displaystyle v=\frac{11\pi}{6}$</td> |
| | </tr> | | </tr> |
| | <tr><td height="5px"/></tr> | | <tr><td height="5px"/></tr> |
| | </table> | | </table> |
| | </div> | | </div> |
| | + | |
| | + | ==Övning 4.4:2== |
| | + | <div class="ovning"> |
| | + | Lös ekvationen |
| | + | <table width="100%" cellspacing="10px"> |
| | + | <tr align="left"> |
| | + | <td class="ntext">a)</td> |
| | + | <td class="ntext" width="33%">$\sin{x}=\displaystyle \frac{\sqrt{3}}{2}$</td> |
| | + | <td class="ntext">b)</td> |
| | + | <td class="ntext" width="33%">$\cos{x}=\displaystyle \frac{1}{2} $</td> |
| | + | <td class="ntext">c)</td> |
| | + | <td class="ntext" width="33%">$\sin{x}=0$</td> |
| | + | </tr> |
| | + | <tr align="left"> |
| | + | <td class="ntext">d)</td> |
| | + | <td class="ntext" width="33%">$\sin{5x}=\displaystyle \frac{1}{\sqrt{2}} $</td> |
| | + | <td class="ntext">e)</td> |
| | + | <td class="ntext" width="33%">$\sin{5x}=\displaystyle \frac{1}{2}$</td> |
| | + | <td class="ntext">f)</td> |
| | + | <td class="ntext" width="33%">$\cos{3x}=-\displaystyle\frac{1}{\sqrt{2}}$</td> |
| | + | </tr> |
| | + | <tr><td height="5px"/></tr> |
| | + | </table> |
| | </div> | | </div> |
| | | | |
| - | <div class=NavFrame style="CLEAR: both"> | + | <div class="svar"> |
| - | <div class=NavHead>Lösning </div> | + | <table width="100%" cellspacing="10px"> |
| - | <div class=NavContent> | + | <tr align="left"> |
| - | <table width="100%"> | + | <td class="ntext">a)</td> |
| - | <tr> | + | <td class="ntext" width="33%"> |
| - | <td align="center"> | + | $\left\{\eqalign{ |
| - | [[Bild:4_2_9-1(3).gif]] | + | x&=\displaystyle\frac{\pi}{3}+2n\pi\cr |
| | + | x&=\displaystyle\frac{2\pi}{3}+2n\pi } \right.$ |
| | </td> | | </td> |
| | + | <td class="ntext">b)</td> |
| | + | <td class="ntext" width="33%"> |
| | + | $\left\{\eqalign{ |
| | + | x&=\displaystyle\frac{\pi}{3}+2n\pi\cr |
| | + | x&=\displaystyle\frac{5\pi}{3}+2n\pi } \right.$ |
| | + | </td> |
| | + | <td class="ntext">c)</td> |
| | + | <td class="ntext" width="33%"> |
| | + | $x=n\pi$</td> |
| | </tr> | | </tr> |
| - | <tr> | + | <tr align="left"> |
| - | <td align="center"> | + | <td class="ntext">d)</td> |
| - | [[Bild:4_2_9-2(3).gif]] | + | <td class="ntext" width="33%"> |
| | + | $\left\{\eqalign{ |
| | + | x&=\displaystyle\frac{\pi}{20}+\displaystyle\frac{2n\pi}{5}\cr |
| | + | x&=\displaystyle\frac{3\pi}{20}+\displaystyle\frac{2n\pi}{5} } \right.$ |
| | + | </td> |
| | + | <td class="ntext">e)</td> |
| | + | <td class="ntext" width="33%"> |
| | + | $\left\{\eqalign{ |
| | + | x&=\displaystyle\frac{\pi}{30}+\displaystyle\frac{2n\pi}{5}\cr |
| | + | x&=\displaystyle\frac{\pi}{6}+\displaystyle\frac{2n\pi}{5}} \right.$ |
| | + | </td> |
| | + | <td class="ntext">f)</td> |
| | + | <td class="ntext" width="33%"> |
| | + | $\left\{\eqalign{ |
| | + | x&=\displaystyle\frac{\pi}{4}+\displaystyle\frac{2n\pi}{3}\cr |
| | + | x&=\displaystyle\frac{5\pi}{12}+\displaystyle\frac{2n\pi}{3}} \right.$ |
| | </td> | | </td> |
| | </tr> | | </tr> |
| | + | <tr><td height="5px"/></tr> |
| | + | </table> |
| | + | </div> |
| | + | |
| | + | ==Övning 4.4:3== |
| | + | <div class="ovning"> |
| | + | Lös ekvationen |
| | + | <table width="100%" cellspacing="10px"> |
| | + | <tr align="left"> |
| | + | <td class="ntext">a)</td> |
| | + | <td class="ntext" width="50%">$\cos{x}=\cos{\displaystyle \frac{\pi}{6}}$</td> |
| | + | <td class="ntext">b)</td> |
| | + | <td class="ntext" width="50%">$\sin{x}=\sin{\displaystyle \frac{\pi}{5}}$</td> |
| | + | </tr> |
| | + | <tr align="left"> |
| | + | <td class="ntext">c)</td> |
| | + | <td class="ntext" width="50%">$\sin{(x+40^\circ)}=\sin{65^\circ}$</td> |
| | + | <td class="ntext">d)</td> |
| | + | <td class="ntext" width="50%">$\sin{3x}=\sin{15^\circ}$</td> |
| | + | </tr> |
| | + | <tr><td height="5px"/></tr> |
| | + | </table> |
| | + | </div> |
| | + | |
| | + | <div class="svar"> |
| | + | <table width="100%" cellspacing="10px"> |
| | + | <tr align="left"> |
| | + | <td class="ntext">a)</td> |
| | + | <td class="ntext" width="50%"> |
| | + | $\left\{\eqalign{ |
| | + | x&=\displaystyle\frac{\pi}{6}+2n\pi\cr |
| | + | x&=\displaystyle\frac{11\pi}{6}+2n\pi |
| | + | }\right.$ |
| | + | </td> |
| | + | <td class="ntext">b)</td> |
| | + | <td class="ntext" width="50%"> |
| | + | $\left\{\eqalign{ |
| | + | x&=\displaystyle\frac{\pi}{5}+2n\pi\cr |
| | + | x&=\displaystyle\frac{4\pi}{5}+2n\pi |
| | + | }\right.$ |
| | + | </td> |
| | + | </tr> |
| | + | <tr align="left"> |
| | + | <td class="ntext">c)</td> |
| | + | <td class="ntext" width="50%"> |
| | + | $\left\{\eqalign{ |
| | + | x&=25^\circ + n\cdot 360^\circ\cr |
| | + | x&=75^\circ + n\cdot 360^\circ |
| | + | }\right.$ |
| | + | </td> |
| | + | <td class="ntext">d)</td> |
| | + | <td class="ntext" width="50%"> |
| | + | $\left\{\eqalign{ |
| | + | x&=5^\circ + n \cdot 120^\circ \cr |
| | + | x&= 55^\circ + n \cdot 120^\circ |
| | + | }\right.$ |
| | + | </td> |
| | + | </tr> |
| | + | <tr><td height="5px"/></tr> |
| | + | </table> |
| | + | </div> |
| | + | |
| | + | ==Övning 4.4:4== |
| | + | <div class="ovning"> |
| | + | Bestäm de vinklar $\,v\,$ i intervallet $\,0^\circ \leq v \leq 360^\circ\,$ som uppfyller $\ \cos{\left(2v+10^\circ\right)}=\cos{110^\circ}\,$. |
| | + | </div> |
| | + | |
| | + | <div class="svar"> |
| | + | <table width="100%" cellpadding="10px"> |
| | <tr> | | <tr> |
| - | <td align="center"> | + | <td align="left"> |
| - | [[Bild:4_2_9-3(3).gif]] | + | $v_1=50^\circ$, $\ \ v_2=120^\circ$, $\ \ v_3=230^\circ\ \ $ och $\ \ v_4=300^\circ$ |
| | </td> | | </td> |
| | </tr> | | </tr> |
| | </table> | | </table> |
| | </div> | | </div> |
| | + | |
| | + | ==Övning 4.4:5== |
| | + | <div class="ovning"> |
| | + | Lös ekvationen |
| | + | <table width="100%" cellspacing="10px"> |
| | + | <tr align="left"> |
| | + | <td class="ntext">a)</td> |
| | + | <td class="ntext" width="50%">$\sin{3x}=\sin{x}$</td> |
| | + | <td class="ntext">b)</td> |
| | + | <td class="ntext" width="50%">$\tan{x}=\tan{4x}$</td> |
| | + | </tr> |
| | + | <tr align="left"> |
| | + | <td class="ntext">c)</td> |
| | + | <td class="ntext" width="50%">$\cos{5x}=\cos(x+\pi/5)$</td> |
| | + | </tr> |
| | + | <tr><td height="5px"/></tr> |
| | + | </table> |
| | + | </div> |
| | + | |
| | + | <div class="svar"> |
| | + | <table width="100%" cellspacing="10px"> |
| | + | <tr align="left"> |
| | + | <td class="ntext">a)</td> |
| | + | <td class="ntext" width="50%"> |
| | + | $\left\{\eqalign{ |
| | + | x&=n\pi\cr |
| | + | x&=\displaystyle \frac{\pi}{4}+\displaystyle \frac{n\pi}{2} |
| | + | }\right.$ |
| | + | </td> |
| | + | <td class="ntext">b)</td> |
| | + | <td class="ntext" width="50%">$x=\displaystyle \frac{n\pi}{3}$</td> |
| | + | </tr> |
| | + | <tr align="left"> |
| | + | <td class="ntext">c)</td> |
| | + | <td class="ntext" width="50%"> |
| | + | $\left\{\eqalign{ |
| | + | x&=\displaystyle \frac{\pi}{20}+\displaystyle \frac{n\pi}{2}\cr |
| | + | x&=-\displaystyle \frac{\pi}{30}+\displaystyle \frac{n\pi}{3} |
| | + | }\right.$ |
| | + | </td> |
| | + | </tr> |
| | + | <tr><td height="5px"/></tr> |
| | + | </table> |
| | + | </div> |
| | + | |
| | + | ==Övning 4.4:6== |
| | + | <div class="ovning"> |
| | + | Lös ekvationen |
| | + | <table width="100%" cellspacing="10px"> |
| | + | <tr align="left"> |
| | + | <td class="ntext">a)</td> |
| | + | <td class="ntext" width="50%">$\sin x\cdot \cos 3x = 2\sin x$</td> |
| | + | <td class="ntext">b)</td> |
| | + | <td class="ntext" width="50%">$\sqrt{2}\sin{x}\cos{x}=\cos{x}$</td> |
| | + | </tr> |
| | + | <tr align="left"> |
| | + | <td class="ntext">c)</td> |
| | + | <td class="ntext" width="50%">$\sin 2x = -\sin x$</td> |
| | + | </tr> |
| | + | <tr><td height="5px"/></tr> |
| | + | </table> |
| | + | </div> |
| | + | |
| | + | <div class="svar"> |
| | + | <table width="100%" cellspacing="10px"> |
| | + | <tr align="left"> |
| | + | <td class="ntext">a)</td> |
| | + | <td class="ntext" width="50%"> |
| | + | $x=n\pi$ |
| | + | </td> |
| | + | <td class="ntext">b)</td> |
| | + | <td class="ntext" width="50%"> |
| | + | $\left\{\eqalign{ |
| | + | x&=\displaystyle \frac{\pi}{4}+2n\pi\cr |
| | + | x&=\displaystyle \frac{\pi}{2}+n\pi\cr |
| | + | x&=\displaystyle \frac{3\pi}{4}+2n\pi}\right.$ |
| | + | </td> |
| | + | </tr> |
| | + | <tr align="left"> |
| | + | <td class="ntext">c)</td> |
| | + | <td class="ntext" width="50%"> |
| | + | $\left\{\eqalign{ |
| | + | x&=\displaystyle \frac{2n\pi}{3}\cr |
| | + | x&=\displaystyle \pi + 2n\pi\cr |
| | + | }\right.$ |
| | + | </td> |
| | + | </tr> |
| | + | <tr><td height="5px"/></tr> |
| | + | </table> |
| | + | </div> |
| | + | |
| | + | ==Övning 4.4:7== |
| | + | <div class="ovning"> |
| | + | Lös ekvationen |
| | + | <table width="100%" cellspacing="10px"> |
| | + | <tr align="left"> |
| | + | <td class="ntext">a)</td> |
| | + | <td class="ntext" width="50%">$2\sin^2{x}+\sin{x}=1$</td> |
| | + | <td class="ntext">b)</td> |
| | + | <td class="ntext" width="50%">$2\sin^2{x}-3\cos{x}=0$</td> |
| | + | </tr> |
| | + | <tr align="left"> |
| | + | <td class="ntext">c)</td> |
| | + | <td class="ntext" width="50%">$\cos{3x}=\sin{4x}$</td> |
| | + | </tr> |
| | + | <tr><td height="5px"/></tr> |
| | + | </table> |
| | + | </div> |
| | + | |
| | + | <div class="svar"> |
| | + | <table width="100%" cellspacing="10px"> |
| | + | <tr align="left"> |
| | + | <td class="ntext">a)</td> |
| | + | <td class="ntext" width="50%"> |
| | + | $\left\{ \matrix{ |
| | + | x=\displaystyle \frac{\pi}{6}+2n\pi\cr |
| | + | x=\displaystyle \frac{5\pi}{6}+2n\pi\cr |
| | + | x=\displaystyle \frac{3\pi}{2}+2n\pi |
| | + | }\right.$ |
| | + | </td> |
| | + | <td class="ntext">b)</td> |
| | + | <td class="ntext" width="50%">$x=\pm \displaystyle \frac{\pi}{3} + 2n\pi $</td> |
| | + | </tr> |
| | + | <tr align="left"> |
| | + | <td class="ntext">c)</td> |
| | + | <td class="ntext" width="50%"> |
| | + | $\left\{ \matrix{ |
| | + | x=\displaystyle \frac{\pi}{2}+2n\pi\cr |
| | + | x=\displaystyle \frac{\pi}{14}+\displaystyle \frac{2n\pi}{7} |
| | + | }\right.$ |
| | + | </td> |
| | + | </tr> |
| | + | <tr><td height="5px"/></tr> |
| | + | </table> |
| | + | </div> |
| | + | |
| | + | ==Övning 4.4:8== |
| | + | <div class="ovning"> |
| | + | Lös ekvationen |
| | + | <table width="100%" cellspacing="10px"> |
| | + | <tr align="left"> |
| | + | <td class="ntext">a)</td> |
| | + | <td class="ntext" width="50%">$\sin{2x}=\sqrt{2}\cos{x}$</td> |
| | + | <td class="ntext">b)</td> |
| | + | <td class="ntext" width="50%">$\sin{x}=\sqrt{3}\cos{x}$</td> |
| | + | </tr> |
| | + | <tr align="left"> |
| | + | <td class="ntext">c)</td> |
| | + | <td class="ntext" width="50%">$\displaystyle \frac{1}{\cos^2{x}}=1-\tan{x}$</td> |
| | + | </tr> |
| | + | <tr><td height="5px"/></tr> |
| | + | </table> |
| | + | </div> |
| | + | |
| | + | <div class="svar"> |
| | + | <table width="100%" cellspacing="10px"> |
| | + | <tr align="left"> |
| | + | <td class="ntext">a)</td> |
| | + | <td class="ntext" width="50%"> |
| | + | $\left\{\eqalign{ |
| | + | x&=\displaystyle \frac{\pi}{4}+2n\pi\cr |
| | + | x&=\displaystyle \frac{\pi}{2}+n\pi\cr |
| | + | x&=\displaystyle \frac{3\pi}{4}+2n\pi |
| | + | }\right.$ |
| | + | </td> |
| | + | <td class="ntext">b)</td> |
| | + | <td class="ntext" width="50%">$x=\displaystyle \frac{\pi}{3}+n\pi$</td> |
| | + | </tr> |
| | + | <tr align="left"> |
| | + | <td class="ntext">c)</td> |
| | + | <td class="ntext" width="50%"> |
| | + | $\left\{\eqalign{ |
| | + | x&=n\pi\cr |
| | + | x&=\displaystyle \frac{3\pi}{4}+n\pi |
| | + | }\right.$ |
| | + | </td> |
| | + | </tr> |
| | + | <tr><td height="5px"/></tr> |
| | + | </table> |
| | </div> | | </div> |