Teori
Andragradsekvationer
En andragradsekvation är en ekvation som kan skrivas som
$$x^2+px+q=0$$
där $x$ är den obekanta och $p$ och $q$ är konstanter.
Enklare typer av andragradsekvationer kan vi lösa direkt genom rotutdragning.
Ekvationen $\,x^2=a\,$ där $a$ är ett postivt tal har två lösningar (rötter) $\,x=\sqrt{a}\,$ och $\,x=-\sqrt{a}\,$.
Exempel 1
- $x^2 = 4 \quad$ har rötterna $\,x=\sqrt{4} = 2\,$ och $\,x=-\sqrt{4}= -2\,$.
- $2x^2=18 \quad$ skrivs om till $\,x^2=9\,$ och har rötterna $\,x=\sqrt9 = 3\,$ och $\,x=-\sqrt9 = -3\,$.
- $3x^2-15=0 \quad$ kan skrivas som $\,x^2=5\,$ och har rötterna $\,x=\sqrt5 \approx 2{,}236\,$ och $\,x=-\sqrt5 \approx -2{,}236\,$.
- $9x^2+25=0\quad$ saknar lösningar eftersom vänsterledet kommer alltid att vara större än eller lika med 25 oavsett hur $x$ väljs (kvadraten $x^2$ är alltid större än eller lika med noll).
Exempel 2
- Lös ekvationen $\ (x-1)^2 = 16\,$.
Genom att betrakta $\,x-1\,$ som obekant ger rotutdragning att ekvationen har två lösningar:
- $x-1 =\sqrt{16} = 4\,$ vilket ger att $\,x=1+4=5\,$,
- $x-1 = -\sqrt{16} = -4\,$ vilket ger att $\,x=1-4=-3\,$.
- Lös ekvationen $\ 2(x+1)^2 -8=0\,$.
Flytta över termen $8$ till högerledet och dela båda led med $2$,
$$(x+1)^2=4 \; \mbox{.}$$
Rotutdragning ger att:
- $x+1 =\sqrt{4} = 2, \quad \mbox{d.v.s.} \quad x=-1+2=1$
- $x+1 = -\sqrt{4} = -2, \quad \mbox{d.v.s.} \quad x=-1-2=-3$
För att lösa allmänna andragradsekvationer använder vi en teknik som kallas kvadratkomplettering.
Om vi betraktar kvadreringsregeln
$$x^2 + 2ax + a^2 = (x+a)^2$$
och subtraherar $a^2$ från båda led så får vi
Kvadratkomplettering:
$$x^2 +2ax = (x+a)^2 -a^2$$
Exempel 3
- Lös ekvationen $\ x^2 +2x -8=0\,$.
De två termerna $\,x^2+2x\,$ kvadratkompletteras (använd $\,a=1\,$ i formeln)
$$\underline{\vphantom{(}x^2+2x} -8 = \underline{(x+1)^2-1^2} -8 = (x+1)^2-9,$$
där understrykningen visar vilka termer som är inblandade i kvadratkompletteringen. Ekvationen kan därför skrivas som
$$(x+1)^2 -9 = 0,$$
vilken vi löser med rotutdragning
- $x+1 =\sqrt{9} = 3\,$ och därmed $\,x=-1+3=2\,$,
- $x+1 =-\sqrt{9} = -3\,$ och därmed $\,x=-1-3=-4\,$.
- Lös ekvationen $\ 2x^2 -2x - \frac{3}{2} = 0\,$.
Dividera båda led med 2
$$x^2-x-\textstyle\frac{3}{4}=0\mbox{.}$$
Vänsterledet kvadratkompletteras (använd $a=-\frac{1}{2}$)
$$\textstyle\underline{\vphantom{\bigl(\frac{3}{4}}x^2-x} -\frac{3}{4} = \underline{\bigl(x-\frac{1}{2}\bigr)^2 - \bigl(-\frac{1}{2}\bigr)^2} -\frac{3}{4}= \bigl(x-\frac{1}{2}\bigr)^2 -1$$
och detta ger oss ekvationen
$$\textstyle\bigl(x-\frac{1}{2}\bigr)^2 - 1=0\,\mbox{.}$$
Rotutdragning ger att
- $x-\frac{1}{2} =\sqrt{1} = 1, \quad$ d.v.s. $\quad x=\frac{1}{2}+1=\frac{3}{2}\,$,
- $x-\frac{1}{2}= -\sqrt{1} = -1, \quad$ d.v.s. $\quad x=\frac{1}{2}-1= -\frac{1}{2}\,$.
Tips:
Tänk på att man alltid kan pröva lösningar till en ekvation genom att sätta in värdet och se om ekvationen blir uppfylld. Man gör detta för att upptäcka eventuella slarvfel. För exempel 3a ovan har vi två fall att pröva. Vi kallar vänster- och högerleden för VL respektive HL:
- $x = 2\,$ medför att $\,\mbox{VL} = 2^2 +2\cdot 2 - 8 = 4+4-8 = 0 = \mbox{HL}\,$.
- $x = -4$ medför att $\,\mbox{VL} = (-4)^2 + 2\cdot(-4) -8 = 16-8-8 = 0 = \mbox{HL}\,$.
I båda fallen kommer vi fram till VL = HL. Ekvationen är alltså uppfylld i båda fallen.
Med kvadratkomplettering går det att visa att den allmänna andragradsekvationen
$$x^2+px+q=0$$
har lösningarna
$$x = - \displaystyle\frac{p}{2} \pm \sqrt{\left(\frac{p}{2}\right)^2-q}$$
förutsatt att uttrycket under rottecknet inte är negativt.
Ibland kan man faktorisera ekvationer och direkt se vilka lösningarna är.
Exempel 4
- Lös ekvationen $\ x^2-4x=0\,$.
I vänsterledet kan vi bryta ut ett $x$
- $x(x-4)=0\,$.
Ekvationens vänsterled blir noll när någon av faktorerna är noll, vilket ger oss två lösningar
- $x =0,\quad$ eller
- $x-4=0\quad$ d.v.s. $\quad x=4\,$.
Parabler
Funktionerna
$$\eqalign{y&=x^2-2x+5\cr y&=4-3x^2\cr y&=\textstyle\frac{1}{5}x^2 +3x}$$
är exempel på andragradsfunktioner. Allmänt kan en andragradsfunktion skrivas som
$$y=ax^2+bx+c$$
där $a$, $b$ och $c$ är konstanter och där $a\ne0$.
Grafen till en andragradsfunktion kallas för en parabel och figurerna visar utseendet för två typexempel $\,y=x^2\,$ och $\,y=-x^2$.
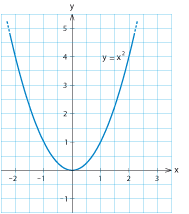 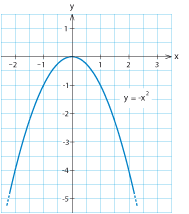
Eftersom uttrycket $\,x^2\,$ är som minst när $\,x=0\,$ har parabeln $\,y=x^2\,$ ett minimum när $\,x=0\,$ och parabeln $\,y=-x^2\,$ ett maximum för $\,x=0\,$.
Notera också att parablerna ovan är symmetriska kring $y$-axeln eftersom värdet på $\,x^2\,$ inte beror på vilket tecken $x$ har.
Exempel 5
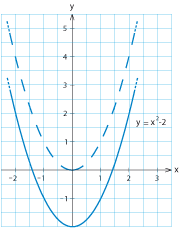
- Skissera parabeln $\ y=x^2-2\,$.
Jämfört med parabeln $\,y=x^2\,$ har punkter på parabeln ($\,y=x^2-2\,$) $y$-värden som är två enheter mindre, d.v.s. parabeln är förskjuten två enheter neråt i $y$-led.
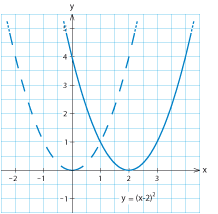
- Skissera parabeln $\ y=(x-2)^2\,$.
På parabeln $\,y=(x-2)^2\,$ behöver vi välja $x$-värden två enheter större jämfört med parabeln $\,y=x^2\,$ för att få motsvarande $y$-värden. Alltså är parabeln $\,y=(x-2)^2\,$ förskjuten två enheter åt höger jämfört med $\,y=x^2\,$.
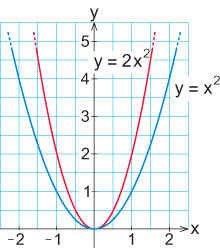
- Skissera parabeln $\,y=2x^2\,$.
Varje punkt på parabeln $\,y=2x^2\,$ har dubbelt så stort $y$-värde än vad motsvarande punkt med samma $x$-värde har på parabeln $\,y=x^2\,$. Parabeln $\,y=2x^2\,$ är expanderad med faktorn $2$ i $y$-led jämfört med $\,y=x^2\,$.
Med kvadratkomplettering kan vi behandla alla typer av parabler.
Exempel 6
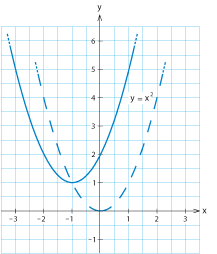
Skissera parabeln $\ y=x^2+2x+2\,$.
Om högerledet kvadratkompletteras
$x^2 +2x+2 = (x+1)^2 -1^2 +2 = (x+1)^2+1$
så ser vi från det resulterande uttrycket $\,y= (x+1)^2+1\,$ att parabeln är förskjuten en enhet åt vänster i $x$-led jämfört med $\,y=x^2\,$ (eftersom det står $\,(x+1)^2\,$ istället för $\,x^2\,$) och en enhet uppåt i $y$-led.
</td>
|
 |
</tr>
</table>
Exempel 7
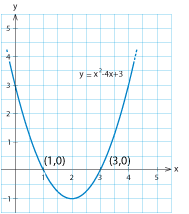
Bestäm var parabeln $\,y=x^2-4x+3\,$ skär $x$-axeln.
En punkt ligger på $x$-axeln om dess $y$-koordinat är noll, och de punkter på parabeln som har $y=0$ har en $x$-koordinat som uppfyller ekvationen
$x^2-4x+3=0\mbox{.}$
<table
Vänsterledet kvadratkompletteras
$$x^2-4x+3=(x-2)^2-2^2+3=(x-2)^2-1$$
och detta ger ekvationen
$$(x-2)^2= 1 \; \mbox{.}$$
Efter rotutdragning får vi lösningarna
- $x-2 =\sqrt{1} = 1,\quad$ d.v.s. $\quad x=2+1=3\,$,
- $x-2 = -\sqrt{1} = -1,\quad$ d.v.s. $\quad x=2-1=1\,$.
Parabeln skär $x$-axeln i punkterna $\,(1,0)\,$ och $\,(3,0)\,$.
Exempel 8
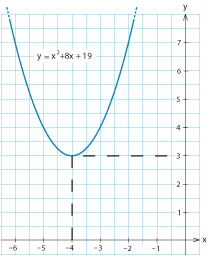
Bestäm det minsta värde som uttrycket $\,x^2+8x+19\,$ antar.
Vi kvadratkompletterar
$x^2 +8x+19=(x+4)^2 -4^2 +19 = (x+4)^2 +3$
och då ser vi att uttrycket blir som minst lika med 3 eftersom kvadraten $\,(x+4)^2\,$ alltid är större än eller lika med 0 oavsett vad $x$ är.
I figuren till höger ser vi att hela parabeln $\,y=x^2+8x+19\,$ ligger ovanför $x$-axeln och har ett minimumvärde 3 när $\,x=-4\,$.
Tänk på att:
Lägg ner mycket tid på algebra! Algebra är matematikens alfabet. När du väl har förstått algebra, kommer din förståelse av statistik, yta, volym och geometri vara mycket större.
|