4. Trigonometri
Sommarmatte 1
| Versionen från 10 maj 2007 kl. 15.48 (redigera) Lina (Diskussion | bidrag) ← Gå till föregående ändring |
Nuvarande version (12 januari 2008 kl. 11.06) (redigera) (ogör) KTH.SE:u1m1gion (Diskussion | bidrag) m (→Vad är geometri?) |
||
| (16 mellanliggande versioner visas inte.) | |||
| Rad 1: | Rad 1: | ||
| - | =Geometri och trigonometri - inledning= | + | __NOTOC__ |
| - | + | <table><tr><td width="600"> | |
| + | {|align="left" | ||
| + | |[[Bild:772696.jpg|left]] | ||
| + | |} | ||
| '''Hur gammal är geometrin och trigonometrin egentligen och när började man använda dessa metoder för att lösa problem?''' | '''Hur gammal är geometrin och trigonometrin egentligen och när började man använda dessa metoder för att lösa problem?''' | ||
| - | <i>''Titta på videon där universitetslektor Lasse Svensson berättar om hur geometri och trigonometri utvecklats och svarar på Elins frågor.''</i> | + | |
| + | ''Titta på videon där universitetslektor Lasse Svensson berättar om hur geometri och trigonometri utvecklats och svarar på Elins frågor.'' | ||
| + | |||
| [http://smaug.nti.se/temp/KTH/film5.html Starta videon Introduktion till Geometrin] | [http://smaug.nti.se/temp/KTH/film5.html Starta videon Introduktion till Geometrin] | ||
| Rad 13: | Rad 18: | ||
| Den kanske mest berömde är '''EUKLIDES''' (300-talet f.Kr). Han gav ut ett berömt verk med titeln '''ELEMENTA''' - där han sammanfattade sin tids matematiska vetande. På 1600-talet började man ifrågasätta en del av Euklides s.k '''AXIOM''' och det utvecklades en '''ICKE-EUKLIDISK''' geometri som fick stor betydelse i olika sammanhang. | Den kanske mest berömde är '''EUKLIDES''' (300-talet f.Kr). Han gav ut ett berömt verk med titeln '''ELEMENTA''' - där han sammanfattade sin tids matematiska vetande. På 1600-talet började man ifrågasätta en del av Euklides s.k '''AXIOM''' och det utvecklades en '''ICKE-EUKLIDISK''' geometri som fick stor betydelse i olika sammanhang. | ||
| + | |||
| Trigonometri betyder "triangelmätning" och är en metod för att beräkna vinklar och sidor i rätvinkliga trianglar. Trigonometrin utvecklades några hundra år före Kristi födelse. En av de mest kända matematikerna då var HIPPARKUS, som arbetade med cirkeln och kordor i cirkeln. För varje korda kunde han beräkna motsvarande cirkelbåges längd och på så sätt kunde han bestämma sidor och vinklar i trianglar. Detta hände 2200 år före miniräknarens tillkomst! | Trigonometri betyder "triangelmätning" och är en metod för att beräkna vinklar och sidor i rätvinkliga trianglar. Trigonometrin utvecklades några hundra år före Kristi födelse. En av de mest kända matematikerna då var HIPPARKUS, som arbetade med cirkeln och kordor i cirkeln. För varje korda kunde han beräkna motsvarande cirkelbåges längd och på så sätt kunde han bestämma sidor och vinklar i trianglar. Detta hände 2200 år före miniräknarens tillkomst! | ||
| + | |||
| I detta kapitel ska vi se några exempel på hur geometriska objekt som linjer, parabler och cirklar beskrivs av ekvationer. På liknande sätt kan olika områden beskrivas av olikheter. | I detta kapitel ska vi se några exempel på hur geometriska objekt som linjer, parabler och cirklar beskrivs av ekvationer. På liknande sätt kan olika områden beskrivas av olikheter. | ||
| + | |||
| Rad 29: | Rad 37: | ||
| Om man är van att tänka på cosinus och sinus som förhållanden mellan sidorna i en rätvinklig triangel så är det viktigt att också fundera ordentligt på dessa funktioner i enhetscirkeln. Denna bild gör det lättare att förstå trigonometriska samband som periodicitet, trigonometriska ettan, samband för dubblering av vinkeln samt formler för derivator. | Om man är van att tänka på cosinus och sinus som förhållanden mellan sidorna i en rätvinklig triangel så är det viktigt att också fundera ordentligt på dessa funktioner i enhetscirkeln. Denna bild gör det lättare att förstå trigonometriska samband som periodicitet, trigonometriska ettan, samband för dubblering av vinkeln samt formler för derivator. | ||
| + | |||
| + | [[Bild:762330.jpg|right]] | ||
| Att hantera och manipulera med trigonometriska uttryck är viktigt inom de flesta tillämpningar av matematiken. De avslutande avsnitten ger en grundlig övning på detta. | Att hantera och manipulera med trigonometriska uttryck är viktigt inom de flesta tillämpningar av matematiken. De avslutande avsnitten ger en grundlig övning på detta. | ||
| Rad 36: | Rad 46: | ||
| - | '''Observera att materialet i denna kursdel---liksom i övriga delar av kursen---är utformat för att man ska arbeta med det utan hjälp av miniräknare.''' | + | '''Observera att materialet i denna kursdel – liksom i övriga delar av kursen – är utformat för att man ska arbeta med det utan hjälp av miniräknare.''' |
| - | [http://www.theducation.se/kurser/experiment/gyma/applets/ex31_randvinkelsatsen/index.html Experimentera med randvinkelsatsen] | ||
| - | + | <div class="inforuta"> | |
| - | {| BORDER="1" CELLPADDING="5" CELLSPACING="0" ALIGN="center" | + | '''Så här lyckas du med Trigonometri''' |
| - | |- | + | |
| - | | '''Så här lyckas du med Geometrin, inlämningsuppgift och gruppövning''' | + | |
| # Börja med att läsa genomgången till ett avsnitt och tänka igenom exemplen. | # Börja med att läsa genomgången till ett avsnitt och tänka igenom exemplen. | ||
| Rad 51: | Rad 58: | ||
| # Skulle du fastna, se efter om någon ställt en fråga om just detta i avsnittets forum. Ställ annars en fråga om du undrar över något. Din lärare (eller en studiekamrat) kommer att besvara den inom några timmar. | # Skulle du fastna, se efter om någon ställt en fråga om just detta i avsnittets forum. Ställ annars en fråga om du undrar över något. Din lärare (eller en studiekamrat) kommer att besvara den inom några timmar. | ||
| # När du är klar med övningsuppgifterna och grundproven i ett avsnitt så ska du göra slutprovet för att bli godkänd på avsnittet. Där gäller det att svara rätt på tre frågor i följd för att kunna gå vidare. | # När du är klar med övningsuppgifterna och grundproven i ett avsnitt så ska du göra slutprovet för att bli godkänd på avsnittet. Där gäller det att svara rätt på tre frågor i följd för att kunna gå vidare. | ||
| - | # När du fått alla rätt på både grundprov och slutprov, så ska du gå vidare och arbeta med en inlämningsuppgift. I menyraden till vänster finns ett exempel på hur en sådan inlämninguppgift kan se ut. Din egen inlämningsuppgift slumpas fram bland ett antal olika uppgifter och kommer att visas i menyraden, så fort du har blivit godkänd på alla grundprov och slutprov i kursen. | + | # När du fått alla rätt på både grundprov och slutprov, så ska du gå vidare till Del 5 och arbeta med en inlämnings- och gruppuppgiften. Länk till dessa hittar du i "Student Lounge". |
| - | # När du skickat in din inlämningsuppgift kommer du automatiskt att bli grupperad med tre andra studenter i kursen som nyligen har skickat in sin inlämningsuppgift och ni får tillsammans ett grupprum. Där kan ni se varandras inlämningsuppgifter och ni får dessutom tillgång till ett eget diskussionsforum. | + | |
| - | #Gruppuppgiften går ut på att diskutera varandras lösningar på de olika uppgifterna och tillsammans komma fram till en "bästa" förbättrad lösning på samtliga uppgifter. Det är dessa "bästa" lösningar som utgör er gruppinlämning, tillsammans med en redogörelse för hur var och en har jobbat för att komma fram till lösningarna.Här är målet att man i gruppen ska diskutera matematik, ställa frågor på sådant man tycker är oklart i de olika lösningarna, förklara hur man själv har tänkt, svara på inlägg från de övriga gruppdeltagarna och hjälpa till att sammanställa. När gruppen är nöjd så lämnar ni in er gruppinlämning, som blir bedömd och kommenterad av examinatorn. Examinatorn kommunicerar med hela gruppen, och om det är något gruppen har missat så har man möjlighet göra nya gruppinlämningar tills allt är klart och godkänt. För att bli godkänd på gruppuppgiften måste du delta aktivt, t.ex. genom att ställa frågor och hjälpa till att arbeta fram förslag på gruppinlämning. Den individuella inlämningen behöver inte vara perfekt, utan det är i gruppen som de slutliga lösningarna färdigställs. Kör ni fast, eller blir osäkra på något, kan ni alltid ställa frågor till lärarna och få vägledning. Vårt mål är att alla ska klara allting i den här kursen - och att ni ska känna att ni kommer riktigt väl förberedda till era högskolestudier. <br> | + | |
| - | Du får mer information om hur allt detta går till när du kommer hit i kursen. | + | |
| - | + | ||
| PS. Tycker du att innehållet i ett avsnitt känns väldigt bekant, så kan du testa att gå direkt till grundprovet och slutprovet. Du måste få alla rätt på ett prov, men kan göra om proven flera gånger, om du inte lyckas på första försöket. Det är ditt senaste resultat som visas i statistiken. | PS. Tycker du att innehållet i ett avsnitt känns väldigt bekant, så kan du testa att gå direkt till grundprovet och slutprovet. Du måste få alla rätt på ett prov, men kan göra om proven flera gånger, om du inte lyckas på första försöket. Det är ditt senaste resultat som visas i statistiken. | ||
| |} | |} | ||
| - | © Copyright 2006, KTH Matematik | + | </div> |
| + | |||
| + | |||
| + | <!-- slut teori --> | ||
| + | <!--ej wiki</div></td>--> | ||
| + | <td valign="top"> | ||
| + | |||
| + | <!-- rätt/fel in här --> | ||
| + | |||
| + | </td><!--ej i wiki</tr></table>--> | ||
Nuvarande version
Hur gammal är geometrin och trigonometrin egentligen och när började man använda dessa metoder för att lösa problem?
[redigera] Vad är geometri?Geometri är en mycket gammal vetenskap. Geometri är grekiska och betyder ”läran om rummet”. "Ge" står för jord och "metrein" betyder mäta. Långt före Jesu födelse hade skickliga matematiker utvecklat geometrin. Den kanske mest berömde är EUKLIDES (300-talet f.Kr). Han gav ut ett berömt verk med titeln ELEMENTA - där han sammanfattade sin tids matematiska vetande. På 1600-talet började man ifrågasätta en del av Euklides s.k AXIOM och det utvecklades en ICKE-EUKLIDISK geometri som fick stor betydelse i olika sammanhang.
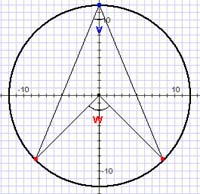
Enhetscirkeln är särskilt viktig Cirkeln med radie 1 runt origo är speciellt viktig. I denna cirkel kan man sammanfatta olika vinkelbegrepp samt de trigonometriska funktionerna cosinus och sinus. En vinkel ges av en punkt på enhetscirkeln, dess vinkelmått är sträckan längs cirkeln till punkten (1,0), cosinus för vinkeln är punktens x-komponent, sinus för vinkeln är y-komponenten av punkten. Funktionerna cosinus och sinus används alltså för att översätta från vinklar till sträckor. Om man är van att tänka på cosinus och sinus som förhållanden mellan sidorna i en rätvinklig triangel så är det viktigt att också fundera ordentligt på dessa funktioner i enhetscirkeln. Denna bild gör det lättare att förstå trigonometriska samband som periodicitet, trigonometriska ettan, samband för dubblering av vinkeln samt formler för derivator.
Att hantera och manipulera med trigonometriska uttryck är viktigt inom de flesta tillämpningar av matematiken. De avslutande avsnitten ger en grundlig övning på detta. Tidigare räknades geometrin till de viktigare momenenten inom matematikundervisningen. Under de senaste decennierna har geometrin minskats ner i såväl gymnasiets som i högskolans kurser. Men, för den som kommer att syssla med bilder eller grafik eller med konstruktioner och design (t ex CAD), så är goda kunskaper i geometri mycket värdefulla. Kunskaper i geometri är också väldigt bra att ha med sig ut i vardagslivet, där man ofta ställs inför geometriska problem och funderingar.
Så här lyckas du med Trigonometri
PS. Tycker du att innehållet i ett avsnitt känns väldigt bekant, så kan du testa att gå direkt till grundprovet och slutprovet. Du måste få alla rätt på ett prov, men kan göra om proven flera gånger, om du inte lyckas på första försöket. Det är ditt senaste resultat som visas i statistiken. |}
|
|