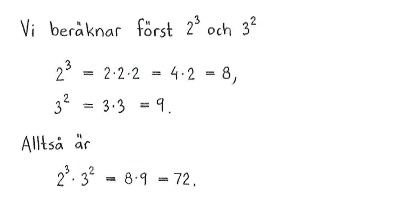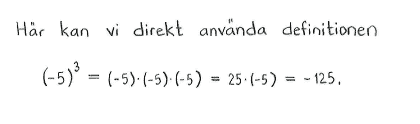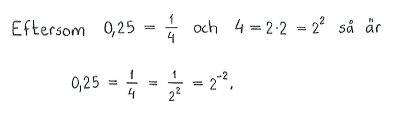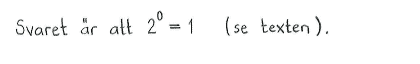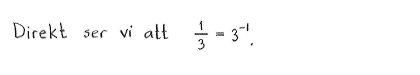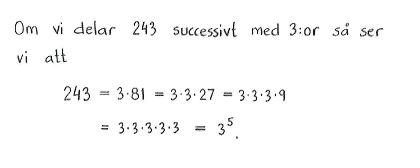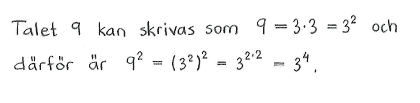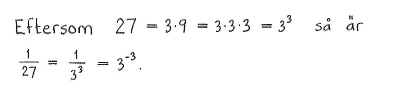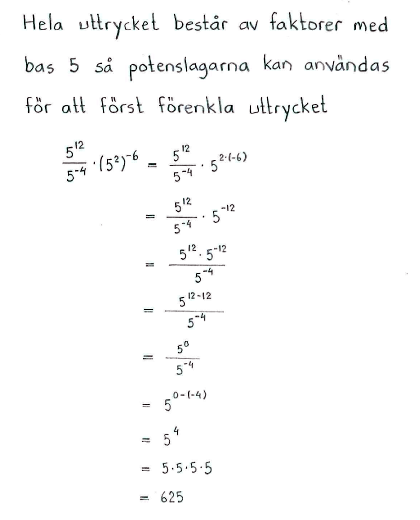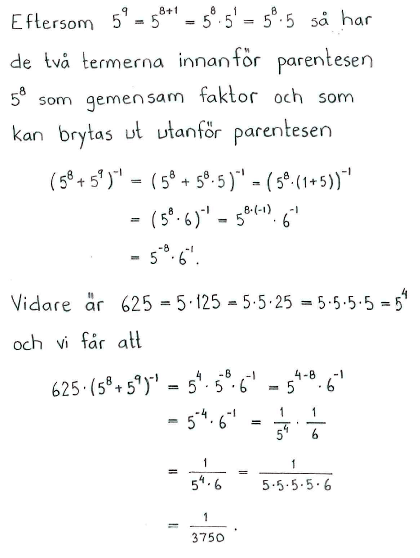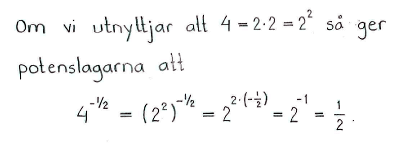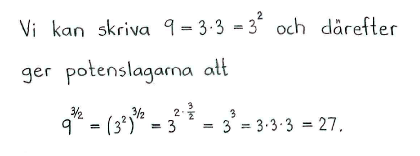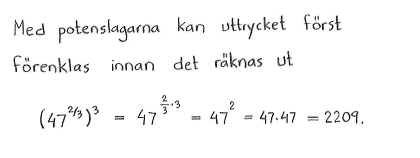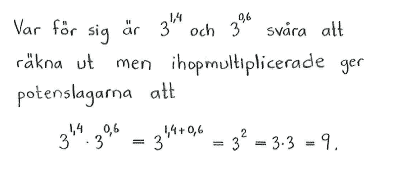1.3 Övningar
Sommarmatte 1
| Versionen från 12 maj 2007 kl. 17.17 (redigera) Tek (Diskussion | bidrag) (En del ändringar) ← Gå till föregående ändring |
Nuvarande version (25 maj 2007 kl. 11.14) (redigera) (ogör) KTH.SE:u1qh5fat (Diskussion | bidrag) (→Övning 1.3:4) |
||
| (En mellanliggande version visas inte.) | |||
| Rad 1: | Rad 1: | ||
| - | __NOTOC__ | ||
| ==Övning 1.3:1== | ==Övning 1.3:1== | ||
| Rad 294: | Rad 293: | ||
| <td class="ntext" width="33%">$2^{9}\cdot2^{-7}$</td> | <td class="ntext" width="33%">$2^{9}\cdot2^{-7}$</td> | ||
| <td class="ntext">b)</td> | <td class="ntext">b)</td> | ||
| - | <td class="ntext" width="33%">$3^{13}\cdot9^{-3}\cdot27^{-2}$</td> | + | <td class="ntext" width="33%">$3^{13}\cdot9^{-3}\cdot27^{\,-2}$</td> |
| <td class="ntext">c)</td> | <td class="ntext">c)</td> | ||
| <td class="ntext" width="33%">$\displaystyle \frac{5^{12}}{5^{-4}}\cdot(5^{2})^{-6}$</td> | <td class="ntext" width="33%">$\displaystyle \frac{5^{12}}{5^{-4}}\cdot(5^{2})^{-6}$</td> | ||
Nuvarande version
Innehåll |
[redigera] Övning 1.3:1
Beräkna
| a) | $2^3\cdot3^2$ | b) | $3^5\cdot9^{-2}$ | c) | $(-5)^3$ | d) | $\Bigl(\displaystyle \frac{2}{3}\Bigr)^{-3}$ |
Facit till alla delfrågor
| a) | $72$ | b) | $3$ | c) | $-125$ | d) | $\displaystyle \frac{27}{8}$ |
Lösning till delfråga a)
|
|
Lösning till delfråga b)
|
|
Lösning till delfråga c)
|
|
Lösning till delfråga d)
|
|
[redigera] Övning 1.3:2
Skriv som en potens av 2
| a) | $2\cdot4\cdot8$ | b) | $0{,}25$ | c) | $1$ |
Facit till alla delfrågor
| a) | $2^6$ | b) | $2^{-2}$ | c) | $2^0$ |
Lösning till delfråga a)
|
|
Lösning till delfråga b)
|
|
Lösning till delfråga c)
|
|
[redigera] Övning 1.3:3
Skriv som en potens av 3
| a) | $\displaystyle \frac{1}{3}$ | b) | $243$ | c) | $9^2$ | d) | $\displaystyle \frac{1}{27}$ | e) | $\displaystyle \frac{3}{9^2}$ |
Facit till alla delfrågor
| a) | $3^{-1}$ | b) | $3^5$ | c) | $3^4$ | d) | $3^{-3}$ | e) | $3^{-3}$ |
Lösning till delfråga a)
|
|
Lösning till delfråga b)
|
|
Lösning till delfråga c)
|
|
Lösning till delfråga d)
|
|
Lösning till delfråga e)
|
|
[redigera] Övning 1.3:4
Beräkna
| a) | $2^{9}\cdot2^{-7}$ | b) | $3^{13}\cdot9^{-3}\cdot27^{\,-2}$ | c) | $\displaystyle \frac{5^{12}}{5^{-4}}\cdot(5^{2})^{-6}$ |
| d) | $2^{2^{\scriptstyle3}}\cdot(-2)^{\scriptstyle-4}$ | e) | $625\cdot(5^{8}+5^{9})^{-1}$ | ||
Facit till alla delfrågor
| a) | $4$ | b) | $3$ | c) | $625$ |
| d) | $16$ | e) | $\displaystyle \frac{1}{3750}$ | ||
Lösning till delfråga a)
|
|
Lösning till delfråga b)
|
|
Lösning till delfråga c)
|
|
Lösning till delfråga d)
|
|
Lösning till delfråga e)
|
|
[redigera] Övning 1.3:5
Beräkna
| a) | $4^{1/2}$ | b) | $4^{-1/2}$ | c) | $9^{3/2}$ |
| d) | $\left(47^{2/3} \right) ^{3}$ | e) | $3^{1{,}4}\cdot3^{0{,}6}$ | f) | $\bigl( 125 ^{1/3} \bigr)^2\cdot \bigl( 27^{1/3} \bigr)^{-2}\cdot9^{1/2}$ |
Facit till alla delfrågor
| a) | $2$ | b) | $\displaystyle \frac{1}{2}$ | c) | $27$ |
| d) | $2209$ | e) | $9$ | f) | $\displaystyle \frac{25}{3}$ |
Lösning till delfråga a)
|
|
Lösning till delfråga b)
|
|
Lösning till delfråga c)
|
|
Lösning till delfråga d)
|
|
Lösning till delfråga e)
|
|
Lösning till delfråga f)
|
|
[redigera] Övning 1.3:6
Avgör vilket tal som är störst av
| a) | $256^{1/3}\ $ och $\ 200^{1/3}$ | b) | $0{,}5^{-3}\ $ och $\ 0{,}4^{-3}$ | c) | $0{,}2^5\ $ och $\ 0{,}2^{7}$ |
| d) | $400^{1/3}\ $ och $\ \bigl(5^{1/3}\bigr)^{4}$ | e) | $125^{1/2}\ $ och $\ 625^{1/3}$ | f) | $2^{56}\ $ och $\ 3^{40}$ |
Facit till alla delfrågor
| a) | $256^{1/3}>200^{1/3}$ | b) | $0{,}4^{-3}>0{,}5^{-3}$ | c) | $0{,}2^{5}>0{,}2^{7}$ |
| d) | $\bigl(5^{1/3}\bigr)^{4}>400^{1/3}$ | e) | $125^{1/2}>625^{1/3}$ | f) | $3^{40}>2^{56}$ |
Lösning till delfråga a)
|
|
Lösning till delfråga b)
|
|
Lösning till delfråga c)
|
|
Lösning till delfråga d)
|
|
Lösning till delfråga e)
|
|
Lösning till delfråga f)
|
|
