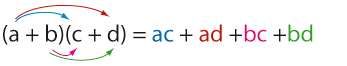2.1. Algebraiska uttryck

Sommarmatte 1

(Skillnad mellan versioner)

Hoppa till: navigering, sök

Nuvarande version

Innehåll:

Distributiva lagen
Kvadreringsreglerna
Konjugatregeln
Rationella uttryck

Lärandemål:

Efter detta avsnitt ska du ha lärt dig att:

Förenkla komplicerade algebraiska uttryck.
Faktorisera uttryck med kvadreringsreglerna och konjugatregeln.
Utveckla uttryck med kvadreringsreglerna och konjugatregeln.

[redigera] Teori

[redigera] Distributiva lagen

Den distributiva lagen anger hur man multiplicerar in en faktor i en parentes.

Exempel 1

$4 (x+y) = 4x + 4y$
$2(a-b) = 2a -2b$
$x \left(\displaystyle\frac{1}{x} + \displaystyle\frac{1}{x^2} \right) = x\cdot \displaystyle\frac{1}{x} + x \cdot \displaystyle\frac{1}{x^2} = \displaystyle\frac{\not{x}}{\not{x}} + \displaystyle\frac{\not{x}}{x^{\not{2}}} = 1 + \displaystyle\frac{1}{x}$
$a(x+y+z) = ax + ay + az$

Med den distributiva lagen kan vi också förstå hur vi kan hantera minustecken framför parentesuttryck. Regeln säger att en parentes med ett minustecken framför kan tas bort om alla termer inuti parentesen byter tecken.

Exempel 2

$-(x+y) = (-1) \cdot (x+y) = (-1)x + (-1)y = -x-y$
$-(x^2-x) = (-1) \cdot (x^2-x) = (-1)x^2 -(-1)x = -x^2 +x$

där vi i sista ledet använt att $-(-1)x = (-1)(-1)x = 1\cdot x=x$
$-(x+y-y^3) = (-1)\cdot (x+y-y^3) = (-1)\cdot x + (-1) \cdot y -(-1)\cdot y^3$
$\phantom{-(x+y-y^3)}{}=-x-y+y^3$
$x^2 - 2x -(3x+2) = x^2 -2x -3x-2 = x^2 -(2+3)x -2$
$\phantom{x^2-2x-(3x+2)}{}= x^2 -5x -2$

Om den distributiva lagen används baklänges så sägs vi faktorisera uttrycket. Ofta försöker man bryta ut en så stor faktor som möjligt.

Exempel 3

$3x +9y = 3x + 3\cdot 3y = 3(x+3y)$
$xy + y^2 = xy + y\cdot y = y(x+y)$
$2x^2 -4x = 2x\cdot x - 2\cdot 2\cdot x = 2x(x-2)$
$\displaystyle \frac{y-x}{x-y} = \displaystyle \frac{-(x-y)}{x-y} = \displaystyle \frac{-1}{1} = -1$

[redigera] Kvadreringsreglerna

Den distributiva lagen behöver ibland användas upprepade gånger för att behandla större uttryck. Om vi betraktar

$$(a+b)(c+d)$$

och ser $a+b$ som en faktor som multipliceras in i parentesen (c+d) så får vi

$$\eqalign{{\phantom{(a+b)}}\,(c+d) &= {\phantom{(a+b)}}\,c + {\phantom{(a+b)}}\,d\mbox{,}\cr (a+b)\,(c+d) &= (a+b)\,c + (a+b)\,d\mbox{.}}$$

Sedan kan $c$ och $d$ multipliceras in i respektive parentes

$$(a+b)c + (a+b)d = ac + bc + ad + bd \, \mbox{.}$$

Ett minnesvärt sätt att sammanfatta formeln är:

Exempel 4

$(x+1)(x-2) = x\cdot x + x \cdot (-2) + 1 \cdot x + 1 \cdot (-2) = x^2 -2x+x-2$
$\phantom{(x+1)(x-2)}{}=x^2 -x-2$
$3(x-y)(2x+1) = 3(x\cdot 2x + x\cdot 1 - y \cdot 2x - y \cdot 1) $
$\phantom{3(x-y)(2x+1)}{}= 3(2x^2 +x-2xy-y)=6x^2 +3x-6xy-3y$
$(1-x)(2-x) = 1\cdot 2 + 1 \cdot (-x) -x\cdot 2 - x\cdot (-x) = 2-x-2x+x^2$
$\phantom{(1-x)(2-x)}{}=2-3x+x^2$

där vi använt att $-x\cdot (-x) = (-1)x \cdot (-1)x = (-1)^2 x^2 =1\cdot x^2 = x^2$.

Två viktiga specialfall av ovanstående formel är när $\,a+b\,$ och $\,c+d\,$ är samma uttryck

Kvadreringsreglerna $$(a+b)^2 = a^2 +2ab + b^2$$ $$(a-b)^2 = a^2 -2ab + b^2$$

Dessa formler kallas för första och andra kvadreringsregeln.

Exempel 5

$(x+2)^2 = x^2 + 2\cdot 2x+ 2^2 = x^2 +4x +4$
$(-x+3)^2 = (-x)^2 + 2\cdot 3(-x) + 3^2 = x^2 -6x +9$

där $(-x)^2 = ((-1)x)^2 = (-1)^2 x^2 = 1 \cdot x^2 = x^2$
$(x^2 -4)^2 = (x^2)^2 - 2 \cdot 4x^2 + 4^2 = x^4 -8x^2 +16$
$(x+1)^2 - (x-1)^2 = (x^2 +2x +1)- (x^2-2x+1) $
$\phantom{(x+1)^2-(x-1)^2}{}= x^2 +2x +1 -x^2 + 2x-1=2x+2x=4x$
$(2x+4)(x+2) = 2(x+2)(x+2) = 2(x+2)^2 = 2(x^2 + 4x+ 4)$
$\phantom{(2x+4)(x+2)}{}=2x^2 + 8x + 8$
$(x-2)^3 = (x-2)(x-2)^2 = (x-2)(x^2-4x+4)$
$\phantom{(x-2)^3}{}=x \cdot x^2 + x\cdot (-4x) + x\cdot 4 - 2\cdot x^2 - 2 \cdot (-4x)-2 \cdot 4$
$\phantom{(x-2)^3}{}=x^3 -4x^2 + 4x-2x^2 +8x -8 = x^3-6x^2 + 12x -8$

Kvadreringsreglerna används också i omvänd riktning för att faktorisera uttryck.

Exempel 6

$x^2 + 2x+ 1 = (x+1)^2$
$x^6-4x^3 +4 = (x^3)^2 - 2\cdot 2x^3 +2^2 = (x^3-2)^2$
$x^2 +x + \frac{1}{4} = x^2 + 2\cdot\frac{1}{2}x + \bigl(\frac{1}{2}\bigr)^2 = \bigl(x+\frac{1}{2}\bigr)^2 $

[redigera] Konjugatregeln

Ett tredje specialfall av den första formeln i förra avsnittet är konjugatregeln

Konjugatregeln: $$(a+b)(a-b) = a^2 -b^2$$

Denna formel kan vi få fram direkt genom att utveckla vänsterledet

$$(a+b)(a-b)= a \cdot a + a\cdot (-b) + b\cdot a + b \cdot (-b) = a^2 -ab+ab-b^2 = a^2 -b^2\mbox{.}$$

Exempel 7

$(x-4y)(x+4y) = x^2 -(4y)^2 = x^2 -16y^2$
$(x^2+2x)(x^2-2x)= (x^2)^2 - (2x)^2 = x^4 -4x^2$
$(y+3)(3-y)= (3+y)(3-y) = 3^2 -y^2 = 9-y^2$
$x^4 -16 = (x^2)^2 -4^2 = (x^2+4)(x^2-4)= (x^2+4)(x^2-2^2)$
$\phantom{x^4-16}{}=(x^2+4)(x+2)(x-2)$

[redigera] Rationella uttryck

Räkning med algebraiska uttryck som innehåller bråk liknar till stor del vanlig bråkräkning.

Multiplikation och division av bråkuttryck följer samma räkneregler som gäller för vanliga bråktal,

$$ \frac{a}{b} \cdot \frac{c}{d} = \frac{a\cdot c}{b\cdot d} \quad \mbox{och} \quad \frac{\displaystyle\ \frac{a}{b}\ }{\displaystyle\frac{c}{d}} = \frac{a\cdot d}{b\cdot c} \; \mbox{.}$$

Exempel 8

$\displaystyle\frac{3x}{x-y} \cdot \displaystyle\frac{4x}{2x+y} = \frac{3x\cdot 4x}{(x-y)\cdot(2x+y)} = \frac{12x^2}{(x-y)(2x+y)}$
$\displaystyle \frac{\displaystyle \frac{a}{x}}{\displaystyle \frac{x+1}{a}} = \displaystyle \frac{a^2}{x(x+1)}$
$\displaystyle \frac{ \displaystyle \frac{x}{(x+1)^2}}{\displaystyle \frac{x-2}{x-1}} = \displaystyle \frac{x(x-1)}{(x-2)(x+1)^2}$

Förlängning av ett bråkuttryck innebär att vi multiplicerar täljare och nämnare med samma faktor

$$\displaystyle \frac{x+2}{x+1} = \displaystyle \frac{(x+2)(x+3)}{(x+1)(x+3)} = \displaystyle \frac{(x+2)(x+3)(x+4)}{(x+1)(x+3)(x+4) }= \dots$$

Förkortning av ett bråkuttryck innebär att vi stryker faktorer som täljaren och nämnaren har gemensamt

$$\displaystyle \frac{(x+2)(x+3)(x+4)}{(x+1)(x+3)(x+4) }= \displaystyle \frac{(x+2)(x+4)}{(x+1)(x+4)} = \displaystyle \frac{x+2}{x+1} \mbox{.}$$

Exempel 9

$\displaystyle \frac{x}{x+1} = \frac{x}{x+1} \cdot \frac{x+2}{x+2}= \frac{x(x+2)}{(x+1)(x+2)}$
$\displaystyle \frac{x^2 -1}{x(x^2-1)}= \frac{1}{x}$
$\displaystyle \frac{(x^2-y^2)(x-2)}{(x^2-4)(x+y)}= \left\{\,\text{konjugatregeln}\,\right\} = \frac{(x+y)(x-y)(x-2)}{(x+2)(x-2)(x+y)} = \frac{x-y}{x+2}$

När bråkuttryck adderas eller subtraheras behöver de, om så är nödvändigt, förlängas så att de får samma nämnare innan täljarna kan kombineras ihop,

$$\displaystyle \frac{1}{x} - \displaystyle \frac{1}{x-1} = \displaystyle \frac{1}{x} \cdot \displaystyle \frac{x-1}{x-1} - \displaystyle \frac{1}{x-1} \cdot \displaystyle \frac{x}{x} = \displaystyle \frac{x-1}{x(x-1)} - \displaystyle \frac{x}{x(x-1)} = \displaystyle \frac{x-1-x}{x(x-1)} = \displaystyle \frac{-1}{x(x-1)} \; \mbox{.}$$

Ofta försöker man förlänga med så lite som möjligt för att underlätta räknandet. Minsta gemensamma nämnare (MGN) är den gemensamma nämnare som innehåller minst antal faktorer.

Exempel 10

$\displaystyle \frac{1}{x+1} + \frac{1}{x+2}\quad$ har $\ \text{MGN}=(x+1)(x+2)$

Förläng den första termen med $(x+2)$ och den andra termen med $(x+1)$

$\displaystyle \frac{1}{x+1} + \frac{1}{x+2} = \frac{x+2}{(x+1)(x+2)} + \frac{x+1}{(x+2)(x+1)}$

$\phantom{\frac{1}{x+1} + \frac{1}{x+2}} = \displaystyle \frac{x+2+x+1}{(x+1)(x+2)} = \frac{2x+3}{(x+1)(x+2)}$
$\displaystyle \frac{1}{x} + \frac{1}{x^2}\quad$ har $\ \text{MGN}=x^2$

Vi behöver bara förlänga den första termen för att få en gemensam nämnare

$\displaystyle \frac{1}{x} + \frac{1}{x^2} = \frac{x}{x^2} + \frac{1}{x^2} = \frac{x+1}{x^2}$
$\displaystyle \frac{1}{x(x+1)^2} - \frac{1}{x^2(x+2)}\quad$ har $\ \text{MGN}= x^2(x+1)^2(x+2)$

Den första termen förlängs med $x(x+2)$ medan den andra termen förlängs med $(x+1)^2$

$\displaystyle \frac{1}{x(x+1)^2} - \frac{1}{x^2(x+2)} = \frac{x(x+2)}{x^2(x+1)^2(x+2)} - \frac{(x+1)^2}{x^2(x+1)^2(x+2)}$

$=\displaystyle \frac{x^2+2x}{x^2(x+1)^2(x+2)} - \frac{x^2+2x+1}{x^2(x+1)^2(x+2)} = \frac{x^2+2x-(x^2+2x+1)}{x^2(x+1)^2(x+2)}$

$=\displaystyle \frac{x^2+2x-x^2-2x-1}{x^2(x+1)^2(x+2)} = \frac{-1}{x^2(x+1)^2(x+2)}$
$\displaystyle \frac{x}{x+1} - \frac{1}{x(x-1)} -1 \quad$ har $\ \text{MGN}=x(x-1)(x+1)$

Vi förlänger alla termer så att de får den gemensamma nämnaren $x(x-1)(x+1)$

$\displaystyle \frac{x}{x+1} - \frac{1}{x(x-1)} -1 $

$=\displaystyle \frac{x^2(x-1)}{x(x-1)(x+1)} - \frac{x+1}{x(x-1)(x+1)} - \frac{x(x-1)(x+1)}{x(x-1)(x+1)}$

$=\displaystyle \frac{x^3-x^2}{x(x-1)(x+1)} - \frac{x+1}{x(x-1)(x+1)} -\frac{x^3 -x}{x(x-1)(x+1)}$

$=\displaystyle \frac{x^3-x^2 -(x+1) -(x^3-x)}{x(x-1)(x+1)} = \frac{x^3-x^2 -x-1 -x^3+x}{x(x-1)(x+1)} $

$= \displaystyle \frac{-x^2-1}{x(x-1)(x+1)} $

Vid förenkling av större uttryck är det ofta nödvändigt att både förlänga och förkorta i steg. Eftersom förkortning förutsätter att vi kan faktorisera uttryck är det viktigt att försöka behålla uttryck (t.ex nämnare) faktoriserade och inte utveckla något som vi senare behöver faktorisera.

Exempel 11

$\displaystyle \frac{1}{x-2} - \frac{4}{x^2-4} = \frac{1}{x-2} - \frac{4}{(x+2)(x-2)} = \left\{\,\mbox{MGN} = (x+2)(x-2)\,\right\}$

${}= \displaystyle \frac{x+2}{(x+2)(x-2)} - \frac{4}{(x+2)(x-2)} = \frac{x+2 -4}{(x+2)(x-2)}$

${}= \displaystyle \frac{x-2}{(x+2)(x-2)} = \frac{1}{x+2}$
$\displaystyle \frac{x + \displaystyle \frac{1}{x}}{x^2+1} = \frac{\displaystyle \frac{x^2}{x} + \frac{1}{x}}{x^2+1} = \frac{\displaystyle \frac{x^2+1}{x}}{x^2+1} = \frac{x^2+1}{x(x^2+1)} = \frac{1}{x}$
$\displaystyle \frac{\displaystyle \frac{1}{x^2} - \frac{1}{y^2}}{x+y} = \frac{ \displaystyle \frac{y^2}{x^2y^2} - \frac{x^2}{x^2y^2}}{x+y} = \frac{\displaystyle \frac{y^2-x^2}{x^2y^2}}{x+y} = \frac{y^2-x^2}{x^2y^2(x+y)}$

${}= \displaystyle \frac{(y+x)(y-x)}{x^2y^2(x+y)} = \frac{y-x}{x^2y^2}$

Tänk på att:

Var noggrann. Om du gör ett fel på ett ställe så kommer resten av uträkningen också vara fel.

Använd många mellanled. Om du är osäker på en uträkning utför då hellre enkla steg än ett stort steg.

Utveckla inte i onödan. Du kan vid ett senare tillfälle vara tvungen att faktorisera tillbaka.

Den här artikeln är hämtad från http://wiki.math.se/wikis/sf0600_0701/index.php/2.1._Algebraiska_uttryck

 <li>$\displaystyle \frac{1}{x+1} + \frac{1}{x+2}\quad$ har $\ \text{MGN}=(x+1)(x+2)$ <br><br>
 Förläng den första termen med $(x+2)$ och den andra termen med $(x+1)$<br/><br/>
-:$\displaystyle \frac{1}{x+1} + \frac{1}{x+2} = \frac{x+2}{(x+1)(x+2)} + \frac{x+1}{(x+2)(x+1)}= \frac{x+2+x+1}{(x+1)(x+2)} = \frac{2x+3}{(x+1)(x+2)}$ <br><br>
+:$\displaystyle \frac{1}{x+1} + \frac{1}{x+2} = \frac{x+2}{(x+1)(x+2)} + \frac{x+1}{(x+2)(x+1)}$ <br><br>
+:$\phantom{\frac{1}{x+1} + \frac{1}{x+2}} = \displaystyle \frac{x+2+x+1}{(x+1)(x+2)} = \frac{2x+3}{(x+1)(x+2)}$ <br><br>
 <li>$\displaystyle \frac{1}{x} + \frac{1}{x^2}\quad$ har $\ \text{MGN}=x^2$<br><br>
 Vi behöver bara förlänga den första termen för att få en gemensam nämnare<br/><br/>
 <li>$\displaystyle \frac{1}{x(x+1)^2} - \frac{1}{x^2(x+2)}\quad$ har $\ \text{MGN}= x^2(x+1)^2(x+2)$<br><br>
 Den första termen förlängs med $x(x+2)$ medan den andra termen förlängs med $(x+1)^2$<br/><br/>
-:$\displaystyle \frac{1}{x(x+1)^2} - \frac{1}{x^2(x+2)} = \frac{x(x+2)}{x^2(x+1)^2(x+2)} - \frac{(x+1)^2}{x^2(x+1)^2(x+2)}$ <br><br>
+$\displaystyle \frac{1}{x(x+1)^2} - \frac{1}{x^2(x+2)} = \frac{x(x+2)}{x^2(x+1)^2(x+2)} - \frac{(x+1)^2}{x^2(x+1)^2(x+2)}$ <br><br>
-::${}=\displaystyle \frac{x^2+2x}{x^2(x+1)^2(x+2)} - \frac{x^2+2x+1}{x^2(x+1)^2(x+2)} = \frac{x^2+2x-(x^2+2x+1)}{x^2(x+1)^2(x+2)}$<br><br>
+$=\displaystyle \frac{x^2+2x}{x^2(x+1)^2(x+2)} - \frac{x^2+2x+1}{x^2(x+1)^2(x+2)} = \frac{x^2+2x-(x^2+2x+1)}{x^2(x+1)^2(x+2)}$<br><br>
-::${}=\displaystyle \frac{x^2+2x-x^2-2x-1}{x^2(x+1)^2(x+2)} = \frac{-1}{x^2(x+1)^2(x+2)}$<br><br>
+$=\displaystyle \frac{x^2+2x-x^2-2x-1}{x^2(x+1)^2(x+2)} = \frac{-1}{x^2(x+1)^2(x+2)}$<br><br>
 <li>$\displaystyle \frac{x}{x+1} - \frac{1}{x(x-1)} -1 \quad$ har $\ \text{MGN}=x(x-1)(x+1)$<br><br>
 Vi förlänger alla termer så att de får den gemensamma nämnaren $x(x-1)(x+1)$<br/><br/>
-:$\displaystyle \frac{x}{x+1} - \frac{1}{x(x-1)} -1 = \frac{x^2(x-1)}{x(x-1)(x+1)} - \frac{x+1}{x(x-1)(x+1)} - \frac{x(x-1)(x+1)}{x(x-1)(x+1)}$ <br><br>
+:$\displaystyle \frac{x}{x+1} - \frac{1}{x(x-1)} -1 $<br><br>
+::$=\displaystyle \frac{x^2(x-1)}{x(x-1)(x+1)} - \frac{x+1}{x(x-1)(x+1)} - \frac{x(x-1)(x+1)}{x(x-1)(x+1)}$ <br><br>
 ::$=\displaystyle \frac{x^3-x^2}{x(x-1)(x+1)} - \frac{x+1}{x(x-1)(x+1)} -\frac{x^3 -x}{x(x-1)(x+1)}$<br><br>
 ::$=\displaystyle \frac{x^3-x^2 -(x+1) -(x^3-x)}{x(x-1)(x+1)} = \frac{x^3-x^2 -x-1 -x^3+x}{x(x-1)(x+1)} $<br><br>
 Utveckla inte i onödan. Du kan vid ett senare tillfälle vara tvungen att faktorisera tillbaka.
 </div>
+<br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br>

2.1. Algebraiska uttryck

Sommarmatte 1

Nuvarande version

[redigera] Teori

[redigera] Distributiva lagen

[redigera] Kvadreringsreglerna

[redigera] Konjugatregeln

[redigera] Rationella uttryck

Visningar

Personliga verktyg

Navigering

Sök

Verktygslåda