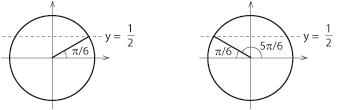4.4 Trigonometriska ekvationer
Sommarmatte 1
| Versionen från 26 april 2007 kl. 10.09 (redigera) Lina (Diskussion | bidrag) ← Gå till föregående ändring |
Nuvarande version (30 maj 2007 kl. 13.05) (redigera) (ogör) Mikael (Diskussion | bidrag) (→Grundekvationer) |
||
| (8 mellanliggande versioner visas inte.) | |||
| Rad 1: | Rad 1: | ||
| + | __NOTOC__ | ||
| <table><tr><td width="600"> | <table><tr><td width="600"> | ||
| - | |||
| - | =4.4 Trigonometriska ekvationer= | ||
| <div class="inforuta"> | <div class="inforuta"> | ||
| '''Innehåll:''' | '''Innehåll:''' | ||
| - | *Trigonometriska ekvationer | + | *Trigonometriska grundekvationer |
| + | *Enklare trigonometriska ekvationer | ||
| </div> | </div> | ||
| <div class="inforuta"> | <div class="inforuta"> | ||
| - | '''Läromål:''' | + | '''Lärandemål:''' |
| Efter detta avsnitt ska du ha lärt dig att: | Efter detta avsnitt ska du ha lärt dig att: | ||
| - | *Lösa ekvationer av typen $ \cos x = a $, $\sin x = a \;$ och $ \tan x = a $ | + | *Lösa trigonometriska grundekvationer. |
| - | *Lösa trigonometriska ekvationer som kan återföras till ovanstående ekvationer | + | *Lösa trigonometriska ekvationer som kan återföras till ovanstående ekvationstyp. |
| </div> | </div> | ||
| Rad 28: | Rad 28: | ||
| =Teori= | =Teori= | ||
| ==Grundekvationer== | ==Grundekvationer== | ||
| - | Trigonometriska ekvationer kan vara mycket komplicerade, men det finns också många typer av trigonometriska ekvationer som man kan lösa med ganska enkla metoder. Här skall vi börja med att titta på de mest grundläggande trigonometriska ekvationerna, av typerna $\sin x = a, \cos x = a $ och $\tan x = a$. | + | Trigonometriska ekvationer kan vara mycket komplicerade, men det finns också många typer av trigonometriska ekvationer som man kan lösa med ganska enkla metoder. Här skall vi börja med att titta på de mest grundläggande trigonometriska ekvationerna, av typerna $\,\sin x = a\,$, $\,\cos x = a\,$ och $\,\tan x = a\,$. |
| Dessa ekvationer har oändligt många lösningar, såvida inte omständigheterna begränsar antalet möjliga lösningar (t ex att man söker en spetsig vinkel). | Dessa ekvationer har oändligt många lösningar, såvida inte omständigheterna begränsar antalet möjliga lösningar (t ex att man söker en spetsig vinkel). | ||
| Rad 35: | Rad 35: | ||
| '''Exempel 1''' | '''Exempel 1''' | ||
| - | Lös ekvationen $\sin x = 1/2$. | + | Lös ekvationen $\ \sin x = \frac{1}{2}\,$. |
| + | <br> | ||
| + | <br> | ||
| + | Vår uppgift är att bestämma alla vinklar som gör att sinus av vinkeln blir $\,\frac{1}{2}\,$. Vi tar hjälp av enhetscirkeln. Notera att vinkeln här kallas $\,x\,$. | ||
| + | [[Bild:t_3_5_1.gif||center]] | ||
| - | '''Lösning:''' | + | I figuren har vi angivit de två riktningar som ger punkter med ''y''-koordinat $\,\frac{1}{2}\,$ i enhetscirkeln, dvs. vinklar med sinusvärdet $\,\frac{1}{2}\,$. Den första är standardvinkeln $\,30^\circ = \pi / 6\,$ och av symmetriskäl bildar den andra vinkeln $\,30^\circ\,$ mot den negativa ''x''-axeln, vilket gör att den vinkeln är $\,180^\circ – 30^\circ = 150^\circ\,$ eller i radianer $\,\pi – \pi / 6 = 5\pi / 6\,$. Detta är de enda lösningar till ekvationen $\,\sin x = \frac{1}{2}\,$ mellan $\,0\,$ och $\,2\pi\,$. |
| - | Vår uppgift är att bestämma alla vinklar som gör att sinus av vinkeln blir $1/2$. Vi tar hjälp av enhetscirkeln. Notera att vinklen här kallas $x$. | + | Vi kan dock lägga till ett godtyckligt antal varv till dessa två vinklar och fortfarande få samma sinusvärde. Alla vinklar med sinusvärde $\,\frac{1}{2}\,$ är alltså |
| - | + | ||
| - | Bild: figur 3.5.1 | + | |
| - | + | ||
| - | I figuren har vi angivit de två riktningar som ger punkter med $y$-koordinat $1/2$ i enhetscirkeln, d.v.s. vinklar med sinusvärdet $\frac{1}{2}$. Den första är standardvinkeln $30^\circ = \pi / 6 $ och symmetriskäl bildar den andra vinkeln $30^\circ$ mot den negativa $x$-axeln, vilket gör at den vinkeln är $180^\circ – 30^\circ = 150^\circ$ eller i radianer $\pi – \pi / 6 = 5\pi / 6$. Detta är de enda lösningar till ekvationen $\sin x = \frac{1}{2}$ mellan $0$ och $2\pi$. | + | |
| - | + | ||
| - | Vi kan dock lägga till ett godtyckligt antal varv till dessa två vinklar och fortfarande få samma sinusvärde. Alla vinklar med sinusvärde $\frac{1}{2}$ är alltså | + | |
| $$\left\{ \matrix{x=\displaystyle \frac{\pi}{6} + 2n\pi \\ x=\displaystyle \frac{5\pi}{6} + 2n\pi}\right.$$ | $$\left\{ \matrix{x=\displaystyle \frac{\pi}{6} + 2n\pi \\ x=\displaystyle \frac{5\pi}{6} + 2n\pi}\right.$$ | ||
| - | där $n$ är ett godtyckligt heltal. Detta kallas den fullständiga lösningen till ekvationen. | + | där $\,n\,$ är ett godtyckligt heltal. Detta kallas för den fullständiga lösningen till ekvationen. |
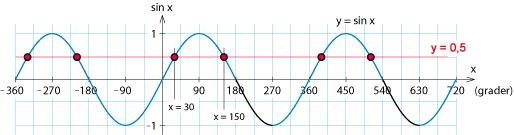
| - | Lösningarna syns också i figuren nedan där grafen till $y = \sin x$ skär linjen $y=\frac{1}{2}$. | + | Lösningarna syns också i figuren nedan där grafen till $\,y = \sin x\,$ skär linjen $\,y=\frac{1}{2}\,$. |
| - | [[Bild:3_5_02.gif]] | + | [[Bild:3_5_02.gif||center]] |
| </div> | </div> | ||
| Rad 59: | Rad 57: | ||
| '''Exempel 2''' | '''Exempel 2''' | ||
| - | Lös ekvationen $\cos x = 1/2$. | + | Lös ekvationen $\ \cos x = \frac{1}{2}\,$. |
| + | <br> | ||
| + | <br> | ||
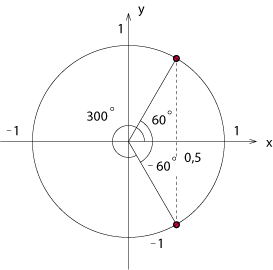
| + | Vi tar återigen hjälp av enhetscirkeln. | ||
| + | [[Bild:3_5_03.gif||center]] | ||
| - | '''Lösning:''' | + | Vi vet att cosinus blir $\,\frac{1}{2}\,$ för vinkeln $\,\pi/3\,$. Den enda andra riktning i enhetscirkeln som ger samma värde på cosinus har vinkeln $\,-\pi/3\,$. Lägger vi till ett helt antal varv till dessa vinklar får vi den fullständiga lösningen |
| - | Vi tar igen hjälp av enhetscirkeln. | + | $$x = \pm \pi/3 + n \cdot 2\pi\,\mbox{,}$$ |
| - | [[Bild:3_5_03.gif]] | + | där $\,n\,$ är ett godtyckligt heltal. |
| - | + | ||
| - | Vi vet att cosinus blir $\frac{1}{2}$ för vinkeln $\pi/3$. Den enda andra riktningen i enhetscirkeln som ger samma värde på cosinus har vinkeln $-\pi/3$. Lägger vi til ett helt antal varv till dessa vinklar får vi den fullständiga lösningen | + | |
| - | + | ||
| - | $$x = \pm \pi/3 + n \cdot 2\pi $$ | + | |
| - | + | ||
| - | där $n$ är ett godtyckligt heltal. | + | |
| </div> | </div> | ||
| Rad 79: | Rad 75: | ||
| '''Exempel 3''' | '''Exempel 3''' | ||
| - | Lös ekvationen $\tan x = \sqrt{3}$. | + | Lös ekvationen $\ \tan x = \sqrt{3}\,$. |
| + | <br> | ||
| + | <br> | ||
| + | En lösning till ekvationen är standardvinkeln $\,x=\pi/3\,$. | ||
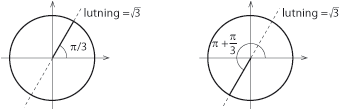
| - | '''Lösning:''' | + | Om vi betraktar enhetscirkeln så är tangens av en vinkel lika med riktningskoefficienten för den räta linje genom origo som bildar vinkeln $\,x\,$ med den positiva ''x''-axeln. |
| - | Om vi betraktar enhetscirkeln så är tangens av en vinkel lika med riktningskoefficienten för den räta linje genom origo som bildar vinkeln $x$ med den postiva $x$-axeln. | + | [[Bild:t_3_5_2.gif|center]] |
| - | Bild: figur 3.5.2 | + | Därför ser vi att lösningarna till $\,\tan x = \sqrt{3}\,$ upprepar sig varje halvt varv $\,\pi/3\,$, $\,\pi/3 +\pi\,$, $\,\pi/3+ \pi +\pi\,$ osv. Den fullständiga lösningen kan vi därmed få fram genom att utgå från lösningen $\,\pi/3\,$ och lägga till eller dra ifrån multiplar av $\,\pi\,$, |
| + | $$x = \pi/3 + n \cdot \pi\,\mbox{,}$$ | ||
| - | Därför ser vi att lösningarna till $\tan x = \sqrt{3}$ upprepar sig varje halvt varv $\pi/3, \pi/3 +\pi , \pi/3+ \pi +\pi, \ldots$ Den fullständiga lösningen kan vi få fram genom att utgå från lösningen $\pi/3$ och lägga till eller dra ifrån multiplar av $\pi$, | + | där $\,n\,$ är ett godtyckligt heltal. |
| - | $$x = \pi/3 + n \cdot \pi $$ | + | |
| - | + | ||
| - | där $n$ är ett godtyckligt heltal. | + | |
| </div> | </div> | ||
| Rad 97: | Rad 94: | ||
| Trigonometriska ekvationer kan se ut på många olika sätt, och det är omöjligt att här ge en fullständig genomgång av alla tänkbara ekvationer. Men låt oss studera några exempel, där vi kan ha nytta av att vi kan lösa grundekvationerna. | Trigonometriska ekvationer kan se ut på många olika sätt, och det är omöjligt att här ge en fullständig genomgång av alla tänkbara ekvationer. Men låt oss studera några exempel, där vi kan ha nytta av att vi kan lösa grundekvationerna. | ||
| - | Vissa trigonometriska ekvationer kan förenklas genom att de skrivs om med hjälp av trigonometriska samband. Detta kan t ex leda till en andragradsekvation, som i nedanstående exempel där man använder att $\cos 2x = 2 \cos^2 x – 1$: | + | Vissa trigonometriska ekvationer kan förenklas genom att de skrivs om med hjälp av trigonometriska samband. Detta kan t ex leda till en andragradsekvation, som i nedanstående exempel där man använder att $\,\cos 2x = 2 \cos^2\!x – 1\,$. |
| <div class="exempel"> | <div class="exempel"> | ||
| '''Exempel 4''' | '''Exempel 4''' | ||
| - | Lös ekvationen $\cos 2x – 4\cos x + 3= 0$. | + | Lös ekvationen $\ \cos 2x – 4\cos x + 3= 0\,$. |
| + | <br> | ||
| + | <br> | ||
| + | Omskrivning med hjälp av formeln $\,\cos 2x = 2 \cos^2\!x – 1\,$ ger | ||
| + | $$(2 \cos^2\!x – 1) – 4\cos x + 3 = 0\,\mbox{,}$$ | ||
| - | '''Lösning:''' | + | vilket kan förenklas till ekvationen (efter division med 2) |
| - | Omskrivning med hjälp av formeln $\cos 2x = 2 \cos^2 x – 1$ ger | + | $$\cos^2\!x - 2 \cos x +1 =0\,\mbox{.}$$ |
| - | $$(2 \cos^2 x – 1) – 4\cos x + 3 = 0$$ | + | |
| - | vilket kan förenklas till ekvationen | + | Vänsterledet kan faktoriseras med kvadreringsregeln till |
| - | $$\cos^2 x - 2 \cos x +1 =0\; \mbox{.}$$ | + | $$(\cos x-1)^2 = 0\,\mbox{.}$$ |
| - | Vänsterledet kan faktoriseras med kvaderingsreglerna till | + | Denna ekvation kan bara vara uppfylld om $\,\cos x = 1\,$. Grundekvationen $\,\cos x=1\,$ kan vi lösa på det vanliga sättet och den fullständiga lösningen är |
| - | $$(\cos x-1)^2 = 0$$ | + | $$x = 2n\pi \qquad (\,n \mbox{ godtyckligt heltal).}$$ |
| - | + | ||
| - | Denna ekvation kan bara vara uppfylld om $\cos x = 1$. Grundekvationen $\cos x=1$ kan vi lösa på det vanliga sättet och den fullständiga lösningen är | + | |
| - | + | ||
| - | $$x = 2n\pi \quad \quad(n \mbox{ godtyckligt heltal).}$$ | + | |
| </div> | </div> | ||
| - | |||
| - | Vi har nu en ekvation på formen $\cos x = a$ där'' a'' är ett tal, och där vi kan hitta lösningsmängden på vanligt sätt. | ||
| - | |||
| - | Andra ekvationer kan efter omskrivning faktoriseras, så att man får en ekvation av formen (Uttryck 1)•(Uttryck 2) = 0. De lösningsmöjligheter som då finns är att Uttryck 1 = 0 eller Uttryck 2 = 0 | ||
| <div class="exempel"> | <div class="exempel"> | ||
| '''Exempel 5''' | '''Exempel 5''' | ||
| - | Lös ekvationen $\displaystyle\frac{1}{2}\sin x + 1 – \cos^2 x = 0$. | + | Lös ekvationen $\ \frac{1}{2}\sin x + 1 – \cos^2 x = 0\,$. |
| - | + | <br> | |
| - | + | <br> | |
| - | '''Lösning:''' | + | Enligt den trigonometriska ettan är $\,\sin^2\!x + \cos^2\!x = 1\,$, dvs. $\,1 – \cos^2\!x = \sin^2\!x\,$. |
| - | + | ||
| - | Enligt trigonometriska ettan är $\sin ^2 x + \cos^2 x = 1$, dvs $1 – \cos^2 x = \sin^2 x$. | + | |
| - | + | ||
| Ekvationen kan alltså skrivas | Ekvationen kan alltså skrivas | ||
| - | $$\displaystyle\frac{1}{2}\sin x + \sin^2 x = 0\; \mbox{.}$$ | + | $$\textstyle\frac{1}{2}\sin x + \sin^2\!x = 0\,\mbox{.}$$ |
| - | + | ||
| - | Genom att nu bryta ut en faktor $\sin x$ får vi | + | |
| - | $$(\sin x )\left(\displaystyle\frac{1}{2} + \sin x\right) = 0 \; \mbox{.}$$ | + | |
| - | Från denna faktoriserade form av ekvationen ser vi att lösningarna antingen måste uppfylla $\sin x = 0$ och $\sin x = -1/2$, | + | Genom att nu bryta ut en faktor $\,\sin x\,$ får vi |
| - | vilka är två vanliga grundekvationer på formen $\sin x = a$ och kan lösas som i exempel 1. Lösningarna blir till slut | + | $$\sin x\,\cdot\,\bigl(\textstyle\frac{1}{2} + \sin x\bigr) = 0 \, \mbox{.}$$ |
| - | $$\left\{\matrix{ x=n\pi \\ x=-\frac{\pi}{6} + 2n\pi & \quad \quad (n \mbox{ godtyckligt heltal).} \\ x=\frac{7\pi}{6} + 2n\pi} \right.$$ | + | Från denna faktoriserade form av ekvationen ser vi att lösningarna antingen måste uppfylla $\,\sin x = 0\,$ eller $\,\sin x = -\frac{1}{2}\,$, vilka är två vanliga grundekvationer på formen $\,\sin x = a\,$ och kan lösas som i exempel 1. Lösningarna blir till slut |
| + | $$\left\{\eqalign{x&=n\pi\cr x&=-\pi/6+2n\pi\cr x&=7\pi/6+2n\pi\cr}\right.\qquad (\,n\ \text{godtyckligt heltal})\mbox{.}$$ | ||
| </div> | </div> | ||
| Rad 153: | Rad 140: | ||
| '''Exempel 6''' | '''Exempel 6''' | ||
| - | Lös ekvationen $\sin 2x =4 \cos x$. | + | Lös ekvationen $\ \sin 2x =4 \cos x\,$. |
| - | + | <br> | |
| - | + | <br> | |
| - | '''Lösning:''' | + | |
| - | + | ||
| Genom omskrivning med formeln för dubbla vinkeln blir ekvationen | Genom omskrivning med formeln för dubbla vinkeln blir ekvationen | ||
| + | $$2\sin x \cos x – 4 \cos x = 0\,\mbox{.}$$ | ||
| - | $2\sin x \cos x – 4 \cos x = 0$. | + | Vi delar båda led med 2 och bryter ut en faktor $\,\cos x\,$, vilket ger |
| - | + | $$\cos x\,\cdot\,( \sin x – 2) = 0\,\mbox{.}$$ | |
| - | Vi delar med 2 och bryter ut en faktor $\cos x$, vilket ger | + | |
| - | + | ||
| - | $(\cos x)( \sin x – 2) = 0$. | + | |
| Eftersom produkten bara kan bli noll genom att en faktor är noll, så kan ekvationen delas upp i grundekvationerna | Eftersom produkten bara kan bli noll genom att en faktor är noll, så kan ekvationen delas upp i grundekvationerna | ||
| + | * $\cos x = 0\,$, | ||
| + | * $\sin x = 2\,$. | ||
| - | $\cos x = 0$ och $\sin x = 2$. | + | Men $\,\sin x\,$ kan aldrig bli större än 1, så ekvationen $\,\sin x = 2\,$ saknar lösningar. Då återstår bara |
| - | + | $\,\cos x = 0\,$, vilken med hjälp av enhetscirkeln ger den fullständiga lösningen $\,x = \pi / 2 + n \cdot \pi\,$. | |
| - | Men $\sin x$ kan aldrig bli större än 1, så ekvationen $\sin x = 2$ saknar lösningar. Då återstår bara | + | |
| - | $\cos x = 0$, | + | |
| - | vilket med hjälp av enhetscirkeln ger den fullständiga lösningen | + | |
| - | $x = \pi / 2 + n \cdot \pi$. | + | |
| </div> | </div> | ||
| Rad 180: | Rad 161: | ||
| '''Exempel 7''' | '''Exempel 7''' | ||
| - | Lös ekvationen $4 \sin^2 x – 4 \cos x = 1$. | + | Lös ekvationen $\ 4 \sin^2\!x – 4 \cos x = 1\,$. |
| + | <br> | ||
| + | <br> | ||
| + | Med den trigonometriska ettan kan $\,\sin^2\!x\,$ bytas ut mot $\,1 – \cos^2\!x\,$. Då får vi | ||
| + | $$\eqalign{4 (1 – \cos^2\!x) – 4 \cos x &= 1\,\mbox{,}\cr 4 – 4 \cos^2\!x – 4 \cos x &= 1\,\mbox{,}\cr – 4 \cos^2\!x – 4 \cos x + 4 – 1 &= 0\,\mbox{,}\cr \cos^2\!x + \cos x – \textstyle\frac{3}{4} &= 0\,\mbox{.}\cr}$$ | ||
| + | Detta är en andragradsekvation i $\,\cos x\,$, som har lösningarna | ||
| + | $$\textstyle\cos x = -\frac{3}{2} \quad \mbox{och} \quad \cos x= \frac{1}{2}\,\mbox{.}$$ | ||
| - | '''Lösning:''' | + | Eftersom värdet av $\,\cos x\,$ ligger mellan $–1$ och $1$ kan ekvationen $\,\cos x=-\frac{3}{2}$ inte ha några lösningar. Då återstår bara grundekvationen |
| + | $$\cos x = \textstyle\frac{1}{2}\,\mbox{,}$$ | ||
| - | Med trigonometriska ettan kan $\sin^2 x$ bytas ut mot $1 – \cos^2 x$. Då får vi | + | som löses enligt exempel 2. |
| - | $4 (1 – \cos^2 x) – 4 \cos x = 1$ | + | </div> |
| - | $4 – 4 \cos^2 x – 4 \cos x = 1$ | + | [[4.4 Övningar|Övningar]] |
| - | $– 4 \cos^2 x – 4 \cos x + 4 – 1 = 0$ | ||
| - | $\cos^2 x + \cos x – 3/4 = 0$ | + | <div class="inforuta"> |
| + | '''Råd för inläsning''' | ||
| - | Detta är en andragradsekvation i $\cos x$, som har lösningarna | + | '''Grund- och slutprov''' |
| - | $\cos x = -\frac{3}{2} \quad \mbox{och} \quad \cos x= \frac{1}{2},$ | + | Efter att du har läst texten och arbetat med övningarna ska du göra grund- och slutprovet för att bli godkänd på detta avsnitt. Du hittar länken till proven i din student lounge. |
| - | Eftersom värdet av $\cos x $ ligger mellan – 1 och 1 kan vi förkasta alla lösningar utanför detta intervall. Då återstår bara grundekvationen | ||
| - | |||
| - | $\cos x = 1/2$, | ||
| - | |||
| - | som löses enligt exempel 2. | ||
| - | |||
| - | </div> | ||
| - | |||
| - | |||
| - | <div class="inforuta"> | ||
| - | '''Råd för inläsning''' | ||
| '''Tänk på att:''' | '''Tänk på att:''' | ||
| Rad 215: | Rad 192: | ||
| Det är bra om man lär sig de vanliga trigonometriska formlerna (identiteterna) och övar upp en viss vana på att förenkla och manipulera trigonometriska uttryck. | Det är bra om man lär sig de vanliga trigonometriska formlerna (identiteterna) och övar upp en viss vana på att förenkla och manipulera trigonometriska uttryck. | ||
| - | Det är viktigt att man lär sig de grundläggande ekvationerna, av typen sin x = a, cos x = a eller tan x = a (där a är ett reellt tal). Det är också viktigt att man vet att dessa ekvationer har oändligt många lösningar, såvida inte omständigheterna begränsar antalet möjliga lösningar (t ex att man söker en spetsig vinkel). | + | Det är viktigt att man lär sig de grundläggande ekvationerna, av typen $\,\sin x = a\,$, $\,\cos x = a\,$ eller $\,\tan x = a\,$ (där $\,a\,$ är ett reellt tal). Det är också viktigt att man vet att dessa ekvationer har oändligt många lösningar. |
| Rad 234: | Rad 211: | ||
| </div> | </div> | ||
| - | |||
| - | |||
| - | ''' © Copyright 2007, math.se''' | ||
| - | |||
| - | |||
Nuvarande version
|
Innehåll:
Lärandemål: Efter detta avsnitt ska du ha lärt dig att:
|
|
[redigera] Teori[redigera] GrundekvationerTrigonometriska ekvationer kan vara mycket komplicerade, men det finns också många typer av trigonometriska ekvationer som man kan lösa med ganska enkla metoder. Här skall vi börja med att titta på de mest grundläggande trigonometriska ekvationerna, av typerna $\,\sin x = a\,$, $\,\cos x = a\,$ och $\,\tan x = a\,$. Dessa ekvationer har oändligt många lösningar, såvida inte omständigheterna begränsar antalet möjliga lösningar (t ex att man söker en spetsig vinkel). Exempel 1 Lös ekvationen $\ \sin x = \frac{1}{2}\,$.
I figuren har vi angivit de två riktningar som ger punkter med y-koordinat $\,\frac{1}{2}\,$ i enhetscirkeln, dvs. vinklar med sinusvärdet $\,\frac{1}{2}\,$. Den första är standardvinkeln $\,30^\circ = \pi / 6\,$ och av symmetriskäl bildar den andra vinkeln $\,30^\circ\,$ mot den negativa x-axeln, vilket gör att den vinkeln är $\,180^\circ – 30^\circ = 150^\circ\,$ eller i radianer $\,\pi – \pi / 6 = 5\pi / 6\,$. Detta är de enda lösningar till ekvationen $\,\sin x = \frac{1}{2}\,$ mellan $\,0\,$ och $\,2\pi\,$. Vi kan dock lägga till ett godtyckligt antal varv till dessa två vinklar och fortfarande få samma sinusvärde. Alla vinklar med sinusvärde $\,\frac{1}{2}\,$ är alltså $$\left\{ \matrix{x=\displaystyle \frac{\pi}{6} + 2n\pi \\ x=\displaystyle \frac{5\pi}{6} + 2n\pi}\right.$$ där $\,n\,$ är ett godtyckligt heltal. Detta kallas för den fullständiga lösningen till ekvationen. Lösningarna syns också i figuren nedan där grafen till $\,y = \sin x\,$ skär linjen $\,y=\frac{1}{2}\,$. Exempel 2 Lös ekvationen $\ \cos x = \frac{1}{2}\,$.
Vi vet att cosinus blir $\,\frac{1}{2}\,$ för vinkeln $\,\pi/3\,$. Den enda andra riktning i enhetscirkeln som ger samma värde på cosinus har vinkeln $\,-\pi/3\,$. Lägger vi till ett helt antal varv till dessa vinklar får vi den fullständiga lösningen $$x = \pm \pi/3 + n \cdot 2\pi\,\mbox{,}$$ där $\,n\,$ är ett godtyckligt heltal. Exempel 3 Lös ekvationen $\ \tan x = \sqrt{3}\,$.
Om vi betraktar enhetscirkeln så är tangens av en vinkel lika med riktningskoefficienten för den räta linje genom origo som bildar vinkeln $\,x\,$ med den positiva x-axeln. Därför ser vi att lösningarna till $\,\tan x = \sqrt{3}\,$ upprepar sig varje halvt varv $\,\pi/3\,$, $\,\pi/3 +\pi\,$, $\,\pi/3+ \pi +\pi\,$ osv. Den fullständiga lösningen kan vi därmed få fram genom att utgå från lösningen $\,\pi/3\,$ och lägga till eller dra ifrån multiplar av $\,\pi\,$, $$x = \pi/3 + n \cdot \pi\,\mbox{,}$$ där $\,n\,$ är ett godtyckligt heltal. [redigera] Några mer komplicerade ekvationerTrigonometriska ekvationer kan se ut på många olika sätt, och det är omöjligt att här ge en fullständig genomgång av alla tänkbara ekvationer. Men låt oss studera några exempel, där vi kan ha nytta av att vi kan lösa grundekvationerna. Vissa trigonometriska ekvationer kan förenklas genom att de skrivs om med hjälp av trigonometriska samband. Detta kan t ex leda till en andragradsekvation, som i nedanstående exempel där man använder att $\,\cos 2x = 2 \cos^2\!x – 1\,$. Exempel 4 Lös ekvationen $\ \cos 2x – 4\cos x + 3= 0\,$.
vilket kan förenklas till ekvationen (efter division med 2) $$\cos^2\!x - 2 \cos x +1 =0\,\mbox{.}$$ Vänsterledet kan faktoriseras med kvadreringsregeln till $$(\cos x-1)^2 = 0\,\mbox{.}$$ Denna ekvation kan bara vara uppfylld om $\,\cos x = 1\,$. Grundekvationen $\,\cos x=1\,$ kan vi lösa på det vanliga sättet och den fullständiga lösningen är $$x = 2n\pi \qquad (\,n \mbox{ godtyckligt heltal).}$$ Exempel 5 Lös ekvationen $\ \frac{1}{2}\sin x + 1 – \cos^2 x = 0\,$.
Genom att nu bryta ut en faktor $\,\sin x\,$ får vi $$\sin x\,\cdot\,\bigl(\textstyle\frac{1}{2} + \sin x\bigr) = 0 \, \mbox{.}$$ Från denna faktoriserade form av ekvationen ser vi att lösningarna antingen måste uppfylla $\,\sin x = 0\,$ eller $\,\sin x = -\frac{1}{2}\,$, vilka är två vanliga grundekvationer på formen $\,\sin x = a\,$ och kan lösas som i exempel 1. Lösningarna blir till slut $$\left\{\eqalign{x&=n\pi\cr x&=-\pi/6+2n\pi\cr x&=7\pi/6+2n\pi\cr}\right.\qquad (\,n\ \text{godtyckligt heltal})\mbox{.}$$ Exempel 6 Lös ekvationen $\ \sin 2x =4 \cos x\,$.
Vi delar båda led med 2 och bryter ut en faktor $\,\cos x\,$, vilket ger $$\cos x\,\cdot\,( \sin x – 2) = 0\,\mbox{.}$$ Eftersom produkten bara kan bli noll genom att en faktor är noll, så kan ekvationen delas upp i grundekvationerna
Men $\,\sin x\,$ kan aldrig bli större än 1, så ekvationen $\,\sin x = 2\,$ saknar lösningar. Då återstår bara $\,\cos x = 0\,$, vilken med hjälp av enhetscirkeln ger den fullständiga lösningen $\,x = \pi / 2 + n \cdot \pi\,$. Exempel 7 Lös ekvationen $\ 4 \sin^2\!x – 4 \cos x = 1\,$.
Detta är en andragradsekvation i $\,\cos x\,$, som har lösningarna $$\textstyle\cos x = -\frac{3}{2} \quad \mbox{och} \quad \cos x= \frac{1}{2}\,\mbox{.}$$ Eftersom värdet av $\,\cos x\,$ ligger mellan $–1$ och $1$ kan ekvationen $\,\cos x=-\frac{3}{2}$ inte ha några lösningar. Då återstår bara grundekvationen $$\cos x = \textstyle\frac{1}{2}\,\mbox{,}$$ som löses enligt exempel 2.
Råd för inläsning Grund- och slutprov Efter att du har läst texten och arbetat med övningarna ska du göra grund- och slutprovet för att bli godkänd på detta avsnitt. Du hittar länken till proven i din student lounge.
Det är bra om man lär sig de vanliga trigonometriska formlerna (identiteterna) och övar upp en viss vana på att förenkla och manipulera trigonometriska uttryck. Det är viktigt att man lär sig de grundläggande ekvationerna, av typen $\,\sin x = a\,$, $\,\cos x = a\,$ eller $\,\tan x = a\,$ (där $\,a\,$ är ett reellt tal). Det är också viktigt att man vet att dessa ekvationer har oändligt många lösningar.
för dig som vill fördjupa dig ytterligare eller behöver en längre förklaring vill vi tipsa om: Läs mer om trigonometriska ekvationer i Theducations gymnasielexikon Träna på trigonometriska räkneexempel i Theducations gymnasielexikon
|
|