Övningar 4.1
Sommarmatte 1
| Versionen från 16 juli 2007 kl. 11.35 (redigera) KTH.SE:u1zpa8nw (Diskussion | bidrag) ← Gå till föregående ändring |
Nuvarande version (17 juli 2007 kl. 09.44) (redigera) (ogör) KTH.SE:u1zpa8nw (Diskussion | bidrag) |
||
| Rad 148: | Rad 148: | ||
| </table> | </table> | ||
| </div> | </div> | ||
| + | <br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br> | ||
Nuvarande version
Övning 4.1:1
Skriv i grader och radianer
| a) | $\displaystyle \frac{1}{4} \textrm{ varv} $ | b) | $\displaystyle \frac{3}{8} \textrm{ varv}$ |
| c) | $-\displaystyle \frac{2}{3}\textrm{ varv}$ | d) | $\displaystyle \frac{97}{12} \textrm{ varv} $ |
Övning 4.1:2
Omvandla till radianer
| a) | $45^\circ$ | b) | $135^\circ$ | c) | $-63^\circ$ | d) | $270^\circ$ |
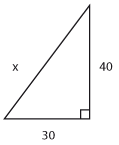
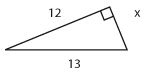
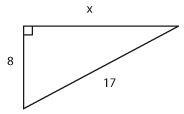
Övning 4.1:3
Bestäm längden av sidan som är markerad med $\,x$
| a) |  |
b) |  |
c) |  |
Övning 4.1:4
| a) | Bestäm avståndet mellan punkterna (1,1) och (5,4). |
| b) | Bestäm avståndet mellan punkterna (-2,5) och (3,-1). |
| c) | Hitta den punkt på x-axeln som ligger lika långt från punkterna (3,3) och (5,1). |
Övning 4.1:5
| a) | Bestäm ekvationen för en cirkel med medelpunkt i (1,2) och radie 2. |
| b) | Bestäm ekvationen för den cirkel som har medelpunkt i (2,-1) och innehåller punkten (-1,1). |
Övning 4.1:6
Skissera följande cirklar
| a) | $x^2+y^2=9$ | b) | $(x-1)^2+(y-2)^2=3$ |
| c) | $(3x-1)^2+(3y+7)^2=10$ | ||
Övning 4.1:7
Skissera följande cirklar
| a) | $x^2+2x+y^2-2y=1$ | b) | $x^2+y^2+4y=0$ |
| c) | $x^2-2x+y^2+6y=-3$ | d) | $x^2-2x+y^2+2y=-2$ |
Övning 4.1:8
Hur många varv snurrar ett hjul med radie 50 cm när det rullar 10m?
Övning 4.1:9
På en klocka är sekundvisaren 8 cm lång. Hur stor area sveper den över på 10 sekunder?
Övning 4.1:10
En 5,4 m lång tvättlina hänger mellan två vertikala träd på 4,8 m avstånd från varandra. Linans ena ände är fäst 0,6 m högre än den andra änden, och 1,2 m från trädet där linan har sin lägre infästning hänger en kavaj på en galge. Bestäm hur mycket under den nedre infästningspunkten som galgen hänger (dvs. avståndet $\,x\,$ i figuren).
|
|
