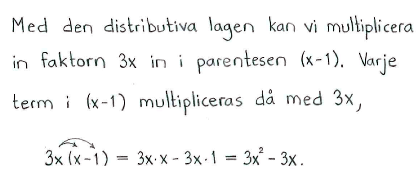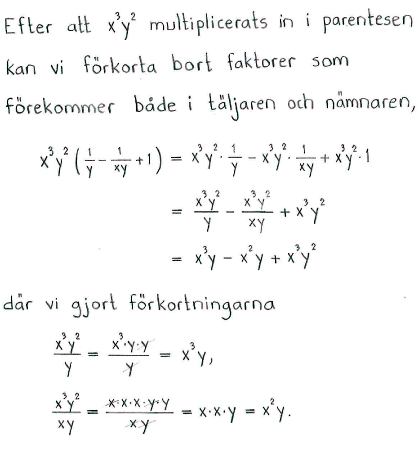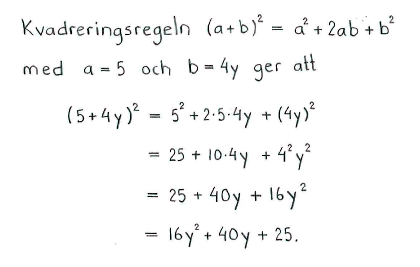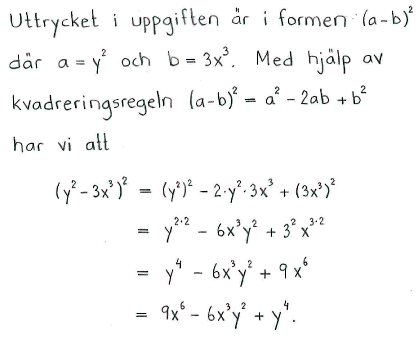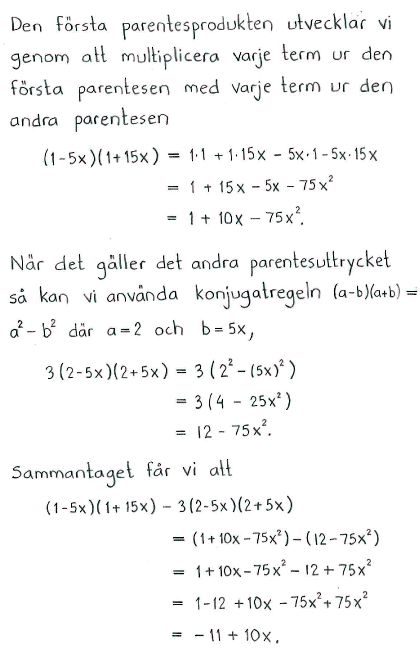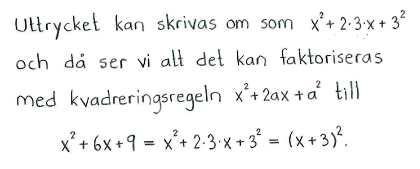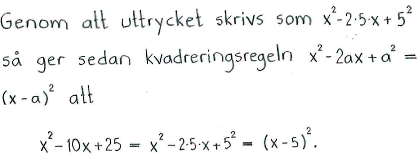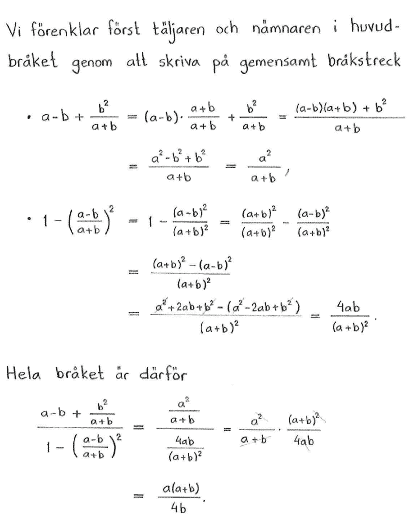2.1 Övningar
Sommarmatte 1
| Versionen från 27 april 2007 kl. 17.08 (redigera) Ossiang (Diskussion | bidrag) (→Övning 2.1:6) ← Gå till föregående ändring |
Versionen från 27 april 2007 kl. 17.09 (redigera) (ogör) Ossiang (Diskussion | bidrag) (→Övning 2.1:6) Gå till nästa ändring → |
||
| Rad 479: | Rad 479: | ||
| <td class="ntext">$2y$</td> | <td class="ntext">$2y$</td> | ||
| <td class="ntext">b)</td> | <td class="ntext">b)</td> | ||
| - | <td class="ntext">$\displaystyle-\frac{-x+12}{(x-2)(x+3)}$</td> | + | <td class="ntext">$\displaystyle\frac{-x+12}{(x-2)(x+3)}$</td> |
| </tr> | </tr> | ||
| <tr align="left"> | <tr align="left"> | ||
Versionen från 27 april 2007 kl. 17.09
Innehåll |
Övning 2.1:1
Utveckla
| a) | $3x(x-1)$ | b) | $(1+x-x^2)xy$ | c) | $-x^2(4-y^2)$ | d) | $x^3y^2\left(\displaystyle \frac{1}{y} - \frac{1}{xy}+1\right)$ |
| e) | $(x-7)^2$ | f) | $(5+4y)^2$ | g) | $(y^2-3x^3)^2$ | h) | $(5x^3+3x^5)^2$ |
Facit till alla delfrågorna
| a) | $3x^2-3x$ | b) | $xy+x^2y-x^3y$ | c) | $-4x^2+x^2y^2$ | d) | $x^3y-x^2y+x^3y^2$ |
| e) | $x^2-14x+49$ | f) | $16y^2+40y+25$ | g) | $9x^6-6x^3y^2+y^4$ | h) | $9x^{10}+30x^8+25x^6$ |
Lösning till delfråga a
Lösning till delfråga b
Lösning till delfråga c
Lösning till delfråga d
Lösning till delfråga e
Lösning till delfråga f
Lösning till delfråga g
Lösning till delfråga h
Övning 2.2:2
Utveckla och förenkla så långt som möjligt
| a) | $(x-4)(x-5)-3x(2x-3)$ | b) | $(1-5x)(1+15x)-3(2-5x)(2+5x)$ |
| c) | $(3x+4)^2-(3x-2)(3x-8)$ | d) | $(3x^2+2)(3x^2-2)(9x^4+4)$ |
| e) | $(a+b)^2+(a-b)^2$ | ||
Facit till alla delfrågorna
| a) | $-5^2+20$ | b) | $-11+10x$ |
| c) | $54x$ | d) | $81x^8-16$ |
| e) | $2a^2+2b^2$ | ||
Lösning till delfråga a 
Lösning till delfråga b 
Lösning till delfråga c 
Lösning till delfråga d 
Lösning till delfråga e 
Övning 2.1:3
Faktorisera så långt som möjligt
| $\textrm{a) }$ | $x^2-36$ | $\textrm{b) }$ | $5x^2-20$ |
| $\textrm{c) }$ | $x^2+6x+9$ | $\textrm{d) }$ | $x^2-10x+25$ |
| $\textrm{e) }$ | $18x-2x^3$ | $\textrm{f) }$ | $16x^2+8x+1$ |
Facit till alla delfrågorna
| $\textrm{a) }$ | $(x+6)(x-6)$ | $\textrm{b) }$ | $5(x+2)(x-2)$ |
| $\textrm{c) }$ | $(x+3)^2$ | $\textrm{d) }$ | $(x-5)^2$ |
| $\textrm{e) }$ | $-2x(x+3)(x-3)$ | $\textrm{f) }$ | $(4x+1)^2$ |
Lösning till delfråga a
Lösning till delfråga b
Lösning till delfråga c
Lösning till delfråga d
Lösning till delfråga e
Lösning till delfråga f
Övning 2.1:4
Bestäm koefficienterna framför $x$ och $x^2$ när följande uttryck utvecklas
| a) | $(x+2)(3x^2-x+5)$ |
| b) | $(1+x+x^2+x^3)(2-x+x^2+x^4)$ |
| c) | $(x-x^3+x^5)(1+3x+5x^2)(2-7x^2-x^4)$ |
Facit till alla delfrågorna
| a) | $5$ framför $x^2$, $3$ framför $x$ |
| b) | $2$ framför $x^2$, $1$ framför $x$ |
| $\textrm{c) }$ | $6$ framför $x^2$, $2$ framför $x$ |
Lösning till delfråga 
Lösning till delfråga 
Lösning till delfråga 
Övning 2.1:5
Förenkla så långt som möjligt
| $\textrm{a) }$ | $\displaystyle \frac{1}{x-x^2}-\displaystyle \frac{1}{x}$ | $\textrm{b) }$ | $\displaystyle \frac{1}{y^2-2y}-\displaystyle \frac{2}{y^2-4}$ |
| $\textrm{c) }$ | $\displaystyle \frac{(3x^2-12)(x^2-1)}{(x+1)(x+2)}$ | $\textrm{d) }$ | $\displaystyle \frac{(y^2+4y+4)(2y-4)}{(y^2+4)(y^2-4)}$ |
Facit till alla delfrågorna
| a) | $\displaystyle \frac{1}{1-x}$ | b) | $-\displaystyle \frac{1}{y(y+2)}$ |
| c) | $3(x-2)(x-1)$ | d) | $\displaystyle \frac{2(y+2)}{y^2+4}$ |
Lösning till delfråga a
Lösning till delfråga b
Lösning till delfråga c
Lösning till delfråga d
Övning 2.1:6
| a) | $\left(x-y+\displaystyle\frac{x^2}{y-x}\right)$ $\left(\displaystyle\frac{y}{2x-y}-1\right)$ | b) | $\displaystyle \frac{x}{x-2}+\displaystyle \frac{x}{x+3}-2$ |
| c) | $\displaystyle \frac{2a+b}{a^2-ab}-\frac{2}{a-b}$ | d) | $\displaystyle\frac{a-b+\displaystyle\frac{b^2}{a+b}}{1-\left(\displaystyle\frac{a-b}{a+b}\right)^2}$ |
Facit till alla delfrågorna
| a) | $2y$ | b) | $\displaystyle\frac{-x+12}{(x-2)(x+3)}$ |
| c) | $\displaystyle\frac{b}{a(a-b)}$ | d) | $\displaystyle\frac{a(a+b)}{4b}$ |
Lösning till delfråga a
Lösning till delfråga b
Lösning till delfråga c
Lösning till delfråga d
