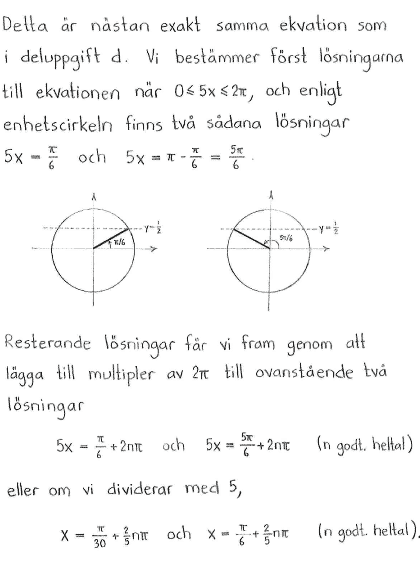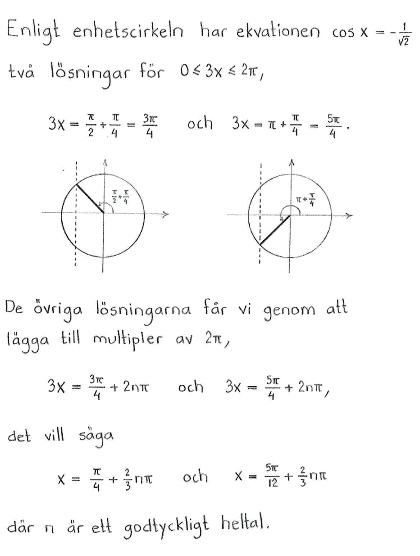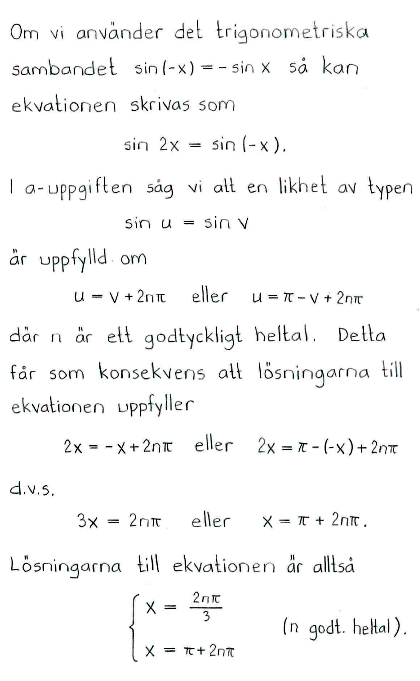4.4 Övningar
Sommarmatte 1
| Versionen från 30 april 2007 kl. 14.39 (redigera) Annagf (Diskussion | bidrag) (→Övning 4.4:6) ← Gå till föregående ändring |
Versionen från 30 april 2007 kl. 14.40 (redigera) (ogör) Annagf (Diskussion | bidrag) (→Övning 4.4:7) Gå till nästa ändring → |
||
| Rad 512: | Rad 512: | ||
| <td class="ntext">$x=\pm \displaystyle \frac{\pi}{3} + 2n\pi $</td> | <td class="ntext">$x=\pm \displaystyle \frac{\pi}{3} + 2n\pi $</td> | ||
| <td class="ntext">$\textrm{c) }$</td> | <td class="ntext">$\textrm{c) }$</td> | ||
| - | <td class="ntext">$\left\{ | + | <td class="ntext"> |
| - | \matrix{ | + | $\left\{ \matrix{ |
| x=\displaystyle \frac{\pi}{2}+2n\pi\cr | x=\displaystyle \frac{\pi}{2}+2n\pi\cr | ||
| x=\displaystyle \frac{\pi}{14}+\displaystyle \frac{2}{7}n\pi | x=\displaystyle \frac{\pi}{14}+\displaystyle \frac{2}{7}n\pi | ||
| - | } | + | }\right.$ |
| - | \right.$</td> | + | </td> |
| </tr> | </tr> | ||
| <tr><td height="5px"/></tr> | <tr><td height="5px"/></tr> | ||
| Rad 527: | Rad 527: | ||
| <div class=NavHead>Lösning a </div> | <div class=NavHead>Lösning a </div> | ||
| <div class=NavContent> | <div class=NavContent> | ||
| - | Lösning till delfråga a<br />[[Bild:4_4_6a.gif]] | + | Lösning till delfråga a<br />[[Bild:4_4_7a.gif]] |
| </div> | </div> | ||
| </div> | </div> | ||
| Rad 534: | Rad 534: | ||
| <div class=NavHead>Lösning b </DIV> | <div class=NavHead>Lösning b </DIV> | ||
| <div class=NavContent> | <div class=NavContent> | ||
| - | Lösning till delfråga b<br />[[Bild:4_4_6b.gif]] | + | Lösning till delfråga b<br />[[Bild:4_4_7b.gif]] |
| </div> | </div> | ||
| </div> | </div> | ||
| Rad 541: | Rad 541: | ||
| <div class=NavHead>Lösning c </div> | <div class=NavHead>Lösning c </div> | ||
| <div class=NavContent> | <div class=NavContent> | ||
| - | Lösning till delfråga c<br />[[Bild:4_4_6c.gif]] | + | Lösning till delfråga c<br />[[Bild:4_4_7c.gif]] |
| </div> | </div> | ||
| </div> | </div> | ||
Versionen från 30 april 2007 kl. 14.40
Innehåll |
Övning 4.4:1
För vilka vinklar $v$, där $0 \leq v\leq 2\pi$, gäller att
| $\textrm{a) }$ | $\sin{v}=\displaystyle \frac{1}{2}$ | $\textrm{b) }$ | $\cos{v}=\displaystyle \frac{1}{2}$ | $\textrm{c) }$ | $\sin{v}=1$ |
| $\textrm{d) }$ | $\tan{v}=1$ | $\textrm{e) }$ | $\cos{v}=2$ | $\textrm{f) }$ | $\sin{v}=-\displaystyle \frac{1}{2}$ |
| $\textrm{g) }$ | $\tan{v}=-\displaystyle \frac{1}{\sqrt{3}}$ | ||||
Facit till alla delfrågorna
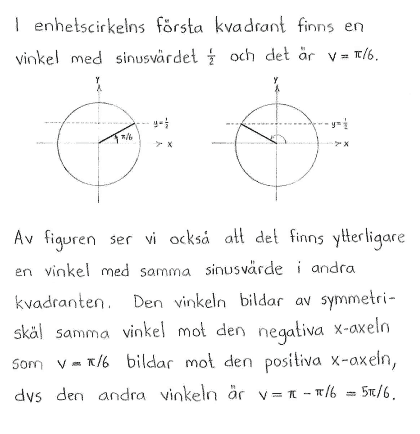
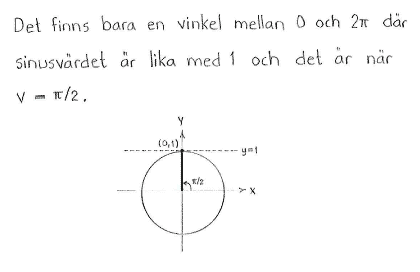
| $\textrm{a) }$ | $\displaystyle v=\frac{\pi}{6}, \displaystyle v=\frac{5\pi}{6}$ | $\textrm{b) }$ | $\displaystyle v=\frac{\pi}{3}, \displaystyle v=\frac{5\pi}{3}$ | $\textrm{c) }$ | $\displaystyle v=\frac{\pi}{2}$ |
| $\textrm{d) }$ | $\displaystyle v=\frac{\pi}{4},\displaystyle v=\frac{5\pi}{4}$ | $\textrm{e) }$ | $\textrm{lösning saknas}$ | $\textrm{f) }$ | $\displaystyle v=\frac{11\pi}{6}, \displaystyle v=\frac{7\pi}{6}$ |
| $\textrm{g) }$ | $\displaystyle v=\frac{5\pi}{6}, \displaystyle v=\frac{11\pi}{6}$ | ||||
Lösning till delfråga a
Lösning till delfråga b
Lösning till delfråga c
Lösning till delfråga d
Lösning till delfråga e
Lösning till delfråga f
Lösning till delfråga g
Bild:4 4 1g.gif
Övning 4.4:2
Lös ekvationen
| $\textrm{a) }$ | $\sin{x}=\displaystyle \frac{\sqrt{3}}{2}$ | $\textrm{b) }$ | $\cos{x}=\displaystyle \frac{1}{2} $ | $\textrm{c) }$ | $\sin{x}=0$ |
| $\textrm{d) }$ | $\sin{5x}=\displaystyle \frac{1}{\sqrt{2}} $ | $\textrm{e) }$ | $\sin{5x}=\displaystyle \frac{1}{2}$ | $\textrm{f) }$ | $\cos{3x}=-\displaystyle\frac{1}{\sqrt{2}}$ |
Facit till alla delfrågorna
| $\textrm{a) }$ |
$\left\{ \matrix{ x=\displaystyle\frac{\pi}{3}+2n\pi\cr x=\displaystyle\frac{2\pi}{3}+2n\pi } \right.$ |
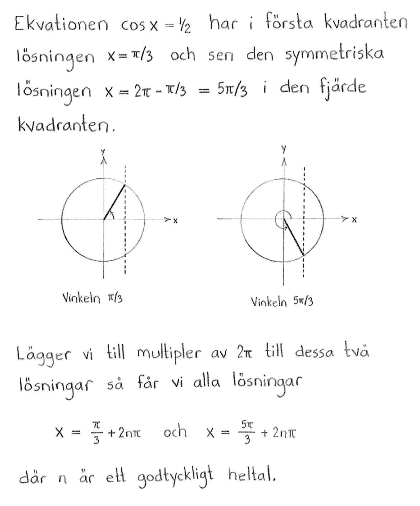
$\textrm{b) }$ |
$\left\{ \matrix{ x=\displaystyle\frac{\pi}{3}+2n\pi\cr x=\displaystyle\frac{5\pi}{3}+2n\pi } \right.$ |
$\textrm{c) }$ | $x=n\pi$ |
| $\textrm{d) }$ |
$\left\{ \matrix{ x=\displaystyle\frac{\pi}{20}+\displaystyle\frac{2n\pi}{5}\cr x=\displaystyle\frac{3\pi}{20}+\displaystyle\frac{2n\pi}{5} } \right.$ |
$\textrm{e) }$ |
$\left\{ \matrix{ x=\displaystyle\frac{\pi}{30}+\displaystyle\frac{2}{5}n\pi\cr x=\displaystyle\frac{\pi}{6}+\displaystyle\frac{2}{5}n\pi } \right.$ |
$\textrm{f) }$ | $\left\{ \matrix{x=\displaystyle\frac{\pi}{4}+\displaystyle\frac{2}{3}n\pi\cr x=\displaystyle\frac{5\pi}{12}+\displaystyle\frac{2}{3}n\pi } \right.$ |
Lösning till delfråga a
Bild:4 4 2a.gif
Lösning till delfråga b
Lösning till delfråga c
Lösning till delfråga d
Bild:4 4 2d.gif
Lösning till delfråga e
Lösning till delfråga f
Övning 4.4:3
Lös ekvationen
| $\textrm{a) }$ | $\cos{x}=\cos{\left( \displaystyle \frac{\pi}{6} \right)}$ | $\textrm{b) }$ | $\sin{x}=\sin{\left( \displaystyle \frac{\pi}{5} \right)}$ | $\textrm{c) }$ | $\sin{(x+40^\circ)}=\sin{65^\circ}$ |
| $\textrm{d) }$ | $\sin{3x}=\sin{15^\circ}$ | ||||
Facit till alla delfrågorna
| $\textrm{a) }$ |
$\left\{ \matrix{ x=\displaystyle\frac{\pi}{6}+2n\pi\cr x=\displaystyle\frac{11\pi}{6}+2n\pi }\right.$ |
$\textrm{b) }$ |
$\left\{ \matrix{ x=\displaystyle\frac{\pi}{5}+2n\pi\cr x=\displaystyle\frac{4\pi}{5}+2n\pi }\right.$ |
$\textrm{c) }$ |
$\left\{ \matrix{ x=25^\circ + n\cdot 360^\circ\cr x=75^\circ + n\cdot 360^\circ }\right.$ |
| $\textrm{d) }$ |
$\left\{ \matrix{ x=5^\circ + n \cdot 120^\circ \cr x= 55^\circ + n \cdot 120^\circ }\right.$ |
||||
Lösning till delfråga a
Lösning till delfråga b
Lösning till delfråga c
Lösning till delfråga d
Övning 4.4:4
Bestäm de vinklar $v$ i intervallet $0^\circ \leq v \leq 360^\circ$ som uppfyller $\cos{\left(2v+10^\circ\right)}=\cos{110^\circ}$.
$v=50^\circ, v=120^\circ, v=230^\circ$ och $v=300^\circ$
Övning 4.4:5
Lös ekvationen
| $\textrm{a) }$ | $\sin{3x}=\sin{x}$ | $\textrm{b) }$ | $\tan{x}=\tan{4x}$ | $\textrm{c) }$ | $\cos{5x}=\cos(x+\pi/5)$ |
Facit till alla delfrågorna
| $\textrm{a) }$ |
$\left\{ \matrix{ x=n\pi\cr x=\displaystyle \frac{\pi}{4}+\displaystyle \frac{1}{2}n\pi }\right.$ |
$\textrm{b) }$ | $x=\displaystyle \frac{1}{3}n\pi$ | $\textrm{c) }$ |
$\left\{\matrix{ x=\displaystyle \frac{\pi}{20}+\displaystyle \frac{1}{2}n\pi\cr x=-\displaystyle \frac{\pi}{30}+\displaystyle \frac{1}{3}n\pi }\right.$ |
Lösning till delfråga a
Bild:4 4 5a.gif
Lösning till delfråga b
Bild:4 4 5b.gif
Lösning till delfråga c
Bild:4 4 5c.gif
Övning 4.4:6
Lös ekvationen
| $\textrm{a) }$ | $\sin x\cdot \cos 3x = 2\sin x$ | $\textrm{b) }$ | $\sqrt{2}\sin{x}\cos{x}=\cos{x}$ | $\textrm{c) }$ | |
Facit till alla delfrågorna
| $\textrm{a) }$ |
$x=n\pi$ |
$\textrm{b) }$ |
$\left\{ \matrix{x=\displaystyle \frac{\pi}{4}+2n\pi\cr x=\displaystyle \frac{\pi}{2}+n\pi\cr x=\displaystyle \frac{3\pi}{4}+2n\pi}\right.$ |
$\textrm{c) }$ | |
Lösning till delfråga a
Lösning till delfråga b
Bild:4 4 6b.gif
Lösning till delfråga c
Övning 4.4:7
Lös ekvationen
| $\textrm{a) }$ | $2\sin^2{x}+\sin{x}=1$ | $\textrm{b) }$ | $2\sin^2{x}-3\cos{x}=0$ | $\textrm{c) }$ | $\cos{3x}=\sin{4x}$ |
Facit till alla delfrågorna
| $\textrm{a) }$ | $\left\{
\matrix{ x=\displaystyle \frac{\pi}{6}+2n\pi\cr x=\displaystyle \frac{5\pi}{6}+2n\pi\cr x=\displaystyle \frac{3\pi}{2}+2n\pi } \right.$ |
$\textrm{b) }$ | $x=\pm \displaystyle \frac{\pi}{3} + 2n\pi $ | $\textrm{c) }$ |
$\left\{ \matrix{ x=\displaystyle \frac{\pi}{2}+2n\pi\cr x=\displaystyle \frac{\pi}{14}+\displaystyle \frac{2}{7}n\pi }\right.$ |
Lösning till delfråga a
Bild:4 4 7a.gif
Lösning till delfråga b
Bild:4 4 7b.gif
Lösning till delfråga c
Bild:4 4 7c.gif
