Facit

Sommarmatte 1

(Skillnad mellan versioner)

Versionen från 16 juli 2007 kl. 08.29

Övning 1.1:1

a)	$-7$	b)	$1$
c)	$11$	d)	$1$

Övning 1.1:2

a)	$0$	b)	$-1$
c)	$-25$	d)	$-19$

Övning 1.1:3


a)	naturliga talen, heltalen, rationella talen	b)	heltalen, rationella talen	c)	naturliga talen, heltalen, rationella talen
d)	heltalen, rationella talen	e)	heltalen, rationella talen	f)	naturliga talen, heltalen, rationella talen
g)	rationella talen	h)	naturliga talen, heltalen, rationella talen	i)	irrationella talen
j)	naturliga talen, heltalen, rationella talen	k)	irrationella talen	l)	irrationella talen

Övning 1.1:4

a)	$\displaystyle \frac{3}{5}<\frac{5}{3}<2<\frac{7}{3}$
b)	$\displaystyle -\frac{1}{2}<-\frac{1}{3}<-\frac{3}{10}<-\frac{1}{5}$
c)	$\displaystyle \frac{1}{2}<\frac{3}{5}<\frac{21}{34}<\frac{5}{8}<\frac{2}{3}$

Övning 1.1:5

a)	$1{,}167$	b)	$2{,}250$	c)	$0{,}286$	d)	$1{,}414$

Övning 1.1:6

a)	Talet är rationellt och lika med $\,314/100 = 157/50\,$.
b)	Talet är rationellt och är lika med $\,31413/9999 = 10471/3333\,$.
c)	Talet är rationellt och lika med $\,1999/9990\,$.
d)	Talet är irrationellt.

Övning 1.2:1

a)	$\displaystyle \frac{93}{28}$	b)	$\displaystyle \frac{3}{35}$	c)	$\displaystyle -\frac{7}{30}$
d)	$\displaystyle \frac{47}{60}$	e)	$\displaystyle \frac{47}{84}$

Övning 1.2:2

a)	$\displaystyle {30}$	b)	$\displaystyle {8}$
c)	$\displaystyle {84}$	d)	$\displaystyle {225}$

Övning 1.2:3


a)	$\displaystyle \frac{19}{100}$	b)	$\displaystyle \frac{1}{240}$

Övning 1.2:4

a)	$\displaystyle \frac{6}{7}$	b)	$\displaystyle \frac{16}{21}$	c)	$\displaystyle \frac{1}{6}$

Övning 1.2:5


a)	$\displaystyle \frac{105}{4}$	b)	$-5$	c)	$\displaystyle \frac{8}{55}$

Övning 1.2:6

$\displaystyle \frac{152}{35}$

Övning 1.3:1

a)	$72$	b)	$3$	c)	$-125$	d)	$\displaystyle \frac{27}{8}$

Övning 1.3:2

a)	$2^6$	b)	$2^{-2}$	c)	$2^0$

Övning 1.3:3

a)	$3^{-1}$	b)	$3^5$	c)	$3^4$	d)	$3^{-3}$	e)	$3^{-3}$

Övning 1.3:4

a)	$4$	b)	$3$	c)	$625$
d)	$16$	e)	$\displaystyle \frac{1}{3750}$

Övning 1.3:5

a)	$2$	b)	$\displaystyle \frac{1}{2}$	c)	$27$
d)	$2209$	e)	$9$	f)	$\displaystyle \frac{25}{3}$

Övning 1.3:6

a)	$256^{1/3}>200^{1/3}$	b)	$0{,}4^{-3}>0{,}5^{-3}$	c)	$0{,}2^{5}>0{,}2^{7}$
d)	$\bigl(5^{1/3}\bigr)^{4}>400^{1/3}$	e)	$125^{1/2}>625^{1/3}$	f)	$3^{40}>2^{56}$

Övning 2.1:1

a)	$3x^2-3x$	b)	$xy+x^2y-x^3y$	c)	$-4x^2+x^2y^2$
d)	$x^3y-x^2y+x^3y^2$	e)	$x^2-14x+49$	f)	$16y^2+40y+25$
g)	$9x^6-6x^3y^2+y^4$	h)	$9x^{10}+30x^8+25x^6$

Övning 2.1:2

a)	$-5x^2+20$	b)	$10x-11$
c)	$54x$	d)	$81x^8-16$
e)	$2a^2+2b^2$

Övning 2.1:3

a)	$(x+6)(x-6)$	b)	$5(x+2)(x-2)$	c)	$(x+3)^2$
d)	$(x-5)^2$	e)	$-2x(x+3)(x-3)$	f)	$(4x+1)^2$

Övning 2.1:4

a)	$5\,$ framför $\,x^2\,$, $\,3\,$ framför $\,x$
b)	$2\,$ framför $\,x^2\,$, $\,1\,$ framför $\,x$
$\textrm{c) }$	$6\,$ framför $\,x^2\,$, $\,2\,$ framför $\,x$

Övning 2.1:5

a)	$\displaystyle \frac{1}{1-x}$	b)	$-\displaystyle \frac{1}{y(y+2)}$
c)	$3(x-2)(x-1)$	d)	$\displaystyle \frac{2(y+2)}{y^2+4}$

Övning 2.1:6

a)	$2y$	b)	$\displaystyle\frac{-x+12}{(x-2)(x+3)}$
c)	$\displaystyle\frac{b}{a(a-b)}$	d)	$\displaystyle\frac{a(a+b)}{4b}$

Övning 2.1:7

$\displaystyle \frac{4}{(x+3)(x+5)}$

$\displaystyle \frac{x^4-x^3+x^2+x-1}{x^2(x-1)}$

$\displaystyle \frac{ax(a+1-x)}{(a+1)^2}$

Övning 2.1:8

a)	$\displaystyle \frac{x}{(x+3)(x+1)}$	b)	$\displaystyle \frac{2(x-3)}{x}$	c)	$\displaystyle \frac{x+2}{2x+3}$

Övning 2.2:1

a)	$x=1$	b)	$x=6$
c)	$x=-\displaystyle\frac{3}{2}$	d)	$x=-\displaystyle\frac{13}{3}$

Övning 2.2:2

a)	$x=1$	b)	$x=\displaystyle\frac{5}{3}$
c)	$x=2$	d)	$x=-2$

Övning 2.2:3

a)	$x=9$
b)	$x=\displaystyle\frac{7}{5}$
c)	$x=\displaystyle\frac{4}{5}$
d)	$x=\displaystyle\frac{1}{2}$

Övning 2.2:4

a)	$-2x+y=3$
b)	$y=-\displaystyle\frac{3}{4}x+\frac{5}{4}$

Övning 2.2:5

a)	$y=-3x+9$
b)	$y=-3x+1$
c)	$y=3x+5$
d)	$y=-\displaystyle \frac{1}{2}x+5$
e)	$k = \displaystyle\frac{8}{5}$

Övning 2.2:6

a)	$\bigl(-\frac{5}{3},0\bigr)$	b)	$(0,5)$
c)	$\bigl(0,-\frac{6}{5}\bigr)$	d)	$(12,-13)$
e)	$\bigl(-\frac{1}{4},\frac{3}{2}\bigr)$

Övning 2.2:7

a)		b)
c)

Övning 2.2:8

a)		b)
c)

Övning 2.2:9

a)	$4\,$ a.e.
b)	$5\,$ a.e.
c)	$6\,$ a.e.

Övning 2.3:1

a)	$(x-1)^2-1$	b)	$(x+1)^2-2$	c)	$-(x-1)^2+6$	d)	$\bigl(x+\frac{5}{2}\bigr)^2-\frac{13}{4}$

Övning 2.3:2


a)	$\left\{ \eqalign{ x_1 &= 1 \cr x_2 &= 3\cr }\right.$	b)	$\left\{ \eqalign{ y_1 &= -5 \cr y_2 &= 3\cr }\right.$	c)	saknar (reella) lösning
d)	$ \left\{ \eqalign{ x_1 &= \textstyle\frac{1}{2}\cr x_2 &= \textstyle\frac{13}{2}\cr }\right.$	e)	$\left\{ \eqalign{ x_1 &= -1 \cr x_2 &= \textstyle\frac{3}{5}\cr }\right.$	f)	$ \left\{ \eqalign{ x_1 &= \textstyle\frac{4}{3}\cr x_2 &= 2\cr }\right.$

Övning 2.3:3

a)	$\left\{ \eqalign{ x_1 &= 0 \cr x_2 & = -3\cr }\right.$	b)	$\left\{ \eqalign{ x_1 &= 3 \cr x_2 & = -5\cr }\right. $
c)	$\left\{ \eqalign{ x_1 & = \textstyle\frac{2}{3} \cr x_2 & = -8\cr }\right. $	d)	$\left\{ \eqalign{ x_1 & = 0\cr x_2 & = 12\cr }\right. $
e)	$\left\{ \eqalign{ x_1 & = -3 \cr x_2 & = 8\cr }\right. $	f)	$\left\{ \eqalign{ x_1 & = 0 \cr x_2 & = 1 \cr x_3 & = 2 }\right. $

Övning 2.3:4

a)	$ax^2-ax-2a=0\,$, där $\,a\ne 0\,$ är en konstant.
b)	$ax^2-2ax-2a=0\,$, där $\,a\ne 0\,$ är en konstant.
c)	$ax^2-(3+\sqrt{3}\,)ax+3\sqrt{3}\,a=0\,$, där $\,a\ne 0\,$ är en konstant.

Övning 2.3:5

a)	Exempelvis $\ x^2+14x+49=0\,$.
b)	$3< x<4$
c)	$b=-5$

Övning 2.3:6

a)	$0$	b)	$-2$	c)	$\displaystyle \frac{3}{4}$

Övning 2.3:7

a)	$1$	b)	$\displaystyle -\frac{7}{4}$	c)	saknar max

Övning 2.3:8

Se lösningen i webmaterialet när du loggat in till kursen.

Övning 2.3:9

a)	$(-1,0)\ $ och $\ (1,0)$	b)	$(2,0)\ $ och $\ (3,0)$	c)	$(1,0)\ $ och $\ (3,0)$

Övning 2.3:10

Se lösningen i webmaterialet när du loggat in till kursen

Den här artikeln är hämtad från http://wiki.math.se/wikis/sf0600_0701/index.php/Facit

 </tr>
 <tr><td height="5px"/></tr>
+</table>
+</div>
+==Övning 2.1:1==
+<div class="svar">
+<table width="100%" cellspacing="10px">
+<tr align="left">
+<td class="ntext">a)</td>
+<td class="ntext" width="33%">$3x^2-3x$</td>
+<td class="ntext">b)</td>
+<td class="ntext" width="33%">$xy+x^2y-x^3y$</td>
+<td class="ntext">c)</td>
+<td class="ntext" width="33%">$-4x^2+x^2y^2$</td>
+</tr>
+<tr align="left">
+<td class="ntext">d)</td>
+<td class="ntext" width="33%">$x^3y-x^2y+x^3y^2$</td>
+<td class="ntext">e)</td>
+<td class="ntext" width="33%">$x^2-14x+49$</td>
+<td class="ntext">f)</td>
+<td class="ntext" width="33%">$16y^2+40y+25$</td>
+</tr>
+<tr align="left">
+<td class="ntext">g)</td>
+<td class="ntext" width="33%">$9x^6-6x^3y^2+y^4$</td>
+<td class="ntext">h)</td>
+<td class="ntext" width="33%">$9x^{10}+30x^8+25x^6$</td>
+</tr>
+<tr><td height="5px"/></tr>
+</table>
+</div>
+==Övning 2.1:2==
+<div class="svar">
+<table width="100%" cellspacing="10px">
+<tr align="left">
+<td class="ntext">a)</td>
+<td class="ntext" width="50%">$-5x^2+20$</td>
+<td class="ntext">b)</td>
+<td class="ntext" width="50%">$10x-11$</td>
+</tr>
+<tr align="left">
+<td class="ntext">c)</td>
+<td class="ntext" width="50%">$54x$</td>
+<td class="ntext">d)</td>
+<td class="ntext" width="50%">$81x^8-16$</td>
+</tr>
+<tr align="left">
+<td class="ntext">e)</td>
+<td class="ntext" width="50%">$2a^2+2b^2$</td>
+</tr>
+<tr><td height="5px"/></tr>
+</table>
+</div>
+==Övning 2.1:3==
+<div class="svar">
+<table width="100%" cellspacing="10px">
+<tr align="left">
+<td class="ntext">a)</td>
+<td class="ntext" width="33%">$(x+6)(x-6)$</td>
+<td class="ntext">b)</td>
+<td class="ntext" width="33%">$5(x+2)(x-2)$</td>
+<td class="ntext">c)</td>
+<td class="ntext" width="33%">$(x+3)^2$</td>
+</tr>
+<tr align="left">
+<td class="ntext">d)</td>
+<td class="ntext" width="33%">$(x-5)^2$</td>
+<td class="ntext">e)</td>
+<td class="ntext" width="33%">$-2x(x+3)(x-3)$</td>
+<td class="ntext">f)</td>
+<td class="ntext" width="33%">$(4x+1)^2$</td>
+</tr>
+<tr><td height="5px"/></tr>
+</table>
+</div>
+==Övning 2.1:4==
+<div class="svar">
+<table width="100%" cellspacing="10px">
+<tr align="left">
+<td class="ntext">a)</td>
+<td class="ntext" width="100%">$5\,$ framf&ouml;r $\,x^2\,$, $\,3\,$ framf&ouml;r $\,x$</td>
+</tr>
+<tr align="left">
+<td class="ntext">b)</td>
+<td class="ntext" width="100%">$2\,$ framf&ouml;r $\,x^2\,$, $\,1\,$ framf&ouml;r $\,x$</td>
+</tr>
+<tr align="left">
+<td class="ntext">$\textrm{c) }$</td>
+<td class="ntext" width="100%">$6\,$ framf&ouml;r $\,x^2\,$, $\,2\,$ framf&ouml;r $\,x$</td>
+</tr>
+<tr><td height="5px"/></tr>
+</table>
+</div>
+==Övning 2.1:5==
+<div class="svar">
+<table width="100%" cellspacing="10px">
+<tr align="left">
+<td class="ntext">a)</td>
+<td class="ntext" width="50%">$\displaystyle \frac{1}{1-x}$</td>
+<td class="ntext">b)</td>
+<td class="ntext" width="50%">$-\displaystyle \frac{1}{y(y+2)}$</td>
+</tr>
+<tr align="left">
+<td class="ntext">c)</td>
+<td class="ntext" width="50%">$3(x-2)(x-1)$</td>
+<td class="ntext">d)</td>
+<td class="ntext" width="50%">$\displaystyle \frac{2(y+2)}{y^2+4}$</td>
+</tr>
+</table>
+</div>
+==Övning 2.1:6==
+<div class="svar">
+<table width="100%" cellspacing="10px">
+<tr align="left">
+<td class="ntext">a)</td>
+<td class="ntext" width="50%">$2y$</td>
+<td class="ntext">b)</td>
+<td class="ntext" width="50%">$\displaystyle\frac{-x+12}{(x-2)(x+3)}$</td>
+</tr>
+<tr align="left">
+<td class="ntext">c)</td>
+<td class="ntext" width="50%">$\displaystyle\frac{b}{a(a-b)}$</td>
+<td class="ntext">d)</td>
+<td class="ntext" width="50%">$\displaystyle\frac{a(a+b)}{4b}$</td>
+</tr>
+</table>
+</div>
+==Övning 2.1:7==
+<div class="svar">
+<table width="100%" cellspacing="10px">
+<tr align="left">
+<td class="ntext">a)</td>
+<td class="ntext" width="33%">$\displaystyle \frac{4}{(x+3)(x+5)}$</td>
+<td class="ntext">b)</td>
+<td class="ntext" width="33%">$\displaystyle \frac{x^4-x^3+x^2+x-1}{x^2(x-1)}$</td>
+<td class="ntext">c)</td>
+<td class="ntext" width="33%">$\displaystyle \frac{ax(a+1-x)}{(a+1)^2}$</td>
+</tr>
+</table>
+</div>
+==Övning 2.1:8==
+<div class="svar">
+<table width="100%" cellspacing="10px">
+<tr align="left">
+<td class="ntext">a)</td>
+<td class="ntext" width="33%">$\displaystyle \frac{x}{(x+3)(x+1)}$</td>
+<td class="ntext">b)</td>
+<td class="ntext" width="33%">$\displaystyle \frac{2(x-3)}{x}$</td>
+<td class="ntext">c)</td>
+<td class="ntext" width="33%">$\displaystyle \frac{x+2}{2x+3}$</td>
+</tr>
+<tr><td height="5px"/></tr>
+</table>
+</div>
+==Övning 2.2:1==
+<div class="svar">
+<table width="100%" cellspacing="10px">
+<tr align="left">
+<td class="ntext">a)</td>
+<td class="ntext" width="50%">$x=1$</td>
+<td class="ntext">b)</td>
+<td class="ntext" width="50%">$x=6$</td>
+</tr>
+<tr align="left">
+<td class="ntext">c) </td>
+<td class="ntext" width="50%">$x=-\displaystyle\frac{3}{2}$</td>
+<td class="ntext">d)</td>
+<td class="ntext" width="50%">$x=-\displaystyle\frac{13}{3}$</td>
+</tr>
+<tr><td height="5px"/></tr>
+</table>
+</div>
+==Övning 2.2:2==
+<div class="svar">
+<table width="100%" cellspacing="10px">
+<tr align="left">
+<td class="ntext">a)</td>
+<td class="ntext" width="50%">$x=1$</td>
+<td class="ntext">b)</td>
+<td class="ntext" width="50%">$x=\displaystyle\frac{5}{3}$</td>
+</tr>
+<tr align="left">
+<td class="ntext">c)</td>
+<td class="ntext" width="50%">$x=2$</td>
+<td class="ntext">d)</td>
+<td class="ntext" width="50%">$x=-2$</td>
+</tr>
+<tr><td height="5px"/></tr>
+</table>
+</div>
+==Övning 2.2:3==
+<div class="svar">
+<table width="100%" cellspacing="10px">
+<tr align="left">
+<td class="ntext">a)</td>
+<td class="ntext" width="100%">$x=9$</td>
+</tr>
+<tr align="left">
+<td class="ntext">b)</td>
+<td class="ntext" width="100%">$x=\displaystyle\frac{7}{5}$</td>
+</tr>
+<tr align="left">
+<td class="ntext">c) </td>
+<td class="ntext" width="100%">$x=\displaystyle\frac{4}{5}$</td>
+</tr>
+<tr align="left">
+<td class="ntext">d) </td>
+<td class="ntext" width="100%">$x=\displaystyle\frac{1}{2}$</td>
+</tr>
+<tr><td height="5px"/></tr>
+</table>
+</div>
+==&Ouml;vning 2.2:4==
+<div class="svar">
+<table width="100%" cellspacing="10px">
+<tr align="left">
+<td>a)</td>
+<td width="100%">$-2x+y=3$</td>
+</tr>
+<tr align="left">
+<td>b)</td>
+<td width="100%">$y=-\displaystyle\frac{3}{4}x+\frac{5}{4}$</td>
+</tr>
+<tr><td height="5px"\></tr>
+</table>
+</div>
+==&Ouml;vning 2.2:5==
+<div class="svar">
+<table width="100%" cellspacing="10px">
+<tr align="left">
+<td class="ntext">a)</td>
+<td class="ntext" width="100%">$y=-3x+9$</td>
+</tr>
+<tr align="left">
+<td class="ntext">b)</td>
+<td class="ntext" width="100%">$y=-3x+1$</td>
+</tr>
+<tr align="left">
+<td class="ntext">c)</td>
+<td class="ntext" width="100%">$y=3x+5$</td>
+</tr>
+<tr align="left">
+<td class="ntext">d)</td>
+<td class="ntext" width="100%">$y=-\displaystyle \frac{1}{2}x+5$</td>
+</tr>
+<tr align="left">
+<td class="ntext">e)</td>
+<td class="ntext" width="100%">$k = \displaystyle\frac{8}{5}$</td>
+</tr>
+<tr><td height="5px"/></tr>
+</table>
+</div>
+==&Ouml;vning 2.2:6==
+<div class="svar">
+<table width="100%" cellspacing="10px">
+<tr align="left">
+<td class="ntext">a)</td>
+<td class="ntext" width="50%">$\bigl(-\frac{5}{3},0\bigr)$</td>
+<td class="ntext">b)</td>
+<td class="ntext" width="50%">$(0,5)$</td>
+</tr>
+<tr align="left">
+<td class="ntext">c)</td>
+<td class="ntext" width="50%">$\bigl(0,-\frac{6}{5}\bigr)$</td>
+<td class="ntext">d)</td>
+<td class="ntext" width="50%">$(12,-13)$</td>
+</tr>
+<tr align="left">
+<td class="ntext">e)</td>
+<td class="ntext" width="50%">$\bigl(-\frac{1}{4},\frac{3}{2}\bigr)$</td>
+</tr>
+<tr><td height="5px"/></tr>
+</table>
+</div>
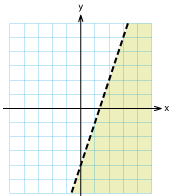
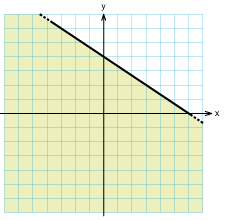
+==&Ouml;vning 2.2:7==
+<div class="svar">
+<table width="100%">
+<tr align="left">
+<td class="ntext">a)</td>
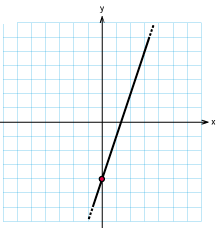
+<td class="ntext" width="33%">[[Bild:Svar_o2_2_7a.gif‎]] </td>
+<td class="ntext">b)</td>
+<td class="ntext" width="33%">[[Bild:Svar_o2_2_7b.gif‎]] </td>
+</tr><tr>
+<td class="ntext">c)</td>
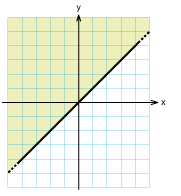
+<td class="ntext" width="33%">[[Bild:Svar_o2_2_7c.gif‎]] </td>
+</tr>
+</table>
+</div>
+==&Ouml;vning 2.2:8==
+<div class="svar">
+<table width="100%">
+<tr align="left">
+<td class="ntext">a)</td>
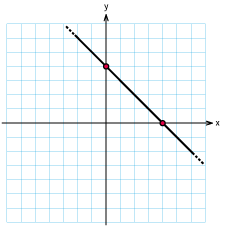
+<td class="ntext" width="33%">[[Bild:Svar_o2_2_8a.gif‎]]</td>
+<td class="ntext">b)</td>
+<td class="ntext" width="33%">[[Bild:Svar_o2_2_8b.gif‎]]</td>
+</tr><tr>
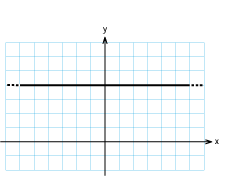
+<td class="ntext">c)</td>
+<td class="ntext" width="33%">[[Bild:Svar_o2_2_8c.gif‎]]</td>
+</tr>
+</table>
+</div>
+==&Ouml;vning 2.2:9==
+<div class="svar">
+<table width="100%" cellspacing="10px">
+<tr align="left">
+<td class="ntext">a)</td>
+<td class="ntext" width="100%">$4\,$ a.e.</td>
+</tr>
+<tr align="left">
+<td class="ntext">b)</td>
+<td class="ntext" width="100%">$5\,$ a.e.</td>
+</tr>
+<tr align="left">
+<td class="ntext">c)</td>
+<td class="ntext" width="100%">$6\,$ a.e.</td>
+</tr>
+<tr><td height="5px"/></tr>
+</table>
+</div>
+==&Ouml;vning 2.3:1==
+<div class="svar">
+<table width="100%" cellspacing="10px">
+<tr align="left">
+<td class="ntext">a)</td>
+<td class="ntext" width="25%">$(x-1)^2-1$</td>
+<td class="ntext">b)</td>
+<td class="ntext" width="25%">$(x+1)^2-2$</td>
+<td class="ntext">c)</td>
+<td class="ntext" width="25%">$-(x-1)^2+6$</td>
+<td class="ntext">d)</td>
+<td class="ntext" width="25%">$\bigl(x+\frac{5}{2}\bigr)^2-\frac{13}{4}$</td>
+</tr>
+<tr><td height="5px"/></tr>
+</table>
+</div>
+==&Ouml;vning 2.3:2==
+<div class="svar">
+<table width="100%" cellspacing="10px">
+<tr><td height="5px"/></tr>
+<tr align="left">
+<td class="ntext">a)</td>
+<td class="ntext" width="33%">$\left\{ \eqalign{ x_1 &= 1 \cr x_2 &= 3\cr }\right.$</td>
+<td class="ntext">b)</td>
+<td class="ntext" width="33%">$\left\{ \eqalign{ y_1 &= -5 \cr y_2 &= 3\cr }\right.$</td>
+<td class="ntext">c)</td>
+<td class="ntext" width="33%"> saknar (reella) l&ouml;sning</td>
+</tr>
+<tr align="left">
+<td class="ntext">d)</td>
+<td class="ntext" width="33%">$ \left\{ \eqalign{ x_1 &= \textstyle\frac{1}{2}\cr x_2 &= \textstyle\frac{13}{2}\cr }\right.$</td>
+<td class="ntext">e)</td>
+<td class="ntext" width="33%">$\left\{ \eqalign{ x_1 &= -1 \cr x_2 &= \textstyle\frac{3}{5}\cr }\right.$</td>
+<td class="ntext">f)</td>
+<td class="ntext" width="33%">$ \left\{ \eqalign{  x_1 &= \textstyle\frac{4}{3}\cr x_2 &= 2\cr }\right.$</td>
+</tr>
+<tr><td height="5px"/></tr>
+</table>
+</div>
+==&Ouml;vning 2.3:3==
+<div class="svar">
+<table width="100%" cellspacing="10px">
+<tr align="left">
+<td class="ntext">a)</td>
+<td class="ntext" width="50%">$\left\{ \eqalign{ x_1 &= 0 \cr x_2 & = -3\cr }\right.$</td>
+<td class="ntext">b)</td>
+<td class="ntext" width="50%">$\left\{ \eqalign{ x_1 &= 3 \cr x_2 & = -5\cr }\right. $</td>
+</tr>
+<tr align="left">
+<td class="ntext">c)</td>
+<td class="ntext" width="50%">$\left\{ \eqalign{  x_1 & = \textstyle\frac{2}{3} \cr x_2 & = -8\cr }\right.  $</td>
+<td class="ntext">d)</td>
+<td class="ntext" width="50%">$\left\{ \eqalign{ x_1 & = 0\cr x_2 & = 12\cr }\right.   $</td>
+</tr>
+<tr align="left">
+<td class="ntext">e)</td>
+<td class="ntext" width="50%">$\left\{ \eqalign{ x_1 & = -3 \cr x_2 & = 8\cr }\right.  $</td>
+<td class="ntext">f)</td>
+<td class="ntext" width="50%">$\left\{ \eqalign{ x_1 & = 0 \cr x_2 & = 1 \cr x_3 & = 2 }\right.   $</td>
+</tr>
+<tr><td height="5px"/></tr>
+</table>
+</div>
+==&Ouml;vning 2.3:4==
+<div class="svar">
+<table width="100%" cellspacing="10px">
+<tr align="left">
+<td class="ntext">a)</td>
+<td class="ntext" width="100%">$ax^2-ax-2a=0\,$, där $\,a\ne 0\,$ är en konstant.</td>
+</tr>
+<tr align="left">
+<td class="ntext">b)</td>
+<td class="ntext" width="100%">$ax^2-2ax-2a=0\,$, där $\,a\ne 0\,$ är en konstant.</td>
+</tr>
+<tr align="left">
+<td class="ntext">c)</td>
+<td class="ntext" width="100%">$ax^2-(3+\sqrt{3}\,)ax+3\sqrt{3}\,a=0\,$, där $\,a\ne 0\,$ är en konstant.</td>
+</tr>
+<tr><td height="5px"/></tr>
+</table>
+</div>
+==&Ouml;vning 2.3:5==
+<div class="svar">
+<table width="100%" cellspacing="10px">
+<tr align="left">
+<td class="ntext">a)</td>
+<td class="ntext" width="100%">Exempelvis $\ x^2+14x+49=0\,$.</td>
+</tr>
+<tr align="left">
+<td class="ntext">b)</td>
+<td class="ntext" width="100%">$3< x<4$</td>
+</tr>
+<tr align="left">
+<td class="ntext">c)</td>
+<td class="ntext" width="100%">$b=-5$</td>
+</tr>
+<tr><td height="5px"/></tr>
+</table>
+</div>
+==&Ouml;vning 2.3:6==
+<div class="svar">
+<table width="100%" cellspacing="10px">
+<tr align="left">
+<td class="ntext">a)</td>
+<td class="ntext" width="33%">$0$</td>
+<td class="ntext">b)</td>
+<td class="ntext" width="33%">$-2$</td>
+<td class="ntext">c)</td>
+<td class="ntext" width="33%">$\displaystyle \frac{3}{4}$</td>
+</tr>
+<tr><td height="5px"/></tr>
+</table>
+</div>
+==&Ouml;vning 2.3:7==
+<div class="svar">
+<table width="100%" cellspacing="10px">
+<tr align="left">
+<td class="ntext">a)</td>
+<td class="ntext" width="33%">$1$</td>
+<td class="ntext">b)</td>
+<td class="ntext" width="33%">$\displaystyle -\frac{7}{4}$</td>
+<td class="ntext">c)</td>
+<td class="ntext" width="33%">saknar max</td>
+</tr>
+<tr><td height="5px"/></tr>
+</table>
+</div>
+==&Ouml;vning 2.3:8==
+<div class="svar">
+<table width="100%" cellspacing="10px">
+<tr align="left">
+<td>Se lösningen i
+webmaterialet när du loggat in till kursen.</td>
+</tr>
+</table>
+</div>
+==&Ouml;vning 2.3:9==
+<div class="svar">
+<table width="100%" cellspacing="10px">
+<tr align="left">
+<td class="ntext">a)</td>
+<td class="ntext" width="33%">$(-1,0)\ $ och $\ (1,0)$</td>
+<td class="ntext">b)</td>
+<td class="ntext" width="33%">$(2,0)\ $ och $\ (3,0)$</td>
+<td class="ntext">c)</td>
+<td class="ntext" width="33%">$(1,0)\ $ och $\ (3,0)$</td>
+</tr>
+<tr><td height="5px"/></tr>
+</table>
+</div>
+==&Ouml;vning 2.3:10==
+<div class="svar">
+<table width="100%" cellspacing="10px">
+<tr align="left">
+<td>Se lösningen i webmaterialet när du loggat in till kursen</td>
+</tr>
 </table>
 </div>