3.2. Rotekvationer
Sommarmatte 1
| Versionen från 17 juli 2007 kl. 07.56 (redigera) KTH.SE:u1zpa8nw (Diskussion | bidrag) (Ny sida: __NOTOC__ <table><tr><td width="600"> <div class="inforuta"> '''Innehåll:''' *Rotekvationer av typen $\,\sqrt{ax+b}= cx +d $ *Falska rötter </div> <div class="inforuta"> '''Lärandemål...) ← Gå till föregående ändring |
Nuvarande version (17 juli 2007 kl. 09.17) (redigera) (ogör) KTH.SE:u1zpa8nw (Diskussion | bidrag) |
||
| Rad 23: | Rad 23: | ||
| <tr><td width=600> | <tr><td width=600> | ||
| <!-- huvudtexten --> | <!-- huvudtexten --> | ||
| - | |||
| =Teori= | =Teori= | ||
| Det finns många olika varianter av rotekvationer, t.ex. | Det finns många olika varianter av rotekvationer, t.ex. | ||
| Rad 102: | Rad 101: | ||
| </div> | </div> | ||
| + | |||
| + | <br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br> | ||
| + | <br><br><br><br><br><br><br><br><br> | ||
Nuvarande version
|
Innehåll:
Lärandemål: Efter detta avsnitt ska du ha lärt dig att:
|
|
[redigera] TeoriDet finns många olika varianter av rotekvationer, t.ex. $$\sqrt{x} + 3x = 2\,,$$ $$\sqrt{x - 1} - 2x = x^2\,,$$ $$\sqrt[\scriptstyle3]{x + 2} = x\,\mbox{.}$$
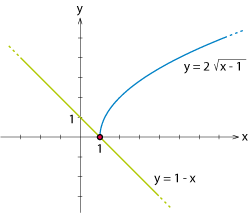
Exempel 1 Minustecken försvinner vid kvadrering. Betrakta en enkel (trivial) ekvation $$x = 2\mbox{.}$$ Om vi kvadrerar båda led i denna ekvation får vi $$x^2 = 4\mbox{.}$$ Denna nya ekvation har två lösningar $\,x = 2\,$ eller $\,x = -2\,$. Lösningen $\,x = 2\,$ uppfyller den ursprungliga ekvationen medan $\,x = -2\,$ är en lösning som uppstod i den kvadrerade ekvationen. Exempel 2 Lös ekvationen $\ 2\sqrt{x - 1} = 1 - x\,$.
Denna kan lösas med kvadratkomplettering eller med den allmänna lösningsformeln. Lösningarna blir $\,x = 3 \pm 2\,$, dvs. $\,x = 1\,$ eller $\,x = 5\,$.
Ekvationen har därmed bara en lösning $\,x = 1 \,$.
Tänk på att: När man kvadrerar en ekvation måste man tänka på att de lösningar som man får fram kanske inte är lösningar till den ursprungliga ekvationen, s. k. falska rötter. Detta beror på att eventuella minustecken försvinner. Man tappar information när man kvadrerar. Därför måste man verifiera att de lösningar man får fram, inte bara är lösningar till den kvadrerade ekvationen, utan också är lösningar till den ursprungliga ekvationen. Du ska alltid pröva lösningen i rotekvationer.
|