Övningar 4.2
Sommarmatte 1
| Versionen från 17 juli 2007 kl. 09.45 (redigera) KTH.SE:u1zpa8nw (Diskussion | bidrag) ← Gå till föregående ändring |
Nuvarande version (17 juli 2007 kl. 10.56) (redigera) (ogör) KTH.SE:u1zpa8nw (Diskussion | bidrag) |
||
| Rad 51: | Rad 51: | ||
| </table> | </table> | ||
| </div> | </div> | ||
| + | |||
| + | |||
| + | |||
| '''Övning 4.2:3''' | '''Övning 4.2:3''' | ||
Nuvarande version
Övning 4.2:1
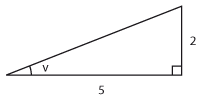
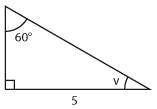
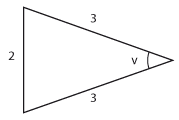
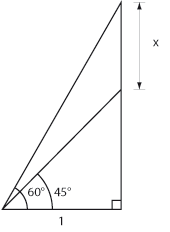
Bestäm längden av sidan som är markerad med $\,x\,$ uttryckt med hjälp av de trigonometriska funktionerna.
| a) |  |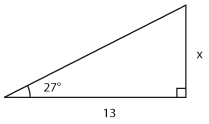
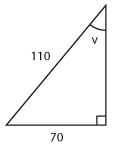
b) |  |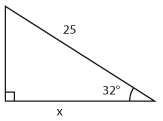
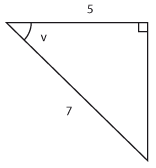
| c) |  |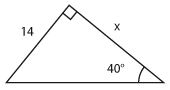
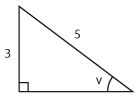
d) |  |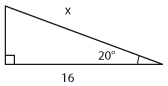
| e) |  |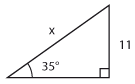
f) |  |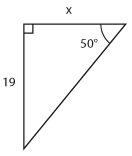
Övning 4.2:2
Bestäm en trigonometrisk ekvation som vinkeln $\,v\,$ uppfyller.
| a) |  |
b) |  |
| c) |  |
d) |  |
| e) |  |
f) |  |
Övning 4.2:3
Bestäm
| a) | $\sin{\left(-\displaystyle \frac{\pi}{2}\right)}$ | b) | $\cos{2\pi}$ | c) | $\sin{9\pi}$ |
| d) | $\cos{\displaystyle \frac{7\pi}{2}}$ | e) | $\sin{\displaystyle \frac{3\pi}{4}}$ | f) | $\cos{\left(-\displaystyle \frac{\pi}{6}\right)}$ |
Övning 4.2:4
Bestäm
| a) | $\cos{\displaystyle \frac{11\pi}{6}}$ | b) | $\cos{\displaystyle \frac{11\pi}{3}}$ | c) | $\tan{\displaystyle \frac{3\pi}{4}}$ |
| d) | $\tan{\pi}$ | e) | $\tan{\displaystyle \frac{7\pi}{6}}$ | f) | $\tan{\left(-\displaystyle \frac{5\pi}{3}\right)}$ |
Övning 4.2:5
Bestäm
| a) | $\cos{135^\circ}$ | b) | $\tan{225^\circ}$ | c) | $\cos{330^\circ}$ | d) | $\tan{495^\circ}$ |
Övning 4.2:6
Bestäm längden av sidan som är markerad med $\,x\,$.
 |
Övning 4.2:7
För att mäta upp bredden av en älv mäter vi från två punkter A och B längs den ena raka stranden vinkeln till ett träd C på motsatt sida älven. Hur bred är älven om måtten i figuren gäller?
 |
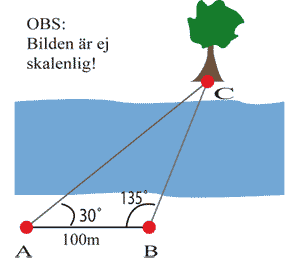Övning 4.2:8
En stång med längd $\,\ell\,$ är upphängd i två linor med längd $\,a\,$ resp. $\,b\,$ enligt figuren. Linorna bildar vinklar $\,\alpha\,$ resp. $\,\beta\,$ med vertikalen. Bestäm en trigonometrisk ekvation för vinkeln $\,\gamma\,$ som stången bildar med vertikalen.
 |
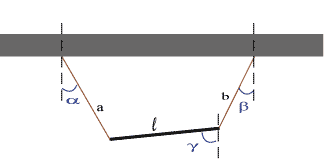Övning 4.2:9
Bilvägen från A till B består av tre rätlinjiga delar AP, PQ och QB, vilka är 4,0 km, 12,0 km respektive 5,0 km. De i figuren markerade vinklarna vid P och Q är 30° respektive 90°. Beräkna avståndet fågelvägen från A till B. (Uppgiften är hämtad ur Centrala provet i matematik, november 1976, men aningen modifierad.)
 |
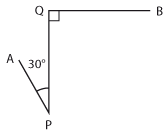