Övningar 1.1
Sommarmatte 1
(Skillnad mellan versioner)
| Versionen från 18 juli 2007 kl. 08.06 (redigera) KTH.SE:u1zpa8nw (Diskussion | bidrag) ← Gå till föregående ändring |
Versionen från 18 juli 2007 kl. 08.07 (redigera) (ogör) KTH.SE:u1zpa8nw (Diskussion | bidrag) Gå till nästa ändring → |
||
| Rad 1: | Rad 1: | ||
| '''Övning 1.1:1''' | '''Övning 1.1:1''' | ||
| - | <div class="ovning" style="margin-top:-20px; margin-bottom:-5px;"> | + | <div class="ovning" style="margin-top:-20px; margin-bottom:-10px;"> |
| Grafen till $f(x)$ är ritad i figuren. <br\> | Grafen till $f(x)$ är ritad i figuren. <br\> | ||
| [[Bild:o_1_1_1a.gif]] | [[Bild:o_1_1_1a.gif]] | ||
| Rad 21: | Rad 21: | ||
| '''Övning 1.1:2''' | '''Övning 1.1:2''' | ||
| - | <div class="ovning" style="margin-top:-20px; margin-bottom:-5px;"> | + | <div class="ovning" style="margin-top:-20px; margin-bottom:-10px;"> |
| Bestäm $f'(x)$ om | Bestäm $f'(x)$ om | ||
| <table width="100%" cellspacing="10px"> | <table width="100%" cellspacing="10px"> | ||
| Rad 44: | Rad 44: | ||
| '''Övning 1.1:3''' | '''Övning 1.1:3''' | ||
| - | <div class="ovning" style="margin-top:-20px; margin-bottom:-5px;"> | + | <div class="ovning" style="margin-top:-20px; margin-bottom:-10px;"> |
| En liten boll som släpps från höjden $h=10$m ovanför marken vid tidpunkten $t=0$, har vid tiden $t$ (mätt i sekunder) höjden $h(t)=10-\displaystyle\frac{9,\!82}{2}\,t^2$. Vilken fart har bollen när den slår i backen? | En liten boll som släpps från höjden $h=10$m ovanför marken vid tidpunkten $t=0$, har vid tiden $t$ (mätt i sekunder) höjden $h(t)=10-\displaystyle\frac{9,\!82}{2}\,t^2$. Vilken fart har bollen när den slår i backen? | ||
| + | </div> | ||
| + | |||
| + | <div class=NavFrame style="CLEAR: both"> | ||
| + | <div class=NavHead>Facit </div> | ||
| + | <div class=NavContent> | ||
| + | <table width="100%" cellspacing="10px"> | ||
| + | <tr align="left"> | ||
| + | <td class="ntext" width="100%">$14{,}0\,$ m/s</td> | ||
| + | </tr> | ||
| + | <tr><td height="5px"/></tr> | ||
| + | </table> | ||
| + | </div> | ||
| </div> | </div> | ||
| '''Övning 1.1:4''' | '''Övning 1.1:4''' | ||
| - | <div class="ovning" style="margin-top:-20px; margin-bottom:-5px;"> | + | <div class="ovning" style="margin-top:-20px; margin-bottom:-10px;"> |
| Bestäm ekvationen för tangenten och normalen till kurvan $y=x^2$ i punkten $(1,1)$. | Bestäm ekvationen för tangenten och normalen till kurvan $y=x^2$ i punkten $(1,1)$. | ||
| </div> | </div> | ||
| '''Övning 1.1:5''' | '''Övning 1.1:5''' | ||
| - | <div class="ovning" style="margin-top:-20px; margin-bottom:-5px;"> | + | <div class="ovning" style="margin-top:-20px; margin-bottom:-10px;"> |
| Bestäm alla punkter på kurvan $y=-x^2$ som har en tangent som går genom punkten $(1,1)$. | Bestäm alla punkter på kurvan $y=-x^2$ som har en tangent som går genom punkten $(1,1)$. | ||
| </div> | </div> | ||
| - | |||
| - | <br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br> | ||
Versionen från 18 juli 2007 kl. 08.07
Övning 1.1:1
Grafen till $f(x)$ är ritad i figuren.
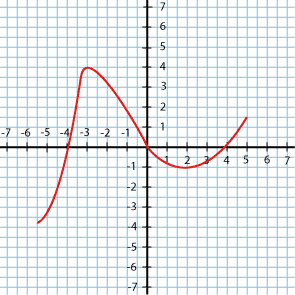
| a) | Vilket tecken har $f'(-4)$ respektive $f'(1)$? |
| b) | För vilka $x$-värden är $f'(x)=0$? |
| c) | I vilket eller vilka intervall är $f'(x)$ negativ? |
Övning 1.1:2
Bestäm $f'(x)$ om
| a) | $f(x) = x^2 -3x +1$ | b) | $f(x)=\cos x -\sin x$ | c) | $f(x)= e^x-\ln x$ |
| d) | $f(x)=\sqrt{x}$ | e) | $f(x) = (x^2-1)^2$ | f) | $f(x)= \cos (x+\pi/3)$ |
Övning 1.1:3
En liten boll som släpps från höjden $h=10$m ovanför marken vid tidpunkten $t=0$, har vid tiden $t$ (mätt i sekunder) höjden $h(t)=10-\displaystyle\frac{9,\!82}{2}\,t^2$. Vilken fart har bollen när den slår i backen?
Facit
| $14{,}0\,$ m/s |
Övning 1.1:4
Bestäm ekvationen för tangenten och normalen till kurvan $y=x^2$ i punkten $(1,1)$.
Övning 1.1:5
Bestäm alla punkter på kurvan $y=-x^2$ som har en tangent som går genom punkten $(1,1)$.

