Facit
Sommarmatte 1
Övning 1.1:1
| a) | $-7$ | b) | $1$ |
| c) | $11$ | d) | $1$ |
Övning 1.1:2
| a) | $0$ | b) | $-1$ |
| c) | $-25$ | d) | $-19$ |
Övning 1.1:3
| a) | naturliga talen, heltalen, rationella talen | b) | heltalen, rationella talen | c) | naturliga talen, heltalen, rationella talen |
| d) | heltalen, rationella talen | e) | heltalen, rationella talen | f) | naturliga talen, heltalen, rationella talen |
| g) | rationella talen | h) | naturliga talen, heltalen, rationella talen | i) | irrationella talen |
| j) | naturliga talen, heltalen, rationella talen | k) | irrationella talen | l) | irrationella talen |
Övning 1.1:4
| a) | $\displaystyle \frac{3}{5}<\frac{5}{3}<2<\frac{7}{3}$ |
| b) | $\displaystyle -\frac{1}{2}<-\frac{1}{3}<-\frac{3}{10}<-\frac{1}{5}$ |
| c) | $\displaystyle \frac{1}{2}<\frac{3}{5}<\frac{21}{34}<\frac{5}{8}<\frac{2}{3}$ |
Övning 1.1:5
| a) | $1{,}167$ | b) | $2{,}250$ | c) | $0{,}286$ | d) | $1{,}414$ |
Övning 1.1:6
| a) | Talet är rationellt och lika med $\,314/100 = 157/50\,$. |
| b) | Talet är rationellt och är lika med $\,31413/9999 = 10471/3333\,$. |
| c) | Talet är rationellt och lika med $\,1999/9990\,$. |
| d) | Talet är irrationellt. |
Övning 1.2:1
| a) | $\displaystyle \frac{93}{28}$ | b) | $\displaystyle \frac{3}{35}$ | c) | $\displaystyle -\frac{7}{30}$ |
| d) | $\displaystyle \frac{47}{60}$ | e) | $\displaystyle \frac{47}{84}$ | ||
Övning 1.2:2
| a) | $\displaystyle {30}$ | b) | $\displaystyle {8}$ |
| c) | $\displaystyle {84}$ | d) | $\displaystyle {225}$ |
Övning 1.2:3
| a) | $\displaystyle \frac{19}{100}$ | b) | $\displaystyle \frac{1}{240}$ |
Övning 1.2:4
| a) | $\displaystyle \frac{6}{7}$ | b) | $\displaystyle \frac{16}{21}$ | c) | $\displaystyle \frac{1}{6}$ |
Övning 1.2:5
| a) | $\displaystyle \frac{105}{4}$ | b) | $-5$ | c) | $\displaystyle \frac{8}{55}$ |
Övning 1.2:6
| $\displaystyle \frac{152}{35}$ |
Övning 1.3:1
| a) | $72$ | b) | $3$ | c) | $-125$ | d) | $\displaystyle \frac{27}{8}$ |
Övning 1.3:2
| a) | $2^6$ | b) | $2^{-2}$ | c) | $2^0$ |
Övning 1.3:3
| a) | $3^{-1}$ | b) | $3^5$ | c) | $3^4$ | d) | $3^{-3}$ | e) | $3^{-3}$ |
Övning 1.3:4
| a) | $4$ | b) | $3$ | c) | $625$ |
| d) | $16$ | e) | $\displaystyle \frac{1}{3750}$ | ||
Övning 1.3:5
| a) | $2$ | b) | $\displaystyle \frac{1}{2}$ | c) | $27$ |
| d) | $2209$ | e) | $9$ | f) | $\displaystyle \frac{25}{3}$ |
Övning 1.3:6
| a) | $256^{1/3}>200^{1/3}$ | b) | $0{,}4^{-3}>0{,}5^{-3}$ | c) | $0{,}2^{5}>0{,}2^{7}$ |
| d) | $\bigl(5^{1/3}\bigr)^{4}>400^{1/3}$ | e) | $125^{1/2}>625^{1/3}$ | f) | $3^{40}>2^{56}$ |
Övning 2.1:1
| a) | $3x^2-3x$ | b) | $xy+x^2y-x^3y$ | c) | $-4x^2+x^2y^2$ |
| d) | $x^3y-x^2y+x^3y^2$ | e) | $x^2-14x+49$ | f) | $16y^2+40y+25$ |
| g) | $9x^6-6x^3y^2+y^4$ | h) | $9x^{10}+30x^8+25x^6$ | ||
Övning 2.1:2
| a) | $-5x^2+20$ | b) | $10x-11$ |
| c) | $54x$ | d) | $81x^8-16$ |
| e) | $2a^2+2b^2$ | ||
Övning 2.1:3
| a) | $(x+6)(x-6)$ | b) | $5(x+2)(x-2)$ | c) | $(x+3)^2$ |
| d) | $(x-5)^2$ | e) | $-2x(x+3)(x-3)$ | f) | $(4x+1)^2$ |
Övning 2.1:4
| a) | $5\,$ framför $\,x^2\,$, $\,3\,$ framför $\,x$ |
| b) | $2\,$ framför $\,x^2\,$, $\,1\,$ framför $\,x$ |
| $\textrm{c) }$ | $6\,$ framför $\,x^2\,$, $\,2\,$ framför $\,x$ |
Övning 2.1:5
| a) | $\displaystyle \frac{1}{1-x}$ | b) | $-\displaystyle \frac{1}{y(y+2)}$ |
| c) | $3(x-2)(x-1)$ | d) | $\displaystyle \frac{2(y+2)}{y^2+4}$ |
Övning 2.1:6
| a) | $2y$ | b) | $\displaystyle\frac{-x+12}{(x-2)(x+3)}$ |
| c) | $\displaystyle\frac{b}{a(a-b)}$ | d) | $\displaystyle\frac{a(a+b)}{4b}$ |
Övning 2.1:7
| a) | $\displaystyle \frac{4}{(x+3)(x+5)}$ | b) | $\displaystyle \frac{x^4-x^3+x^2+x-1}{x^2(x-1)}$ | c) | $\displaystyle \frac{ax(a+1-x)}{(a+1)^2}$ |
Övning 2.1:8
| a) | $\displaystyle \frac{x}{(x+3)(x+1)}$ | b) | $\displaystyle \frac{2(x-3)}{x}$ | c) | $\displaystyle \frac{x+2}{2x+3}$ |
Övning 2.2:1
| a) | $x=1$ | b) | $x=6$ |
| c) | $x=-\displaystyle\frac{3}{2}$ | d) | $x=-\displaystyle\frac{13}{3}$ |
Övning 2.2:2
| a) | $x=1$ | b) | $x=\displaystyle\frac{5}{3}$ |
| c) | $x=2$ | d) | $x=-2$ |
Övning 2.2:3
| a) | $x=9$ |
| b) | $x=\displaystyle\frac{7}{5}$ |
| c) | $x=\displaystyle\frac{4}{5}$ |
| d) | $x=\displaystyle\frac{1}{2}$ |
Övning 2.2:4
| a) | $-2x+y=3$ |
| b) | $y=-\displaystyle\frac{3}{4}x+\frac{5}{4}$ |
Övning 2.2:5
| a) | $y=-3x+9$ |
| b) | $y=-3x+1$ |
| c) | $y=3x+5$ |
| d) | $y=-\displaystyle \frac{1}{2}x+5$ |
| e) | $k = \displaystyle\frac{8}{5}$ |
Övning 2.2:6
| a) | $\bigl(-\frac{5}{3},0\bigr)$ | b) | $(0,5)$ |
| c) | $\bigl(0,-\frac{6}{5}\bigr)$ | d) | $(12,-13)$ |
| e) | $\bigl(-\frac{1}{4},\frac{3}{2}\bigr)$ | ||
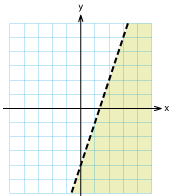
Övning 2.2:7
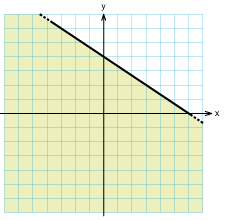
Övning 2.2:8
Övning 2.2:9
| a) | $4\,$ a.e. |
| b) | $5\,$ a.e. |
| c) | $6\,$ a.e. |
Övning 2.3:1
| a) | $(x-1)^2-1$ | b) | $(x+1)^2-2$ | c) | $-(x-1)^2+6$ | d) | $\bigl(x+\frac{5}{2}\bigr)^2-\frac{13}{4}$ |
Övning 2.3:2
| a) | $\left\{ \eqalign{ x_1 &= 1 \cr x_2 &= 3\cr }\right.$ | b) | $\left\{ \eqalign{ y_1 &= -5 \cr y_2 &= 3\cr }\right.$ | c) | saknar (reella) lösning |
| d) | $ \left\{ \eqalign{ x_1 &= \textstyle\frac{1}{2}\cr x_2 &= \textstyle\frac{13}{2}\cr }\right.$ | e) | $\left\{ \eqalign{ x_1 &= -1 \cr x_2 &= \textstyle\frac{3}{5}\cr }\right.$ | f) | $ \left\{ \eqalign{ x_1 &= \textstyle\frac{4}{3}\cr x_2 &= 2\cr }\right.$ |
Övning 2.3:3
| a) | $\left\{ \eqalign{ x_1 &= 0 \cr x_2 & = -3\cr }\right.$ | b) | $\left\{ \eqalign{ x_1 &= 3 \cr x_2 & = -5\cr }\right. $ |
| c) | $\left\{ \eqalign{ x_1 & = \textstyle\frac{2}{3} \cr x_2 & = -8\cr }\right. $ | d) | $\left\{ \eqalign{ x_1 & = 0\cr x_2 & = 12\cr }\right. $ |
| e) | $\left\{ \eqalign{ x_1 & = -3 \cr x_2 & = 8\cr }\right. $ | f) | $\left\{ \eqalign{ x_1 & = 0 \cr x_2 & = 1 \cr x_3 & = 2 }\right. $ |
Övning 2.3:4
| a) | $ax^2-ax-2a=0\,$, där $\,a\ne 0\,$ är en konstant. |
| b) | $ax^2-2ax-2a=0\,$, där $\,a\ne 0\,$ är en konstant. |
| c) | $ax^2-(3+\sqrt{3}\,)ax+3\sqrt{3}\,a=0\,$, där $\,a\ne 0\,$ är en konstant. |
Övning 2.3:5
| a) | Exempelvis $\ x^2+14x+49=0\,$. |
| b) | $3< x<4$ |
| c) | $b=-5$ |
Övning 2.3:6
| a) | $0$ | b) | $-2$ | c) | $\displaystyle \frac{3}{4}$ |
Övning 2.3:7
| a) | $1$ | b) | $\displaystyle -\frac{7}{4}$ | c) | saknar max |
Övning 2.3:8
| Se lösningen i webmaterialet när du loggat in till kursen. |
Övning 2.3:9
| a) | $(-1,0)\ $ och $\ (1,0)$ | b) | $(2,0)\ $ och $\ (3,0)$ | c) | $(1,0)\ $ och $\ (3,0)$ |
Övning 2.3:10
| Se lösningen i webmaterialet när du loggat in till kursen |