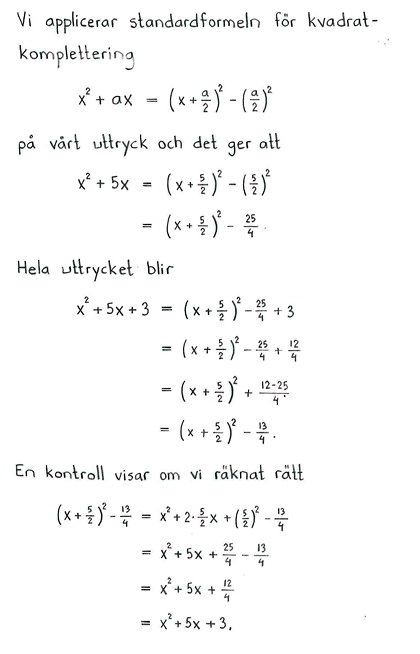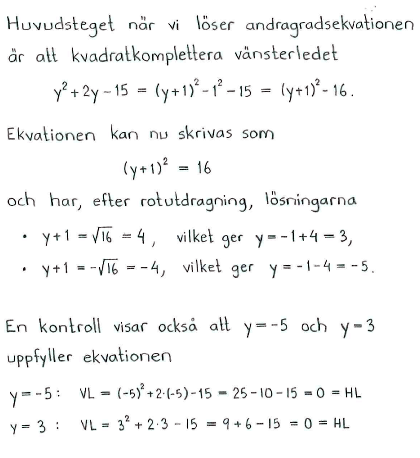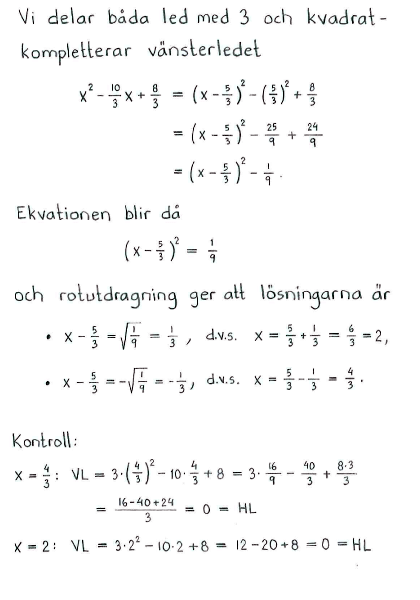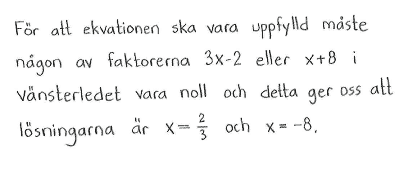Övn 2.3
Sommarmatte 1
Innehåll |
Övning 2.3:1
Kvadratkomplettera följande uttryck
| a) | $x^2-2x$ | b) | $x^2+2x-1$ | c) | $5+2x-x^2$ | d) | $x^2+5x+3$ |
| a) | $(x-1)^2-1$ | b) | $(x+1)^2-2$ | c) | $-(x-1)^2+6$ | d) | $\bigl(x+\frac{5}{2}\bigr)^2-\frac{13}{4}$ |
</div>
Lösning till delfråga a)
|
|
Lösning till delfråga b)
|
|
Lösning till delfråga c)
|
|
Lösning till delfråga d)
|
|
Övning 2.3:2
Lös följande andragradsekvationer med kvadratkomplettering
| a) | $x^2-4x+3=0$ | b) | $y^2+2y-15=0$ | c) | $y^2+3y+4=0$ |
| d) | $4x^2-28x+13=0$ | e) | $5x^2+2x-3=0$ | f) | $3x^2-10x+8=0$ |
Facit till alla delfrågor
| a) | $\left\{ \eqalign{ x_1 &= 1 \cr x_2 &= 3\cr }\right.$ | b) | $\left\{ \eqalign{ y_1 &= -5 \cr y_2 &= 3\cr }\right.$ | c) | saknar (reella) lösning |
| d) | $ \left\{ \eqalign{ x_1 &= \textstyle\frac{1}{2}\cr x_2 &= \textstyle\frac{13}{2}\cr }\right.$ | e) | $\left\{ \eqalign{ x_1 &= -1 \cr x_2 &= \textstyle\frac{3}{5}\cr }\right.$ | f) | $ \left\{ \eqalign{ x_1 &= \textstyle\frac{4}{3}\cr x_2 &= 2\cr }\right.$ |
Lösning till delfråga a)
|
|
Lösning till delfråga b)
|
|
Lösning till delfråga c)
|
|
Lösning till delfråga d)
|
|
Lösning till delfråga e)
|
|
Lösning till delfråga f)
|
|
Övning 2.3:3
Lös följande ekvationer direkt
| a) | $x(x+3)=0$ | b) | $(x-3)(x+5)=0$ |
| c) | $5(3x-2)(x+8)=0$ | d) | $x(x+3)-x(2x-9)=0$ |
| e) | $(x+3)(x-1)-(x+3)(2x-9)=0$ | f) | $x(x^2-2x)+x(2-x)=0$ |
Facit till alla delfrågor
| a) | $\left\{ \eqalign{ x_1 &= 0 \cr x_2 & = -3\cr }\right.$ | b) | $\left\{ \eqalign{ x_1 &= 3 \cr x_2 & = -5\cr }\right. $ |
| c) | $\left\{ \eqalign{ x_1 & = \textstyle\frac{2}{3} \cr x_2 & = -8\cr }\right. $ | d) | $\left\{ \eqalign{ x_1 & = 0\cr x_2 & = 12\cr }\right. $ |
| e) | $\left\{ \eqalign{ x_1 & = -3 \cr x_2 & = 8\cr }\right. $ | f) | $\left\{ \eqalign{ x_1 & = 0 \cr x_2 & = 1 \cr x_3 & = 2 }\right. $ |
Lösning till delfråga a)
|
|
Lösning till delfråga b)
|
|
Lösning till delfråga c)
|
|
Lösning till delfråga d)
|
|
Lösning till delfråga e)
|
|
Lösning till delfråga f)
|
|
Övning 2.3:4
Bestäm en andragradsekvation som har rötterna
| a) | $-1\ $ och $\ 2$ |
| b) | $1+\sqrt{3}\ $ och $\ 1-\sqrt{3}$ |
| c) | $3\ $ och $\ \sqrt{3}$ |
Facit till alla delfrågor
| a) | $ax^2-ax-2a=0\,$, där $\,a\ne 0\,$ är en konstant. |
| b) | $ax^2-2ax-2a=0\,$, där $\,a\ne 0\,$ är en konstant. |
| c) | $ax^2-(3+\sqrt{3}\,)ax+3\sqrt{3}\,a=0\,$, där $\,a\ne 0\,$ är en konstant. |
Lösning till delfråga a)
|
|
|
|
Lösning till delfråga b)
|
|
|
|
Lösning till delfråga c)
|
|
Övning 2.3:5
| a) | Bestäm en andragradsekvation som bara har $\,-7\,$ som rot. |
| b) | Bestäm ett värde på $\,x\,$ som gör att uttrycket $\,4x^2-28x+48\,$ är negativt. |
| c) | Ekvationen $\,x^2+4x+b=0\,$ har en rot $\,x=1\,$. Bestäm värdet på konstanten $\,b\,$. |
Facit till alla delfrågor
| a) | Exempelvis $\ x^2+14x+49=0\,$. |
| b) | $3< x<4$ |
| c) | $b=-5$ |
Lösning till delfråga a)
|
|
Lösning till delfråga b)
|
|
Lösning till delfråga c)
|
|
Övning 2.3:6
Bestäm det minsta värde som följande polynom antar
| a) | $x^2-2x+1$ | b) | $x^2-4x+2$ | c) | $x^2-5x+7$ |
Facit till alla delfrågor
| a) | $0$ | b) | $-2$ | c) | $\displaystyle \frac{3}{4}$ |
Lösning till delfråga a)
|
|
Lösning till delfråga b)
|
|
Lösning till delfråga c)
|
|
Övning 2.3:7
Bestäm det största värde som följande polynom antar
| a) | $1-x^2$ | b) | $-x^2+3x-4$ | c) | $x^2+x+1$ |
Facit till alla delfrågor
| a) | $1$ | b) | $\displaystyle -\frac{7}{4}$ | c) | saknar max |
Lösning till delfråga a)
|
|
Lösning till delfråga b)
|
|
Lösning till delfråga c)
|
|
Övning 2.3:8
Skissera grafen till följande funktioner
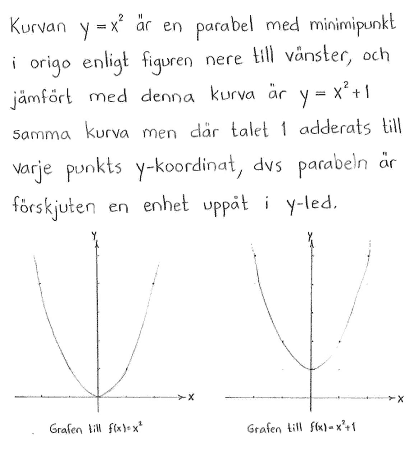
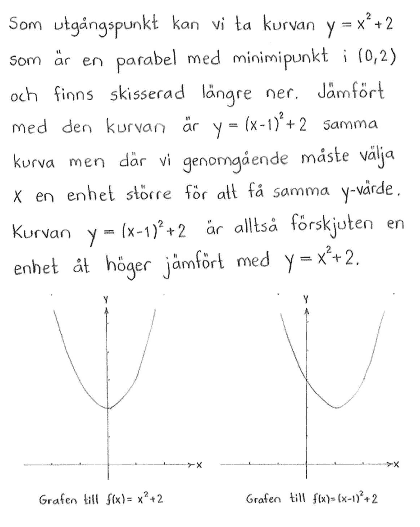
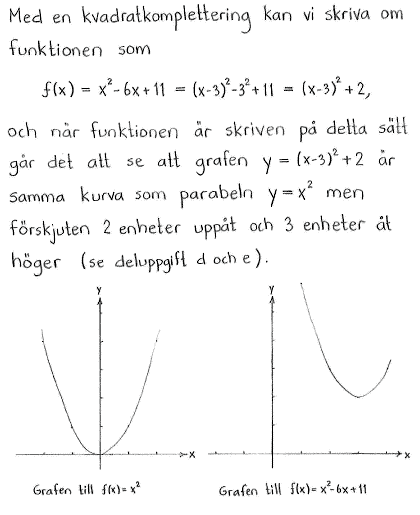
| a) | $f(x)=x^2+1$ | b) | $f(x)=(x-1)^2+2$ | c) | $f(x)=x^2-6x+11$ |
Facit till alla delfrågor
| Se lösningarna. |
Lösning till delfråga a)
|
|
Lösning till delfråga b)
|
|
Lösning till delfråga c)
|
|
Övning 2.3:9
Hitta alla skärningspunkter mellan x-axeln och kurvan
| a) | $y=x^2-1$ | b) | $y=x^2-5x+6$ | c) | $y=3x^2-12x+9$ |
Facit till alla delfrågor
| a) | $(-1,0)\ $ och $\ (1,0)$ | b) | $(2,0)\ $ och $\ (3,0)$ | c) | $(1,0)\ $ och $\ (3,0)$ |
Övning 2.3:10
Rita in i ett xy-plan alla punkter vars koordinater $\,(x,y)\,$ uppfyller
| a) | $y \geq x^2\ $ och $\ y \leq 1 $ | b) | $y \leq 1-x^2\ $ och $\ x \geq 2y-3 $ |
| c) | $1 \geq x \geq y^2 $ | d) | $x^2 \leq y \leq x $ |
Facit till alla delfrågor
| Se lösningarna. |
