Teori
Det finns en mängd trigonometriska samband, med vilka man kan översätta mellan sinus-, cosinus- och tangensvärden för en vinkel eller multiplar av en vinkel. Dessa brukar också kallas trigonometriska identiteter, eftersom de endast är olika sätt att beskriva ett och samma uttryck med hjälp av olika trigonometriska funktioner. Här kommer vi att beskriva några av dessa trigonometriska samband. Det finns många fler än vi kan behandla här. De flesta kan härledas utifrån den s k trigonometriska ettan och additionsformlerna (se nedan), vilka är viktiga att kunna utantill.
Trigonometriska ettan
Detta samband är det mest grundläggande, men är i själva verket ingenting annat än Pythagoras sats, tillämpad i enhetscirkeln. Den rätvinkliga triangeln till höger visar att
$$(\sin v)^2 + (\cos v)^2 = 1\,\mbox{,}$$
vilket brukar skrivas $\,\sin^2\!v + \cos^2\!v = 1\,$.
Symmetrier
Med hjälp av enhetscirkeln och spegling kan man tack vare de trigonometriska funktionernas symmetrier hitta en stor mängd samband mellan cosinus och sinus.
$$\eqalign{\cos (-v) &= \cos v\vphantom{\Bigl(}\cr \sin (-v) &= - \sin v\vphantom{\Bigl(}\cr \cos (\pi-v) &= - \cos v\vphantom{\Bigl(}\cr \sin (\pi-v) &= \sin v\vphantom{\Bigl(}\cr}\qquad\quad \eqalign{\cos \Bigl(\displaystyle \frac{\pi}{2} -v \Bigr) &= \sin v\cr \sin \Bigl(\displaystyle \frac{\pi}{2} -v \Bigr) &= \cos v\cr \cos \Bigl(v + \displaystyle \frac{\pi}{2} \Bigr) &= - \sin v\cr \sin \Bigl( v + \displaystyle \frac{\pi}{2} \Bigr) &= \cos v\cr}$$
Istället för att försöka lära sig alla dessa samband utantill kan det vara bättre att lära sig härleda dem i enhetscirkeln.
Spegling i x-axeln
|
|
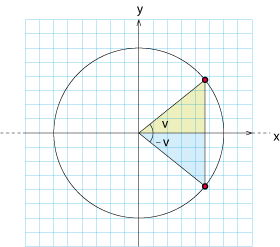
När en vinkel $\,v\,$ speglas i x-axeln blir den $\,-v\,$.
Speglingen påverkar inte x-koordinaten medan y-koordinaten byter tecken
$$\eqalign{\cos(-v) &= \cos v\,\mbox{,}\cr \sin (-v) &= - \sin v\,\mbox{.}\cr}$$
|
|
Spegling i y-axeln
|
|
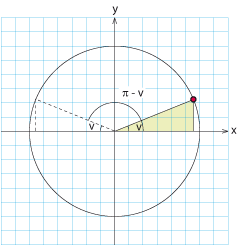
Vid spegling i y-axeln ändras vinkeln $\,v\,$ till $\,\pi-v\,$ (spegelbilden bildar vinkeln $\,v\,$ mot den negativa x-axeln).
Speglingen påverkar inte y-koordinaten medan x-koordinaten byter tecken
$$\eqalign{\cos(\pi-v) &= -\cos v\,\mbox{,}\cr \sin (\pi-v) &= \sin v\,\mbox{.}\cr}$$
|
|
Spegling i linjen y = x
|
|
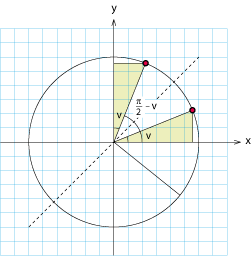
Vinkeln $\,v\,$ ändras till vinkeln $\,\pi/2 - v\,$ (spegelbilden bildar vinkeln $\,v\,$ mot den positiva y-axeln).
Speglingen gör att x- och y-koordinaterna byter plats
$$\eqalign{\cos \Bigl(\frac{\pi}{2} - v \Bigr) &= \sin v\,\mbox{.}\cr \sin \Bigl(\frac{\pi}{2} - v \Bigr) &= \cos v\,\mbox{.}\cr}$$
|
|
Vridning med vinkeln $\,\mathbf{\pi/2}\,$
|
|
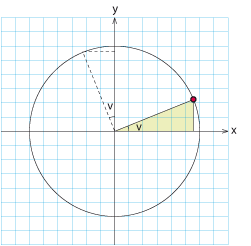
En vridning $\,\pi/2\,$ av vinkeln $\,v\,$ betyder att vinkeln blir $\,v+ \pi/2\,$.
Vridningen gör att x-koordinaten blir ny y-koordinat och y-koordinaten blir ny x-koordinat fast med omvänt tecken
$$\eqalign{\cos \Bigl(v+\frac{\pi}{2}\Bigr) &= -\sin v\,\mbox{,}\cr \sin \Bigl(v+\frac{\pi}{2} \Bigr) &= \cos v\,\mbox{.}}$$
|
|
Alternativt kan man få fram dessa samband genom att spegla och/eller förskjuta graferna. Om man exempelvis vill ha ett samband där $\,\cos v\,$ uttrycks med hjälp av sinus så kan man förskjuta grafen för cosinus så att den passar med sinuskurvan. Detta kan göras på flera olika sätt, men mest naturligt faller det sig att skriva $\,\cos v = \sin (v + \pi / 2)\,$. För att undvika misstag kan man kontrollera att det stämmer för några olika värden på $\,v\,$.
Kontroll: $\ \cos 0 = \sin (0 + \pi / 2)=0\,$.
Additions- och subtraktionsformlerna och formler för dubbla vinkeln
Ofta behöver man behandla uttryck där två eller flera vinklar är inblandade, t.ex. $\,\sin(u+v)\,$. Man behöver då de s.k. additionsformlerna. För sinus och cosinus har formlerna utseendet
$$\eqalign{\sin(u + v) &= \sin u\,\cos v + \cos u\,\sin v\,\mbox{,}\cr \sin(u – v) &= \sin u\,\cos v – \cos u\,\sin v\,\mbox{,}\cr \cos(u + v) &= \cos u\,\cos v – \sin u\,\sin v\,\mbox{,}\cr \cos(u – v) &= \cos u\,\cos v + \sin u\,\sin v\,\mbox{.}\cr}$$
Om man vill veta sinus eller cosinus för dubbla vinkeln, dvs $\,\sin 2v\,$ eller $\,\cos 2v\,$, så kan man skriva uttrycken som $\,\sin(v + v)\,$ eller $\,\cos(v + v)\,$ och använda additionsformlerna ovan och få
$$\eqalign{\sin 2v &= 2 \sin v \cos v\,\mbox{,}\cr \cos 2v &= \cos^2\!v – \sin^2\!v \,\mbox{.}\cr}$$
Ur dessa samband kan vi sedan få fram formler för halva vinkeln. Genom att byta ut $\,2v\,$ mot $\,v\,$, och följdaktligen $\,v\,$ mot $\,v/2\,$, i formeln för $\,\cos 2v\,$ får vi att
$$\cos v = \cos^2\!\frac{v}{2} – \sin^2\!\frac{v}{2}\,\mbox{.}$$
Vill vi ha en formel för $\,\sin(v/2)\,$ så använder vi därefter den trigonometriska ettan för att bli av med $\,\cos^2(v/2)$
$$\cos v = 1 – \sin^2\!\frac{v}{2}\, – \sin^2\!\frac{v}{2} = 1 – 2\sin^2\!\frac{v}{2}$$
dvs.
$$ \sin^2\!\frac{v}{2} = \frac{1 – \cos v}{2}\,\mbox{.}$$
På motsvarande sätt kan vi med den trigonometriska ettan göra oss av med $\,\sin^2(v/2)\,$. Då får vi istället
$$\cos^2\!\frac{v}{2}= \frac{1 + \cos v}{2}\,\mbox{.}$$
Tänk på att:
Enhetscirkeln är ett ovärderligt hjälpmedel för att hitta trigonometriska samband. Sådana finns det gott om och det är ingen idé att försöka lära sig alla utantill. Det är också tidsödande att behöva slå upp och leta fram dem hela tiden. Därför är det mycket bättre att du lär dig använda enhetscirkeln.
Den allra mest kända trigonometriska formeln är den s k trigonometriska ettan. Den gäller för alla vinklar, inte bara för spetsiga. Den hänger ihop med Pythagoras sats.
|