Exempel 1

Lös ekvationen $\sin x = 1/2$.

Lösning:

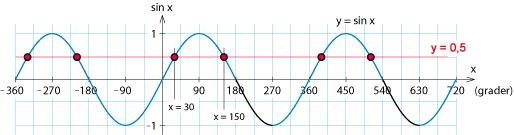
Vår uppgift är att bestämma alla vinklar som gör att sinus av vinkeln blir $1/2$. Vi tar hjälp av enhetscirkeln. Notera att vinklen här kallas $x$.

Bild: figur 3.5.1

I figuren har vi angivit de två riktningar som ger punkter med $y$-koordinat $1/2$ i enhetscirkeln, d.v.s. vinklar med sinusvärdet $\frac{1}{2}$. Den första är standardvinkeln $30^\circ = \pi / 6 $ och symmetriskäl bildar den andra vinkeln $30^\circ$ mot den negativa $x$-axeln, vilket gör at den vinkeln är $180^\circ – 30^\circ = 150^\circ$ eller i radianer $\pi – \pi / 6 = 5\pi / 6$. Detta är de enda lösningar till ekvationen $\sin x = \frac{1}{2}$ mellan $0$ och $2\pi$.

Vi kan dock lägga till ett godtyckligt antal varv till dessa två vinklar och fortfarande få samma sinusvärde. Alla vinklar med sinusvärde $\frac{1}{2}$ är alltså $$\left\{ \matrix{x=\displaystyle \frac{\pi}{6} + 2n\pi \\ x=\displaystyle \frac{5\pi}{6} + 2n\pi}\right.$$ där $n$ är ett godtyckligt heltal. Detta kallas den fullständiga lösningen till ekvationen.

Lösningarna syns också i figuren nedan där grafen till $y = \sin x$ skär linjen $y=\frac{1}{2}$.

Exempel 2

Lös ekvationen $\cos x = 1/2$.

Lösning:

Vi tar igen hjälp av enhetscirkeln.

<img src="object49972/bilder/3_5/3_5_03.gif">

Vi vet att cosinus blir 1/2 för vinkeln $\pi/3$. En annan vinkel som ger samma värde på cosinus är $-\pi/3$. Dessa två riktningar skall återkomma varje varv. Den fullständiga lösningen blir alltså $x = \pm \pi/3 + n \cdot 2\pi $, där n är ett godtyckligt heltal.

Exempel 3

Lös ekvationen $\tan x = \sqrt{3}$.

Lösning:

Först måste vi hitta en lösning. Vi kan rita upp en rätvinklig triangel, med vars hjälp vi bestämmer den första lösningen.

<img src="object49972/bilder/3_5/3_5_04.gif">

I vårt fall får vi $x = 60^\circ = \pi/3$. Sedan kan vi rita en figur för att illustrera var vi hittar resten av lösningarna.

<img src="object49972/bilder/3_5/3_5_05.gif">

Även här upprepar sig lösningarna för varje varv, men skillnaden mellan lösningarna är alltid ett halvt varv för tangens.

Den fullständiga lösningen blir $x = \pi/3 + n \cdot \pi$, där n är ett godtyckligt heltal.

Exempel 4

Lös ekvationen $4\cos 2x – \cos x = 0$.

Lösning:

Omskrivning med hjälp av formeln $\cos 2x = 2 \cos^2 x – 1$ ger

$4(2 \cos^2 x – 1) – \cos x = 0$

$8 \cos^2 x – 4 – \cos x = 0$

$\cos^2 x – \displaystyle\frac{1}{8}\cos x – \displaystyle\frac{1}{2} = 0$

$\cos x = \displaystyle\frac{1}{16} \pm \sqrt{ \left(\displaystyle\frac{1}{16}\right)^2 + \displaystyle\frac{1}{2}}$

Exempel 5

Lös ekvationen $\displaystyle\frac{1}{2}\sin x + 1 – \cos^2 x = 0$.

Lösning:

Enligt trigonometriska ettan är $\sin ^2 x + \cos^2 x = 1$, dvs $1 – \cos^2 x = \sin^2 x$.

Ekvationen kan alltså skrivas $\displaystyle\frac{1}{2}\sin x + \sin^2 x = 0$.

Genom att nu bryta ut en faktor $\sin x$ får vi $(\sin x )\left(\displaystyle\frac{1}{2} + \sin x\right) = 0$.

Ekvationen delas sedan upp i de två grundekvationerna: $\sin x = 0$ och $\sin x = -1/2$, vilka är vanliga ekvationer på formen $\sin x = a$, där a är ett tal, och där vi enkelt kan hitta den fullständiga lösningsmängden enligt exempel 1

Exempel 6

Lös ekvationen $\sin 2x =4 \cos x$.

Lösning:

Genom omskrivning med formeln för dubbla vinkeln blir ekvationen

$2\sin x \cos x – 4 \cos x = 0$.

Vi delar med 2 och bryter ut en faktor $\cos x$, vilket ger

$(\cos x)( \sin x – 2) = 0$.

Eftersom produkten bara kan bli noll genom att en faktor är noll, så kan ekvationen delas upp i grundekvationerna

$\cos x = 0$ och $\sin x = 2$.

Men $\sin x$ kan aldrig bli större än 1, så ekvationen $\sin x = 2$ saknar lösningar. Då återstår bara $\cos x = 0$, vilket med hjälp av enhetscirkeln ger den fullständiga lösningen $x = \pi / 2 + n \cdot \pi$.

Exempel 7

Lös ekvationen $4 \sin^2 x – 4 \cos x = 1$.

Lösning:

Med trigonometriska ettan kan $\sin^2 x$ bytas ut mot $1 – \cos^2 x$. Då får vi

$4 (1 – \cos^2 x) – 4 \cos x = 1$

$4 – 4 \cos^2 x – 4 \cos x = 1$

$– 4 \cos^2 x – 4 \cos x + 4 – 1 = 0$

$\cos^2 x + \cos x – 3/4 = 0$ Detta är en andragradsekvation i $\cos x$, som kan lösas med den så kallade pq-formeln.

$\cos x = - \displaystyle\frac{1}{2} \pm \sqrt{\left(\displaystyle\frac{1}{2}\right)^2 + \displaystyle\frac{3}{4}} = - \displaystyle\frac{1}{2} \pm \sqrt{\displaystyle\frac{1}{4} + \displaystyle\frac{3}{4}}= - \displaystyle\frac{1}{2} \pm 1 $

Eftersom värdet av $\cos x $ ligger mellan – 1 och 1 kan vi förkasta alla lösningar utanför detta intervall. Då återstår bara grundekvationen

$\cos x = 1/2$,

som löses enligt exempel 2.