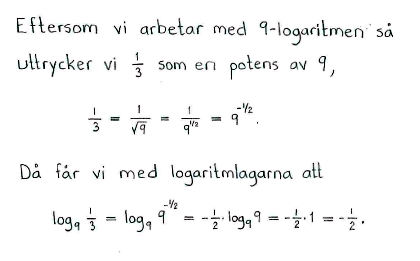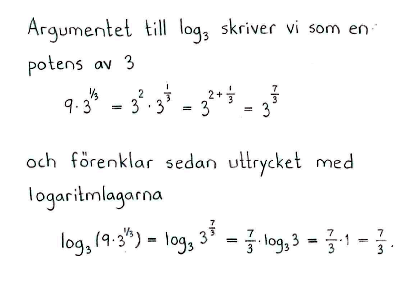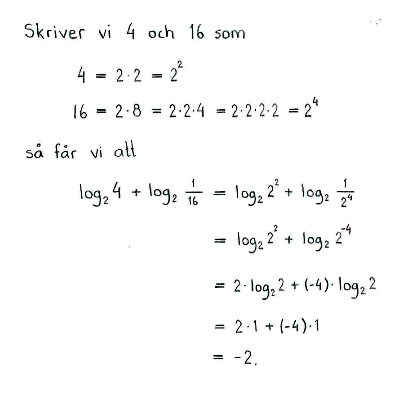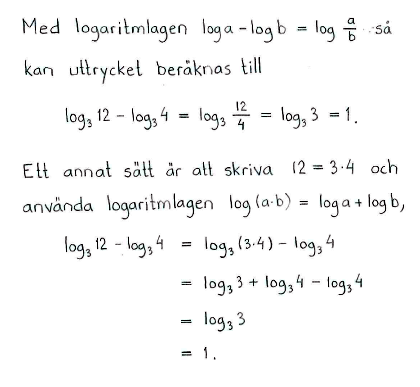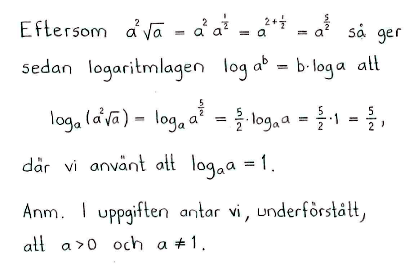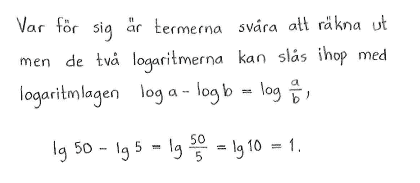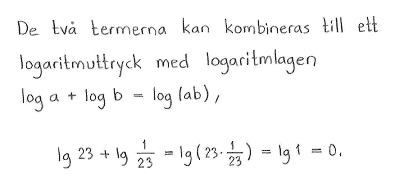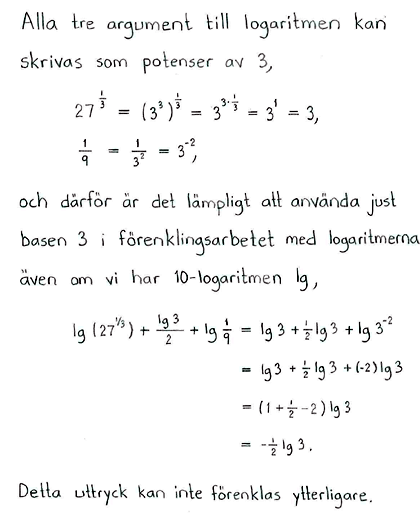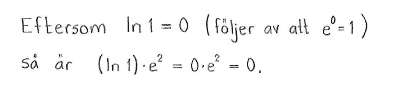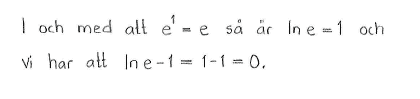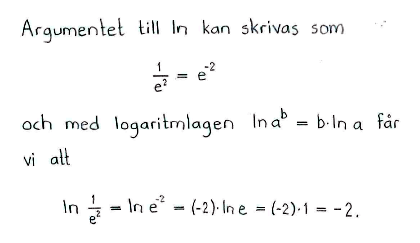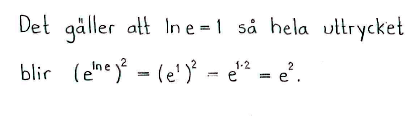Övn 3
Sommarmatte 1
Övning 3.1:1
Skriv i potensform
| a) | $\sqrt{2}$ | b) | $\sqrt{7^5}$ | c) | $\bigl(\sqrt[\scriptstyle3]{3}\,\bigr)^4$ | d) | $\sqrt{\sqrt{3}}$ |
| a) | $2^{1/2}$ | b) | $7^{5/2}$ | c) | $3^{4/3}$ | d) | $3^{1/4}$ |
Övning 3.1:2
Förenkla så långt som möjligt
| a) | $\sqrt{3^2}$ | b) | $\sqrt{\left(-3\right)^2}$ | c) | $\sqrt{-3^2}$ | d) | $\sqrt{5}\cdot\sqrt[\scriptstyle3]{5}\cdot5$ |
| e) | $\sqrt{18}\cdot\sqrt{8}$ | f) | $\sqrt[\scriptstyle3]{8}$ | g) | $\sqrt[\scriptstyle3]{-125}$ | ||
| a) | $3$ | b) | $3$ | c) | ej definierad | d) | $5^{11/6}$ |
| e) | $12$ | f) | $2$ | g) | $-5$ | ||
Övning 3.1:3
Förenkla så långt som möjligt
| a) | $\bigl(\sqrt{5}-\sqrt{2}\,\bigr)\bigl(\sqrt{5}+\sqrt{2}\,\bigr)$ | b) | $\displaystyle \frac{\sqrt{96}}{\sqrt{18}}$ |
| c) | $\sqrt{16+\sqrt{16}}$ | d) | $\sqrt{\displaystyle \frac{2}{3}}\bigl(\sqrt{6}-\sqrt{3}\,\bigr)$ |
| a) | $3$ | b) | $\displaystyle \frac{4\sqrt{3}}{3}$ |
| c) | $2\sqrt{5}$ | d) | $2-\sqrt{2}$ |
Övning 3.1:4
Förenkla så långt som möjligt
| a) | $\sqrt{0{,}16}$ | b) | $\sqrt[\scriptstyle3]{0{,}027}$ | |
| c) | $\sqrt{50}+4\sqrt{20}-3\sqrt{18}-2\sqrt{80}$ | d) | $\sqrt{48}+ \sqrt{12} +\sqrt{3} -\sqrt{75}$ | |
| a) | $0{,}4$ | b) | $0{,}3$ |
| c) | $-4\sqrt{2}$ | d) | $2\sqrt{3}$ |
Övning 3.1:5
Skriv som ett uttryck utan rottecken i nämnaren.
| a) | $\displaystyle \frac{2}{\sqrt{12}}$ | b) | $\displaystyle \frac{1}{\sqrt[\scriptstyle3]{7}}$ | c) | $\displaystyle \frac{2}{3+\sqrt{7}}$ | d) | $\displaystyle \frac{1}{\sqrt{17}-\sqrt{13}}$ |
| a) | $\displaystyle \frac{\sqrt{3}}{3}$ | b) | $\displaystyle \frac{7^{2/3}}{7}$ | c) | $3-\sqrt{7}$ | d) | $\displaystyle \frac{\sqrt{17}+\sqrt{13}}{4}$ |
Övning 3.1:6
Skriv som ett uttryck utan rottecken i nämnaren.
| a) | $\displaystyle \frac{\sqrt{2}+3}{\sqrt{5}-2}$ | b) | $\displaystyle \frac{1}{\left(\sqrt{3}-2\right)^2-2}$ |
| c) | $\displaystyle \frac{\displaystyle \frac{1}{\sqrt{3}}-\displaystyle \frac{1}{\sqrt{5}}}{\displaystyle \frac{1}{\sqrt{2}}-\displaystyle \frac{1}{2}}$ | d) | $\displaystyle \frac{1}{\sqrt{2}+\sqrt{3}+\sqrt{6}}$ |
| a) | $6+2\sqrt{2}+3\sqrt{5}+\sqrt{10}$ | b) | $-\displaystyle \frac{5+4\sqrt{3}}{23}$ |
| c) | $\displaystyle \frac{2}{3}\sqrt{6}+\displaystyle \frac{2}{3}\sqrt{3}-\displaystyle \frac{2}{5}\sqrt{10}-\displaystyle \frac{2}{5}\sqrt{5}$ | d) | $\displaystyle \frac{5\sqrt{3}+7\sqrt{2}-\sqrt{6}-12}{23}$ |
Övning 3.1:7
Förenkla så långt som möjligt
| a) | $\displaystyle \frac{1}{\sqrt{6}-\sqrt{5}} - \displaystyle \frac{1}{\sqrt{7}-\sqrt{6}}$ | b) | $\displaystyle \frac{5\sqrt{7}-7\sqrt{5}}{\sqrt{7}-\sqrt{5}}$ | c) | $\displaystyle \sqrt{153}-\sqrt{68}$ |
| a) | $\sqrt{5}-\sqrt{7}$ | b) | $-\sqrt{35}$ | c) | $\sqrt{17}$ |
Övning 3.1:8
Avgör vilket tal som är störst av
| a) | $\sqrt[\scriptstyle3]5\ $ och $\ \sqrt[\scriptstyle3]6$ | b) | $\sqrt7\ $ och $\ 7$ |
| c) | $\sqrt7\ $ och $\ 2{,}5$ | d) | $\sqrt2\bigl(\sqrt[\scriptstyle4]3\,\bigr)^3\ $ och $\ \sqrt[\scriptstyle3]2\cdot3$ |
| a) | $\sqrt[\scriptstyle3]6 > \sqrt[\scriptstyle3]5$ | b) | $7 > \sqrt7$ |
| c) | $\sqrt7 > 2{,}5$ | d) | $\sqrt[\scriptstyle3]2\cdot3 > \sqrt2\bigl(\sqrt[\scriptstyle4]3\,\bigr)^3$ |
Övning 3.2:1
| Lös ekvationen $\ \sqrt{x-4}=6-x\,$. |
| $x=5$ |
Övning 3.2:2
| Lös ekvationen $\ \sqrt{2x+7}=x+2\,$. |
| $x=1$ |
Övning 3.2:3
| Lös ekvationen $\ \sqrt{3x-8}+2=x\,$. |
| $\left \{ \eqalign{ x_1 & = 3 \cr x_2 & = 4\cr } \right.$ |
Övning 3.2:4
| Lös ekvationen $\ \sqrt{1-x}=2-x\,$. |
| Saknar lösning. |
Övning 3.2:5
| Lös ekvationen $\ \sqrt{3x-2}=2-x\,$. |
| $x=1$ |
Övning 3.2:6
| Lös ekvationen $\ \sqrt{x+1}+\sqrt{x+5}=4\,$. |
| $x=\displaystyle\frac{5}{4}$ |
Övning 3.3:1
Bestäm $\,x\,$ om
| a) | $10^x=1\,000$ | b) | $10^x=0{,}1$ |
| c) | $\displaystyle \frac{1}{10^x}=100$ | d) | $\displaystyle \frac{1}{10^x}=0{,}000\,1$ |
| a) | $x=3$ | b) | $x=-1$ |
| c) | $x=-2$ | d) | $x=4$ |
Övning 3.3:2
Beräkna
| a) | $\lg{ 0{,}1}$ | b) | $\lg{ 10\,000}$ | c) | $\lg {0{,}001}$ | d) | $\lg {1}$ |
| e) | $10^{\lg{2}}$ | f) | $\lg{10^3}$ | g) | $10^{-\lg{0{,}1}}$ | h) | $\lg{\displaystyle \frac{1}{10^2}}$ |
| a) | $-1$ | b) | $4$ | c) | $-3$ | d) | $0$ |
| e) | $2$ | f) | $3$ | g) | $10$ | h) | $-2$ |
Övning 3.3:3
Beräkna
| a) | $\log_2{8}$ | b) | $\log_9{\displaystyle \frac{1}{3}}$ | c) | $\log_2{0{,}125}$ |
| d) | $\log_3{\left(9\cdot3^{1/3}\right)}$ | e) | $2^{\log_{\scriptstyle2}{4}}$ | f) | $\log_2{4}+\log_2{\displaystyle \frac{1}{16}}$ |
| g) | $\log_3{12}-\log_3{4}$ | h) | $\log_a{\bigl(a^2\sqrt{a}\,\bigr)}$ | ||
Facit
Facit till alla delfrågor
| a) | $3$ | b) | $-\displaystyle \frac{1}{2}$ | c) | $-3$ |
| d) | $\displaystyle \frac{7}{3}$ | e) | $4$ | f) | $-2$ |
| g) | $1$ | h) | $\displaystyle \frac{5}{2}$ | ||
Lösning a)
Lösning till delfråga a)
|
|
Lösning b)
Lösning till delfråga b)
|
|
Lösning c)
Lösning till delfråga c)
|
|
Lösning d)
Lösning till delfråga d)
|
|
Lösning e)
Lösning till delfråga e)
|
|
Lösning f)
Lösning till delfråga f)
|
|
Lösning g)
Lösning till delfråga g)
|
|
Lösning h)
Lösning till delfråga h)
|
|
Övning 3.3:4
Förenkla
| a) | $\lg{50}-\lg{5}$ | b) | $\lg{23}+\lg{\displaystyle \frac{1}{23}}$ | c) | $\lg{27^{1/3}}+\displaystyle \frac{\lg{3}}{2}+\lg{\displaystyle \frac{1}{9}}$ |
Facit
Facit till alla delfrågor
| a) | $1$ | b) | $0$ | c) | $-\displaystyle \frac{1}{2}\lg{3}$ |
Lösning a)
Lösning till delfråga a)
|
|
Lösning b)
Lösning till delfråga b)
|
|
Lösning c)
Lösning till delfråga c)
|
|
Övning 3.3:5
Förenkla
| a) | $\ln{e^3}+\ln{e^2}$ | b) | $\ln{8}-\ln{4}-\ln{2}$ | c) | $(\ln{1})\cdot e^2$ |
| d) | $\ln{e}-1$ | e) | $\ln{\displaystyle \frac{1}{e^2}}$ | f) | $\left(e^{\ln{e}}\right)^2$ |
Facit
Facit till alla delfrågor
| a) | $5$ | b) | $0$ | c) | $0$ |
| d) | $0$ | e) | $-2$ | f) | $e^2$ |
Lösning a)
Lösning till delfråga a)
|
|
Lösning b)
Lösning till delfråga b)
|
|
Lösning c)
Lösning till delfråga c)
|
|
Lösning d)
Lösning till delfråga d)
|
|
Lösning e)
Lösning till delfråga e)
|
|
Lösning f)
Lösning till delfråga f)
|
|
Övning 3.3:6
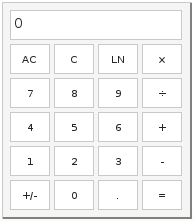
Använd miniräknaren till höger för att beräkna med tre decimaler (Knappen LN betecknar den naturliga logaritmen i basen e):
| a) | $\log_3{4}$ |
| b) | $\lg{46}$ |
| c) | $\log_3{\log_2{(3^{118})}}$ |
Facit
Facit till alla delfrågor
| a) | $1{,}262$ |
| b) | $1{,}663$ |
| c) | $4{,}762$ |
Lösning a)
Lösning till delfråga a)
|
|
|
|
Lösning b)
Lösning till delfråga b)
|
|
Lösning c)
Lösning till delfråga c)
|
|
|
|
