Sommarmatte 1
Övning 4.1:1
Skriv i grader och radianer
| a) |
$\displaystyle \frac{1}{4} \textrm{ varv} $ |
b) |
$\displaystyle \frac{3}{8} \textrm{ varv}$ |
| c) |
$-\displaystyle \frac{2}{3}\textrm{ varv}$ |
d) |
$\displaystyle \frac{97}{12} \textrm{ varv} $ |
|
| a) |
$90^\circ\ $ och $\ \displaystyle \frac{\pi}{2} \textrm{ rad} $ |
b) |
$135^\circ\ $ och $\ \displaystyle \frac{3\pi}{4} \textrm{ rad}$ |
| c) |
$-240^\circ\ $ och $\ \displaystyle -\frac{4\pi}{3} \textrm{ rad}$ |
d) |
$2910^\circ\ $ och $\ \displaystyle \frac{97\pi}{6} \textrm{ rad}$ |
|
Övning 4.1:2
Omvandla till radianer
| a) |
$45^\circ$ |
b) |
$135^\circ$ |
c) |
$-63^\circ$ |
d) |
$270^\circ$ |
|
| a) |
$\displaystyle \frac{\pi}{4}\textrm{ rad}$ |
b) |
$\displaystyle \frac{3\pi}{4}\textrm{ rad}$ |
c) |
$-\displaystyle \frac{7\pi}{20}\textrm{ rad}$ |
d) |
$\displaystyle \frac{3\pi}{2}\textrm{ rad}$ |
|
Övning 4.1:3
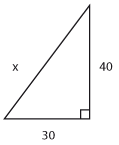
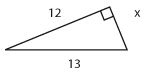
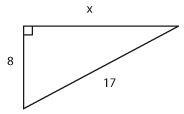
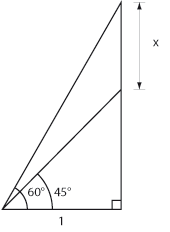
Bestäm längden av sidan som är markerad med $\,x$
| a) |
$x=50$ |
b) |
$x=5$ |
c) |
$x=15$ |
|
Övning 4.1:4
| a) |
Bestäm avståndet mellan punkterna (1,1) och (5,4). |
| b) |
Bestäm avståndet mellan punkterna (-2,5) och (3,-1). |
| c) |
Hitta den punkt på x-axeln som ligger lika långt från punkterna (3,3) och (5,1). |
|
| a) |
$5 \textrm{ l.e.}$ |
| b) |
$\sqrt{61} \textrm{ l.e.}$ |
| c) |
$(2,0)$ |
|
Övning 4.1:5
| a) |
Bestäm ekvationen för en cirkel med medelpunkt i (1,2) och radie 2. |
| b) |
Bestäm ekvationen för den cirkel som har medelpunkt i (2,-1) och innehåller punkten (-1,1). |
|
| a) |
$(x-1)^2+(y-2)^2=4$ |
| b) |
$(x-2)^2+(y+1)^2=13$ |
|
Övning 4.1:6
Skissera följande cirklar
| a) |
$x^2+y^2=9$ |
b) |
$(x-1)^2+(y-2)^2=3$ |
| c) |
$(3x-1)^2+(3y+7)^2=10$ |
|
| a) |
En cirkel med radie 3 och medelpunkt i origo. |
b) |
En cirkel med radie $\sqrt 3$ och medelpunkt i punkten (1, 2). |
| c) |
En cirkel med radie $\frac{1}{3}\sqrt 10$ och medelpunkt i punkten (1/3, -7/3). |
|
Övning 4.1:7
Skissera följande cirklar
| a) |
$x^2+2x+y^2-2y=1$ |
b) |
$x^2+y^2+4y=0$ |
| c) |
$x^2-2x+y^2+6y=-3$ |
d) |
$x^2-2x+y^2+2y=-2$ |
|
| "Se lösningen i webmaterialet när
du loggat in till kursen" |
|
Övning 4.1:8
Hur många varv snurrar ett hjul med radie 50 cm när det rullar 10m?
|
|
$\displaystyle \frac{10}{\pi}\textrm{ varv }\approx 3,2 \textrm{ varv} $ |
|
Övning 4.1:9
På en klocka är sekundvisaren 8 cm lång. Hur stor area sveper den över på 10 sekunder?
|
| $\displaystyle \frac{32\pi}{3} \textrm{ cm}^2 \approx 33,5 \textrm{ cm}^2$ |
|
Övning 4.1:10
En 5,4 m lång tvättlina hänger mellan två vertikala träd på 4,8 m avstånd från varandra. Linans ena ände är fäst 0,6 m högre än den andra änden, och 1,2 m från trädet där linan har sin lägre infästning hänger en kavaj på en galge. Bestäm hur mycket under den nedre infästningspunkten som galgen hänger (dvs. avståndet $\,x\,$ i figuren).
Övning 4.2:1
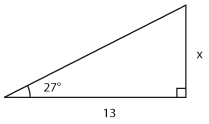
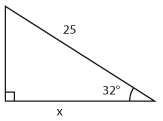
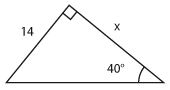
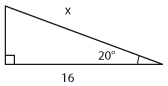
Bestäm längden av sidan som är markerad med $\,x\,$ uttryckt med hjälp av de trigonometriska funktionerna.
Facit till alla delfrågor
| a) |
$x=13\cdot\tan {27 ^\circ} \approx 6{,}62$ |
b) |
$x=25\cdot\cos {32 ^\circ} \approx 21{,}2$ |
| c) |
$x=\displaystyle\frac{14}{\tan {40 ^\circ}} \approx 16{,}7$ |
d) |
$x=\displaystyle\frac{16}{\cos {20 ^\circ}} \approx 17{,}0$ |
| e) |
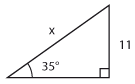
$x=\displaystyle\frac{11}{\sin {35 ^\circ}} \approx 19{,}2$ |
f) |
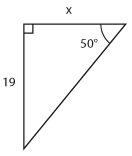
$x=\displaystyle\frac{19}{\tan {50 ^\circ}} \approx 15{,}9$ |
|
Övning 4.2:2
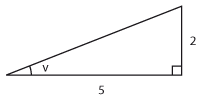
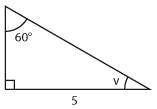
Bestäm en trigonometrisk ekvation som vinkeln $\,v\,$ uppfyller.
| a) |
$\tan v=\displaystyle\frac{2}{5}$ |
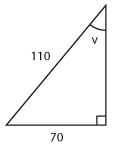
b) |
$\sin v=\displaystyle\frac{7}{11}$ |
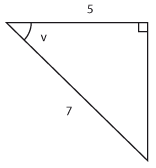
| c) |
$\cos v=\displaystyle\frac{5}{7}$ |
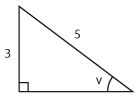
d) |
$\sin v=\displaystyle\frac{3}{5}$ |
| e) |
$v=30 ^\circ$ |
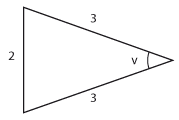
f) |
$\sin \displaystyle\frac{v}{2}=\displaystyle\frac{1}{3}$ |
|
Övning 4.2:3
Bestäm
| a) |
$\sin{\left(-\displaystyle \frac{\pi}{2}\right)}$ |
b) |
$\cos{2\pi}$ |
c) |
$\sin{9\pi}$ |
| d) |
$\cos{\displaystyle \frac{7\pi}{2}}$ |
e) |
$\sin{\displaystyle \frac{3\pi}{4}}$ |
f) |
$\cos{\left(-\displaystyle \frac{\pi}{6}\right)}$ |
|
| a) |
$-1$ |
b) |
$1$ |
c) |
$0$ |
| d) |
$0$ |
e) |
$\displaystyle \frac{1}{\sqrt{2}}$ |
f) |
$\displaystyle \frac{\sqrt{3}}{2}$ |
|
Övning 4.2:4
Bestäm
| a) |
$\cos{\displaystyle \frac{11\pi}{6}}$ |
b) |
$\cos{\displaystyle \frac{11\pi}{3}}$ |
c) |
$\tan{\displaystyle \frac{3\pi}{4}}$ |
| d) |
$\tan{\pi}$ |
e) |
$\tan{\displaystyle \frac{7\pi}{6}}$ |
f) |
$\tan{\left(-\displaystyle \frac{5\pi}{3}\right)}$ |
|
| a) |
$\displaystyle \frac{\sqrt{3}}{2}$ |
b) |
$\displaystyle \frac{1}{2}$ |
c) |
$-1$ |
| d) |
$0$ |
e) |
$\displaystyle \frac{1}{\sqrt{3}}$ |
f) |
$\sqrt{3}$ |
|
Övning 4.2:5
Bestäm
| a) |
$\cos{135^\circ}$ |
b) |
$\tan{225^\circ}$ |
c) |
$\cos{330^\circ}$ |
d) |
$\tan{495^\circ}$ |
|
| a) |
$-\displaystyle \frac{1}{\sqrt{2}}$ |
b) |
$1$ |
c) |
$\displaystyle \frac{\sqrt{3}}{2}$ |
d) |
$-1$ |
|
Övning 4.2:6
Bestäm längden av sidan som är markerad med $\,x\,$.
Övning 4.2:7
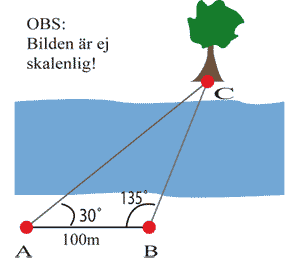
För att mäta upp bredden av en älv mäter vi från två punkter A och B längs den ena raka stranden vinkeln till ett träd C på motsatt sida älven. Hur bred är älven om måtten i figuren gäller?
| Älvens bredd är $\ \displaystyle\frac{100}{\sqrt{3}-1}$ m $\approx 136{,}6$ m. |
|
Övning 4.2:8
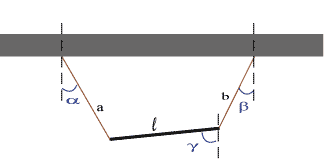
En stång med längd $\,\ell\,$ är upphängd i två linor med längd $\,a\,$ resp. $\,b\,$ enligt figuren. Linorna bildar vinklar $\,\alpha\,$ resp. $\,\beta\,$ med vertikalen. Bestäm en trigonometrisk ekvation för vinkeln $\,\gamma\,$ som stången bildar med vertikalen.
| $\ell\cos \gamma=a \cos \alpha - b\cos \beta $ |
|
Övning 4.2:9
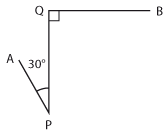
Bilvägen från A till B består av tre rätlinjiga delar AP, PQ och QB, vilka är 4,0 km, 12,0 km respektive 5,0 km. De i figuren markerade vinklarna vid P och Q är 30° respektive 90°. Beräkna avståndet fågelvägen från A till B. (Uppgiften är hämtad ur Centrala provet i matematik, november 1976, men aningen modifierad.)
| Avståndet är $\ \sqrt{205-48\sqrt{3}} \approx 11{,}0$ km. |
|
Övning 4.3:1
Bestäm de vinklar $\,v\,$ mellan $\,\displaystyle \frac{\pi}{2}\,$ och $\,2\pi\,$ som uppfyller
| a) |
$\cos{v}=\cos{\displaystyle \frac{\pi}{5}}$ |
b) |
$\sin{v}=\sin{\displaystyle \frac{\pi}{7}}$ |
c) |
$\tan{v}=\tan{\displaystyle \frac{2\pi}{7}}$ |
| a) |
$v = \displaystyle \frac{9\pi}{5}$ |
b) |
$v = \displaystyle \frac{6\pi}{7}$ |
c) |
$v = \displaystyle \frac{9\pi}{7}$ |
Övning 4.3:2
Bestäm de vinklar $\,v\,$ mellan 0 och $\,\pi\,$ som uppfyller
| a) |
$\cos{v} = \cos{\displaystyle \frac{3\pi}{2}}$ |
b) |
$\cos{v} = \cos{ \displaystyle \frac{7\pi}{5}}$ |
|
| a) |
$v=\displaystyle \frac{\pi}{2}$ |
b) |
$v=\displaystyle \frac{3\pi}{5}$ |
|
Övning 4.3:3
Antag att $\,-\displaystyle \frac{\pi}{2} \leq v \leq \displaystyle \frac{\pi}{2}\,$ och att $\,\sin{v} = a\,$. Uttryck med hjälp av $\,a$
| a) |
$\sin{(-v)}$ |
b) |
$\sin{(\pi-v)}$ |
| c) |
$\cos{v}$ |
d) |
$\sin{\left(\displaystyle \frac{\pi}{2}-v\right)}$ |
| e) |
$\cos{\left( \displaystyle \frac{\pi}{2} + v\right)}$ |
f) |
$\sin{\left( \displaystyle \frac{\pi}{3} + v \right)}$ |
|
| a) |
$-a$ |
b) |
$a$ |
| c) |
$\sqrt{1-a^2}$ |
d) |
$\sqrt{1-a^2}$ |
| e) |
$-a$ |
f) |
$\displaystyle \frac{\sqrt{3}}{2}\sqrt{1-a^2}+\displaystyle \frac{1}{2}\cdot a $ |
|
Övning 4.3:4
Antag att $\,0 \leq v \leq \pi\,$ och att $\,\cos{v}=b\,$. Uttryck med hjälp av $\,b\,$
| a) |
$\sin^2{v}$ |
b) |
$\sin{v}$ |
| c) |
$\sin{2v}$ |
d) |
$\cos{2v}$ |
| e) |
$\sin{\left( v+\displaystyle \frac{\pi}{4} \right)}$ |
f) |
$\cos{\left( v-\displaystyle \frac{\pi}{3} \right)}$ |
|
| a) |
$1-b^2$ |
b) |
$\sqrt{1-b^2}$ |
| c) |
$2b\sqrt{1-b^2}$ |
d) |
$2b^2-1$ |
| e) |
$\sqrt{1-b^2}\cdot\displaystyle \frac{1}{\sqrt{2}} + b\cdot \displaystyle \frac{1}{\sqrt{2}} $ |
f) |
$b\cdot\displaystyle \frac{1}{2}+\sqrt{1-b^2}\cdot\displaystyle \frac{\sqrt{3}}{2}$ |
|
Övning 4.3:5
För en spetsig vinkel $\,v\,$ i en triangel gäller att $\,\sin{v}=\displaystyle \frac{5}{7}\,$. Bestäm $\,\cos{v}\,$ och $\,\tan{v}\,$.
| $\cos{v}=\displaystyle \frac{2\sqrt{6}}{7}\quad$ och $\quad\tan{v}=\displaystyle \frac{5}{2\sqrt{6}}\,$. |
|
Övning 4.3:6
| a) |
Bestäm $\ \sin{v}\ $ och $\ \tan{v}\ $ om $\ \cos{v}=\displaystyle \frac{3}{4}\ $ och $\ \displaystyle \frac{3\pi}{2} \leq v \leq 2\pi\,$. |
| b) |
Bestäm $\ \cos{v}\ $ och $\ \tan{v}\ $ om $\ \sin{v}=\displaystyle \frac{3}{10}\ $ och $\,v\,$ ligger i den andra kvadranten. |
| c) |
Bestäm $\ \sin{v}\ $ och $\ \cos{v}\ $ om $\ \tan{v}=3\ $ och $\ \pi \leq v \leq \displaystyle \frac{3\pi}{2}\,$. |
|
| a) |
$\sin{v}=-\displaystyle \frac{\sqrt{7}}{4}\quad$ och $\quad\tan{v}=-\displaystyle \frac{\sqrt{7}}{3}\,$. |
|
| b) |
$\cos{v}=-\displaystyle \frac{\sqrt{91}}{10}\quad$ och $\quad\tan{v}=-\displaystyle \frac{3}{\sqrt{91}}\,$. |
|
| c) |
$\sin{v}=-\displaystyle \frac{3}{\sqrt{10}}\quad$ och $\quad\cos{v}=-\displaystyle \frac{1}{\sqrt{10}}\,$. |
|
Övning 4.3:7
Bestäm $\ \sin{(x+y)}\ $ om
| a) |
$\sin{x}=\displaystyle \frac{2}{3}\,$, $\ \sin{y}=\displaystyle \frac{1}{3}\ $ och $\,x\,$, $\,y\,$ är vinklar i första kvadranten. |
| b) |
$\cos{x}=\displaystyle \frac{2}{5}\,$, $\ \cos{y}=\displaystyle \frac{3}{5}\ $ och $\,x\,$, $\,y\,$ är vinklar i första kvadranten. |
|
| a) |
$\sin{(x+y)}=\displaystyle \frac{4\sqrt{2}+\sqrt{5}}{9}$ |
| b) |
$\sin{(x+y)}=\displaystyle \frac{3\sqrt{21}+8}{25}$ |
|
Övning 4.3:8
Visa följande trigonometriska samband
| a) |
$\tan^2v=\displaystyle\frac{\sin^2v}{1-\sin^2v}$ |
| b) |
$\displaystyle \frac{1}{\cos v}-\tan v=\frac{\cos v}{1+\sin v}$ |
| c) |
$\tan\displaystyle\frac{u}{2}=\frac{\sin u}{1+\cos u}$ |
| d) |
$\displaystyle\frac{\cos (u+v)}{\cos u \cos v}= 1- \tan u \tan v$ |
Övning 4.3:9
|
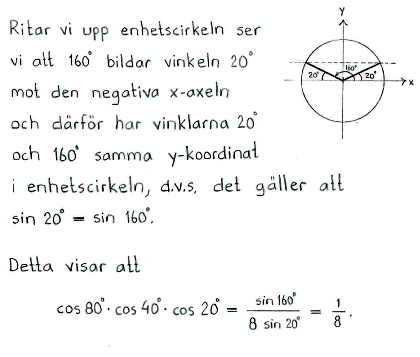
Visa "Feynmans likhet"
$$\cos 20^\circ \cdot \cos 40^\circ \cdot \cos 80^\circ = \displaystyle\frac{1}{8}\,\mbox{.}$$
(Ledtråd: Använd formeln för dubbla vinkeln på $\,\sin 160^\circ\,$.)
|
Övning 4.4:1
För vilka vinklar $\,v\,$, där $\,0 \leq v\leq 2\pi\,$, gäller att
| a) |
$\sin{v}=\displaystyle \frac{1}{2}$ |
b) |
$\cos{v}=\displaystyle \frac{1}{2}$ |
| c) |
$\sin{v}=1$ |
d) |
$\tan{v}=1$ |
| e) |
$\cos{v}=2$ |
f) |
$\sin{v}=-\displaystyle \frac{1}{2}$ |
| g) |
$\tan{v}=-\displaystyle \frac{1}{\sqrt{3}}$ |
|
| a) |
$\displaystyle v=\frac{\pi}{6}\,$, $\,\displaystyle v=\frac{5\pi}{6}$ |
b) |
$\displaystyle v=\frac{\pi}{3}\,$, $\,\displaystyle v=\frac{5\pi}{3}$ |
| c) |
$\displaystyle v=\frac{\pi}{2}$ |
d) |
$\displaystyle v=\frac{\pi}{4}\,$, $\,\displaystyle v=\frac{5\pi}{4}$ |
| e) |
lösning saknas |
f) |
$\displaystyle v=\frac{11\pi}{6}\,$, $\,\displaystyle v=\frac{7\pi}{6}$ |
| g) |
$\displaystyle v=\frac{5\pi}{6}\,$, $\,\displaystyle v=\frac{11\pi}{6}$ |
|
Övning 4.4:2
Lös ekvationen
| a) |
$\sin{x}=\displaystyle \frac{\sqrt{3}}{2}$ |
b) |
$\cos{x}=\displaystyle \frac{1}{2} $ |
c) |
$\sin{x}=0$ |
| d) |
$\sin{5x}=\displaystyle \frac{1}{\sqrt{2}} $ |
e) |
$\sin{5x}=\displaystyle \frac{1}{2}$ |
f) |
$\cos{3x}=-\displaystyle\frac{1}{\sqrt{2}}$ |
|
| a) |
$\left\{\eqalign{
x&=\displaystyle\frac{\pi}{3}+2n\pi\cr
x&=\displaystyle\frac{2\pi}{3}+2n\pi } \right.$
|
b) |
$\left\{\eqalign{
x&=\displaystyle\frac{\pi}{3}+2n\pi\cr
x&=\displaystyle\frac{5\pi}{3}+2n\pi } \right.$
|
c) |
$x=n\pi$ |
| d) |
$\left\{\eqalign{
x&=\displaystyle\frac{\pi}{20}+\displaystyle\frac{2n\pi}{5}\cr
x&=\displaystyle\frac{3\pi}{20}+\displaystyle\frac{2n\pi}{5} } \right.$
|
e) |
$\left\{\eqalign{
x&=\displaystyle\frac{\pi}{30}+\displaystyle\frac{2n\pi}{5}\cr
x&=\displaystyle\frac{\pi}{6}+\displaystyle\frac{2n\pi}{5}} \right.$
|
f) |
$\left\{\eqalign{
x&=\displaystyle\frac{\pi}{4}+\displaystyle\frac{2n\pi}{3}\cr
x&=\displaystyle\frac{5\pi}{12}+\displaystyle\frac{2n\pi}{3}} \right.$
|
|
Övning 4.4:3
Lös ekvationen
| a) |
$\cos{x}=\cos{\displaystyle \frac{\pi}{6}}$ |
b) |
$\sin{x}=\sin{\displaystyle \frac{\pi}{5}}$ |
| c) |
$\sin{(x+40^\circ)}=\sin{65^\circ}$ |
d) |
$\sin{3x}=\sin{15^\circ}$ |
|
| a) |
$\left\{\eqalign{
x&=\displaystyle\frac{\pi}{6}+2n\pi\cr
x&=\displaystyle\frac{11\pi}{6}+2n\pi
}\right.$
|
b) |
$\left\{\eqalign{
x&=\displaystyle\frac{\pi}{5}+2n\pi\cr
x&=\displaystyle\frac{4\pi}{5}+2n\pi
}\right.$
|
| c) |
$\left\{\eqalign{
x&=25^\circ + n\cdot 360^\circ\cr
x&=75^\circ + n\cdot 360^\circ
}\right.$
|
d) |
$\left\{\eqalign{
x&=5^\circ + n \cdot 120^\circ \cr
x&= 55^\circ + n \cdot 120^\circ
}\right.$
|
|
Övning 4.4:4
Bestäm de vinklar $\,v\,$ i intervallet $\,0^\circ \leq v \leq 360^\circ\,$ som uppfyller $\ \cos{\left(2v+10^\circ\right)}=\cos{110^\circ}\,$.
|
$v_1=50^\circ$, $\ \ v_2=120^\circ$, $\ \ v_3=230^\circ\ \ $ och $\ \ v_4=300^\circ$
|
Övning 4.4:5
Lös ekvationen
| a) |
$\sin{3x}=\sin{x}$ |
b) |
$\tan{x}=\tan{4x}$ |
| c) |
$\cos{5x}=\cos(x+\pi/5)$ |
|
| a) |
$\left\{\eqalign{
x&=n\pi\cr
x&=\displaystyle \frac{\pi}{4}+\displaystyle \frac{n\pi}{2}
}\right.$
|
b) |
$x=\displaystyle \frac{n\pi}{3}$ |
| c) |
$\left\{\eqalign{
x&=\displaystyle \frac{\pi}{20}+\displaystyle \frac{n\pi}{2}\cr
x&=-\displaystyle \frac{\pi}{30}+\displaystyle \frac{n\pi}{3}
}\right.$
|
|
Övning 4.4:6
Lös ekvationen
| a) |
$\sin x\cdot \cos 3x = 2\sin x$ |
b) |
$\sqrt{2}\sin{x}\cos{x}=\cos{x}$ |
| c) |
$\sin 2x = -\sin x$ |
|
| a) |
$x=n\pi$
|
b) |
$\left\{\eqalign{
x&=\displaystyle \frac{\pi}{4}+2n\pi\cr
x&=\displaystyle \frac{\pi}{2}+n\pi\cr
x&=\displaystyle \frac{3\pi}{4}+2n\pi}\right.$
|
| c) |
$\left\{\eqalign{
x&=\displaystyle \frac{2n\pi}{3}\cr
x&=\displaystyle \pi + 2n\pi\cr
}\right.$
|
|
Övning 4.4:7
Lös ekvationen
| a) |
$2\sin^2{x}+\sin{x}=1$ |
b) |
$2\sin^2{x}-3\cos{x}=0$ |
| c) |
$\cos{3x}=\sin{4x}$ |
|
| a) |
$\left\{ \matrix{
x=\displaystyle \frac{\pi}{6}+2n\pi\cr
x=\displaystyle \frac{5\pi}{6}+2n\pi\cr
x=\displaystyle \frac{3\pi}{2}+2n\pi
}\right.$
|
b) |
$x=\pm \displaystyle \frac{\pi}{3} + 2n\pi $ |
| c) |
$\left\{ \matrix{
x=\displaystyle \frac{\pi}{2}+2n\pi\cr
x=\displaystyle \frac{\pi}{14}+\displaystyle \frac{2n\pi}{7}
}\right.$
|
|
Övning 4.4:8
Lös ekvationen
| a) |
$\sin{2x}=\sqrt{2}\cos{x}$ |
b) |
$\sin{x}=\sqrt{3}\cos{x}$ |
| c) |
$\displaystyle \frac{1}{\cos^2{x}}=1-\tan{x}$ |
|
| a) |
$\left\{\eqalign{
x&=\displaystyle \frac{\pi}{4}+2n\pi\cr
x&=\displaystyle \frac{\pi}{2}+n\pi\cr
x&=\displaystyle \frac{3\pi}{4}+2n\pi
}\right.$
|
b) |
$x=\displaystyle \frac{\pi}{3}+n\pi$ |
| c) |
$\left\{\eqalign{
x&=n\pi\cr
x&=\displaystyle \frac{3\pi}{4}+n\pi
}\right.$
|
|