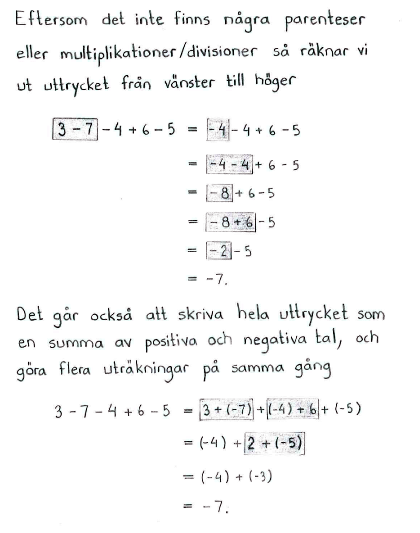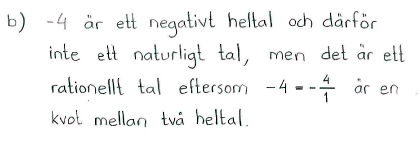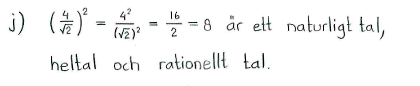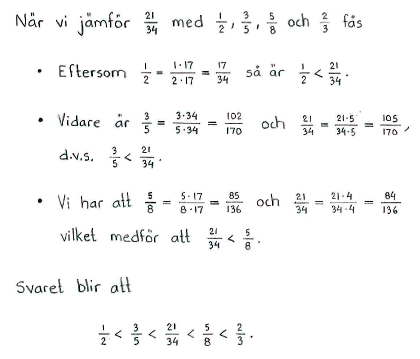1.1 Övningar
Sommarmatte 1
Innehåll |
Övning 1.1:1
Beräkna (utan hjälp av räknedosa)
| $\textrm{a) }$ | $3-7-4+6-5$ | $\textrm{b) }$ | $3-(7-4)+(6-5)$ |
| $\textrm{c) }$ | $3-(7-(4+6)-5)$ | $\textrm{d) }$ | $3-(7-(4+6))-5$ |
Facit till alla delfrågorna
| $\textrm{a)}$ | $-7$ | $\textrm{b)}$ | $1$ |
| $\textrm{c)}$ | $11$ | $\textrm{d)}$ | $1$ |
Lösning till delfråga a 
Lösning till delfråga b 
Lösning till delfråga c 
Lösning till delfråga d 
Övning 1.1:2
Beräkna (utan hjälp av räknedosa)
| $\textrm{a) }$ | $(3-(7-4))(6-5)$ | $\textrm{b) }$ | $3-(((7-4)+6)-5)$ |
| $\textrm{c) }$ | $3\cdot(-7)-4\cdot(6-5)$ | $\textrm{d) }$ | $3\cdot(-7)-(4+6)/(-5)$ |
Facit till alla delfrågorna
| $\textrm{a)}$ | $0$ | $\textrm{b)}$ | $-1$ |
| $\textrm{c)}$ | $-25$ | $\textrm{d)}$ | $-19$ |
Lösning till delfråga a 
Lösning till delfråga b 
Lösning till delfråga c 
Lösning till delfråga d 
Övning 1.1:3
Vilka av följande tal tillhör de naturliga talen? heltalen? rationella talen? irrationella talen? Förenkla först!
| $\textrm{a)}$ | $8$ | $\textrm{b)}$ | $-4$ | $\textrm{c)}$ | $8-4$ |
| $\textrm{d)}$ | $4-8$ | $\textrm{e)}$ | $8(-4)$ | $\textrm{f)}$ | $(-8)(-4)$ |
| $\textrm{g)}$ | $\displaystyle \frac{4}{-8}$ | $\textrm{h)}$ | $\displaystyle \frac{-8}{-4}$ | $\textrm{i)}$ | $\displaystyle \frac{\sqrt{2}}{3}$ |
| $\textrm{j)}$ | $\displaystyle \Bigl(\frac{4}{\sqrt{2}}\Bigr)^2$ | $\textrm{k)}$ | $-\pi$ | $\textrm{l)}$ | $\pi+1$ |
Facit till alla delfrågorna
| $\textrm{a)}$ | naturliga talen, heltalen, rationella talen | $\textrm{b)}$ | heltalen, rationella talen | $\textrm{c)}$ | naturliga talen, heltalen, rationella talen |
| $\textrm{d)}$ | heltalen, rationella talen | $\textrm{e)}$ | heltalen, rationella talen | $\textrm{f)}$ | naturliga talen, heltalen, rationella talen, |
| $\textrm{g)}$ | rationella talen | $\textrm{h)}$ | naturliga talen, heltalen, rationella talen | $\textrm{i)}$ | irrationella talen |
| $\textrm{j)}$ | naturliga talen, heltalen, rationella talen | $\textrm{k)}$ | irrationella talen | $\textrm{l)}$ | irrationella talen |
Lösning till delfråga a 
Lösning till delfråga b 
Lösning till delfråga c 
Lösning till delfråga d 
Lösning till delfråga e 
Lösning till delfråga f 
Lösning till delfråga g 
Lösning till delfråga h 
Lösning till delfråga i 
Lösning till delfråga j 
Lösning till delfråga k 
Lösning till delfråga l 
Övning 1.1:4
Ordna följande tal i storleksordning
| $\textrm{a)}$ | $\displaystyle 2,\ \frac{3}{5},\ \frac{5}{3}\ $ och $\ \displaystyle \frac{7}{3}$ | $\textrm{b)}$ | $\displaystyle -\frac{1}{2},\ -\frac{1}{5},\ -\frac{3}{10}\ $ och $\displaystyle -\frac{1}{3}$ | $\textrm{c)}$ | $\displaystyle \frac{1}{2},\ \frac{2}{3},\ \frac{3}{5},\ \frac{5}{8}$ och $\displaystyle \frac{21}{34}$ |
Facit till alla delfrågorna
| $\textrm{a)}$ | $\displaystyle \frac{3}{5}<\frac{5}{3}<2<\frac{7}{3}$ |
| $\textrm{b)}$ | $\displaystyle -\frac{1}{2}<-\frac{1}{3}<-\frac{3}{10}<-\frac{1}{5}$ |
| $\textrm{c)}$ | $\displaystyle \frac{1}{2}<\frac{3}{5}<\frac{21}{34}<\frac{5}{8}<\frac{2}{3}$ |
Lösning till delfråga a 
Lösning till delfråga b 
Lösning till delfråga c 
Övning 1.1:5
Ange decimalutvecklingen med tre korrekta decimaler till
| $\textrm{a)}$ | $\displaystyle \frac{7}{6}$ | $\textrm{b)}$ | $\displaystyle \frac{9}{4}$ | $\textrm{c)}$ | $\displaystyle \frac{2}{7}$ | $\textrm{d)}$ | $\sqrt{2}$ |
Facit till alla delfrågorna
| $\textrm{a)}$ | $1,167$ | $\textrm{b)}$ | $2,250$ | $\textrm{c)}$ | $0,286$ | $\textrm{d)}$ | $1,414$ |
Lösning till delfråga a 
Lösning till delfråga b 
Lösning till delfråga c 
Lösning till delfråga d 
Övning 1.1:6
Vilka av följande tal är rationella? Ange dem som en kvot mellan heltal.
| $\textrm{a)}$ | $3,14$ |
| $\textrm{b)}$ | $3,1416\,1416\,1416\dots$ |
| $\textrm{c)}$ | $0,2\,001\,001\,001\dots$(därefter är var tredje decimal en 1:a och övriga 0) |
| $\textrm{d)}$ | $0,\,10\,100\,1000\,10000\,1\dots$(en 1:1, en 0:a, en 1:a, två 0:or, 1n 1:a, tre 0:or osv) |
Facit till alla delfrågorna
| $\textrm{a)}$ | Talet är rationellt och lika med 314/100 = 157/50. |
| $\textrm{b)}$ | Talet är rationellt och är lika med 31413/9999 = 10471/3333 |
| $\textrm{c)}$ | Talet är rationellt och lika med 1999/9990 |
| $\textrm{d)}$ | Talet är irrationellt |
Lösning till delfråga a 
Lösning till delfråga b 
Lösning till delfråga c
Bild:1 1 6c.gif
Lösning till delfråga d 
