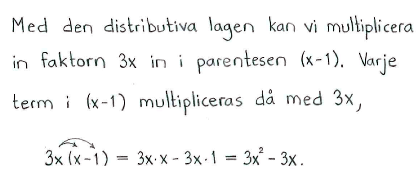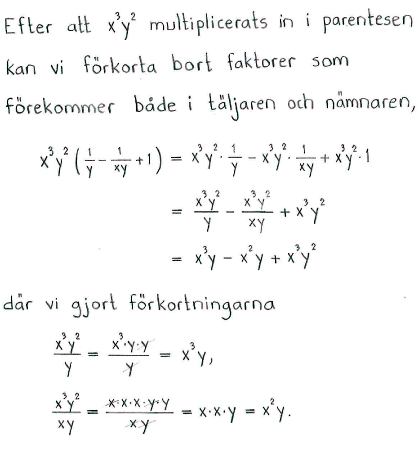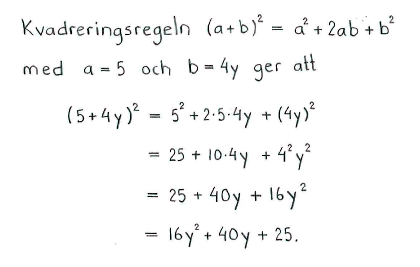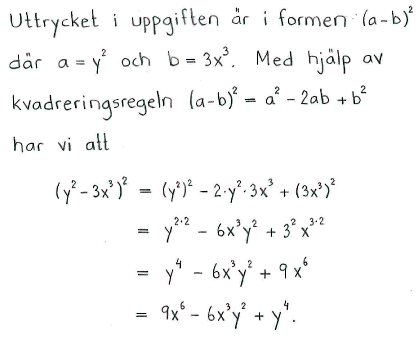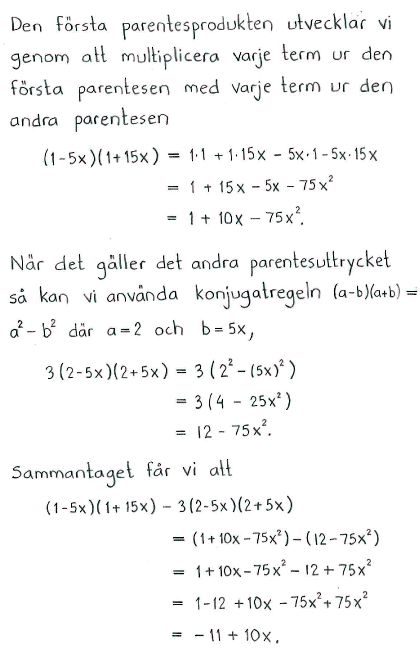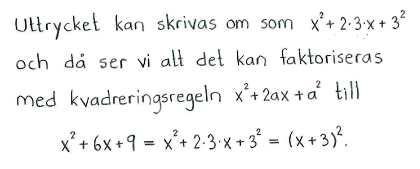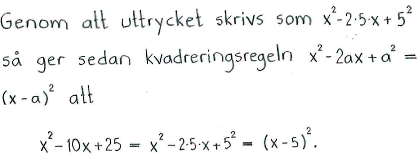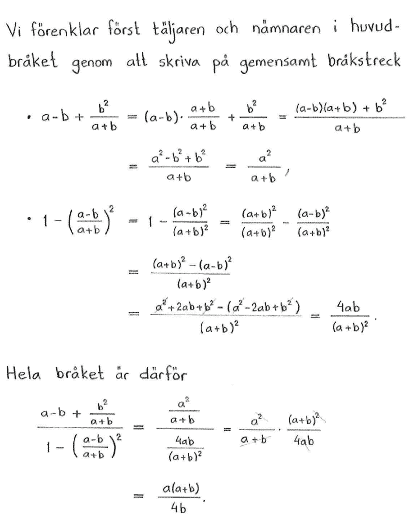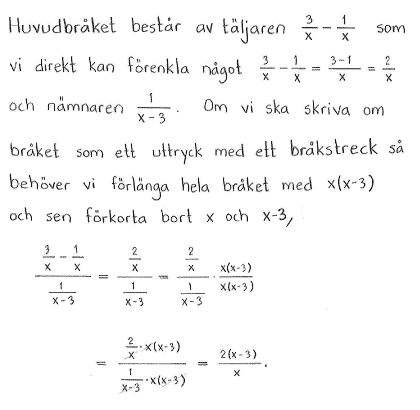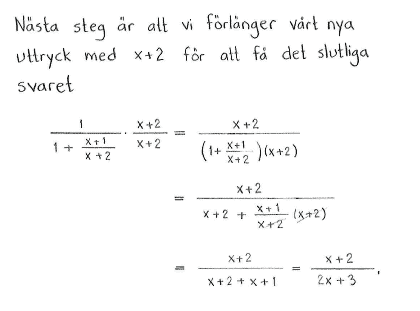2.1 Övningar
Sommarmatte 1
Innehåll[göm] |
[redigera] Övning 2.1:1
Utveckla
| a) | 3x(x-1) | b) | (1+x-x^2)xy | c) | -x^2(4-y^2) |
| d) | x^3y^2\left(\displaystyle \frac{1}{y} - \frac{1}{xy}+1\right) | e) | (x-7)^2 | f) | (5+4y)^2 |
| g) | (y^2-3x^3)^2 | h) | (5x^3+3x^5)^2 | ||
Facit till alla delfrågor
| a) | 3x^2-3x | b) | xy+x^2y-x^3y | c) | -4x^2+x^2y^2 |
| d) | x^3y-x^2y+x^3y^2 | e) | x^2-14x+49 | f) | 16y^2+40y+25 |
| g) | 9x^6-6x^3y^2+y^4 | h) | 9x^{10}+30x^8+25x^6 | ||
Lösning till delfråga a)
|
|
Lösning till delfråga b)
|
|
Lösning till delfråga c)
|
|
Lösning till delfråga d)
|
|
Lösning till delfråga e)
|
|
Lösning till delfråga f)
|
|
Lösning till delfråga g)
|
|
Lösning till delfråga h)
|
|
[redigera] Övning 2.1:2
Utveckla och förenkla så långt som möjligt
| a) | (x-4)(x-5)-3x(2x-3) | b) | (1-5x)(1+15x)-3(2-5x)(2+5x) |
| c) | (3x+4)^2-(3x-2)(3x-8) | d) | (3x^2+2)(3x^2-2)(9x^4+4) |
| e) | (a+b)^2+(a-b)^2 | ||
Facit till alla delfrågor
| a) | -5x^2+20 | b) | 10x-11 |
| c) | 54x | d) | 81x^8-16 |
| e) | 2a^2+2b^2 | ||
Lösning till delfråga a)
|
|
Lösning till delfråga b)
|
|
Lösning till delfråga c)
|
|
Lösning till delfråga d)
|
|
Lösning till delfråga e)
|
|
[redigera] Övning 2.1:3
Faktorisera så långt som möjligt
| a) | x^2-36 | b) | 5x^2-20 | c) | x^2+6x+9 |
| d) | x^2-10x+25 | e) | 18x-2x^3 | f) | 16x^2+8x+1 |
Facit till alla delfrågor
| a) | (x+6)(x-6) | b) | 5(x+2)(x-2) | c) | (x+3)^2 |
| d) | (x-5)^2 | e) | -2x(x+3)(x-3) | f) | (4x+1)^2 |
Lösning till delfråga a)
|
|
Lösning till delfråga b)
|
|
Lösning till delfråga c)
|
|
Lösning till delfråga d)
|
|
Lösning till delfråga e)
|
|
Lösning till delfråga f)
|
|
[redigera] Övning 2.1:4
Bestäm koefficienterna framför \,x\, och \,x^2\, när följande uttryck utvecklas
| a) | (x+2)(3x^2-x+5) |
| b) | (1+x+x^2+x^3)(2-x+x^2+x^4) |
| c) | (x-x^3+x^5)(1+3x+5x^2)(2-7x^2-x^4) |
Facit till alla delfrågor
| a) | 5\, framför \,x^2\,, \,3\, framför \,x |
| b) | 2\, framför \,x^2\,, \,1\, framför \,x |
| \textrm{c) } | 6\, framför \,x^2\,, \,2\, framför \,x |
Lösning till delfråga a)
|
|
Lösning till delfråga b)
|
|
|
|
Lösning till delfråga c)
|
|
[redigera] Övning 2.1:5
Förenkla så långt som möjligt
| a) | \displaystyle \frac{1}{x-x^2}-\displaystyle \frac{1}{x} | b) | \displaystyle \frac{1}{y^2-2y}-\displaystyle \frac{2}{y^2-4} |
| c) | \displaystyle \frac{(3x^2-12)(x^2-1)}{(x+1)(x+2)} | d) | \displaystyle \frac{(y^2+4y+4)(2y-4)}{(y^2+4)(y^2-4)} |
Facit till alla delfrågor
| a) | \displaystyle \frac{1}{1-x} | b) | -\displaystyle \frac{1}{y(y+2)} |
| c) | 3(x-2)(x-1) | d) | \displaystyle \frac{2(y+2)}{y^2+4} |
Lösning till delfråga a)
|
|
Lösning till delfråga b)
|
|
Lösning till delfråga c)
|
|
Lösning till delfråga d)
|
|
|
|
[redigera] Övning 2.1:6
Förenkla så långt som möjligt
| a) | \left(x-y+\displaystyle\frac{x^2}{y-x}\right) \left(\displaystyle\frac{y}{2x-y}-1\right) | b) | \displaystyle \frac{x}{x-2}+\displaystyle \frac{x}{x+3}-2 |
| c) | \displaystyle \frac{2a+b}{a^2-ab}-\frac{2}{a-b} | d) | \displaystyle\frac{a-b+\displaystyle\frac{b^2}{a+b}}{1-\left(\displaystyle\frac{a-b}{a+b}\right)^2} |
Facit till alla delfrågor
| a) | 2y | b) | \displaystyle\frac{-x+12}{(x-2)(x+3)} |
| c) | \displaystyle\frac{b}{a(a-b)} | d) | \displaystyle\frac{a(a+b)}{4b} |
Lösning till delfråga a)
|
|
Lösning till delfråga b)
|
|
Lösning till delfråga c)
|
|
Lösning till delfråga d)
|
|
[redigera] Övning 2.1:7
Förenkla följande bråkuttryck genom att skriva på gemensamt bråkstreck
| a) | \displaystyle \frac{2}{x+3}-\frac{2}{x+5} | b) | x+\displaystyle \frac{1}{x-1}+\displaystyle \frac{1}{x^2} | c) | \displaystyle \frac{ax}{a+1}-\displaystyle \frac{ax^2}{(a+1)^2} |
Facit till alla delfrågorna
| a) | \displaystyle \frac{4}{(x+3)(x+5)} | b) | \displaystyle \frac{x^4-x^3+x^2+x-1}{x^2(x-1)} | c) | \displaystyle \frac{ax(a+1-x)}{(a+1)^2} |
Lösning till delfråga a)
|
|
Lösning till delfråga b)
|
|
Lösning till delfråga c)
|
|
[redigera] Övning 2.1:8
Förenkla följande bråkuttryck genom att skriva på gemensamt bråkstreck
| a) | \displaystyle \frac{\displaystyle\ \frac{x}{x+1}\ }{\ 3+x\ } | b) | \displaystyle \frac{\displaystyle \frac{3}{x}-\displaystyle \frac{1}{x}}{\displaystyle \frac{1}{x-3}} | c) | \displaystyle \frac{1}{1+\displaystyle \frac{1}{1+\displaystyle \frac{1}{1+x}}} |
Facit till alla delfrågor
| a) | \displaystyle \frac{x}{(x+3)(x+1)} | b) | \displaystyle \frac{2(x-3)}{x} | c) | \displaystyle \frac{x+2}{2x+3} |
Lösning till delfråga a)
|
|
Lösning till delfråga b)
|
|
Lösning till delfråga c)
|
|
|
|
