1.1 Olika typer av tal
Sommarmatte 1
| Versionen från 20 april 2007 kl. 13.16 (redigera) Adeline (Diskussion | bidrag) (→Räkneordning i uttryck (Prioriteringsregler)) ← Gå till föregående ändring |
Versionen från 20 april 2007 kl. 13.49 (redigera) (ogör) Adeline (Diskussion | bidrag) (→Räkneoperationer med tal) Gå till nästa ändring → |
||
| Rad 123: | Rad 123: | ||
| ska erhållas. Ett vanligt misstag att skriva 8 + 4/2 + 4, vilket av miniräknaren tolkas | ska erhållas. Ett vanligt misstag att skriva 8 + 4/2 + 4, vilket av miniräknaren tolkas | ||
| som 8 + 2 + 4 = 14. | som 8 + 2 + 4 = 14. | ||
| - | |||
| - | ==Räkneoperationer med tal== | ||
| - | |||
| - | fristående formel dubbla dollar $$ | ||
| - | |||
| - | teori igen | ||
| - | |||
| - | <div class="regel"> | ||
| - | |||
| '''Viktig regel:''' | '''Viktig regel:''' | ||
| Rad 147: | Rad 138: | ||
| </div> | </div> | ||
| + | ==Olika typer av tal== | ||
| + | |||
| + | De tal vi använder oss av för att beskriva antal och mått, mm., | ||
| + | kallas sammanfattningsvis för de reella talen och kan illustreras med hjälp av en tallinje: | ||
| + | |||
| + | |||
| + | De reella talen "fyller" tallinjen, dvs. inga hål eller mellanrum finns någonstans längs | ||
| + | tallinjen. Varje punkt på tallinjen kan anges med hjälp av en följd av decimaler. Mängden av de reella talen är alla decimaltal. Tallinjen visar också talen i storleksordning; ett tal till höger är alltid | ||
| + | större än ett tal till vänster. | ||
| + | Man brukar dela upp de reella talen i följande typer av tal: | ||
| + | |||
| + | |||
| + | ''Naturliga tal'' (symboliseras vanligen med bokstaven N) | ||
| + | |||
| + | De tal som används när man räknar antal: 0, 1, 2, 3, 4, ... | ||
| + | |||
| + | |||
| + | |||
| + | ''Heltal'' ( Z ) | ||
| + | |||
| + | De naturliga talen och deras negativa motsvarigheter: ..., -3, -2, -1, 0, 1, 2, 3, ... | ||
| + | |||
| + | |||
| + | |||
| + | ''Rationella tal'' ( Q ) | ||
| + | |||
| + | Alla tal som kan skrivas som en kvot mellan heltal (bråk), t.ex. | ||
| + | |||
| + | |||
| + | $-\displaystyle \frac{3}{4},\ \frac{3}{2}, \ \frac{37}{128}, \quad\mbox{o.s.v.}$ | ||
| + | |||
| + | |||
| + | |||
| + | Observera att även heltalen räknas som rationella tal, eftersom | ||
| + | |||
| + | |||
| + | $-1 = \displaystyle \frac{-1}{1},\quad 0 = \displaystyle \frac{0}{1},\quad 1 = \displaystyle \frac{1}{1},\quad 2 = \displaystyle \frac{2}{1},\quad\mbox{o.s.v.}$ | ||
| + | |||
| + | |||
| + | |||
| + | Ett rationellt tal kan skrivas på flera olika sätt, eftersom t.ex. | ||
| + | |||
| + | |||
| + | $2 = \displaystyle \frac{2}{1}=\displaystyle \frac{4}{2}=\displaystyle \frac{6}{3}= \displaystyle \frac{8}{4}=\displaystyle \frac{100}{50}=\displaystyle \frac{384}{192}\quad\mbox{o.s.v.}$ | ||
| + | |||
| + | <div class="exempel"> | ||
| + | Exempel 3 | ||
| + | |||
| + | $a) $ | ||
| + | |||
| + | Att multiplicera täljare och nämnare | ||
| + | hos ett rationellt tal med samma tal kallas | ||
| + | förlängning och förändrar | ||
| + | inte talets värde | ||
| + | |||
| + | |||
| + | $\qquad\displaystyle \frac{1}{3} = \frac{1\cdot 2}{3\cdot 2} = \frac{2}{6} = \frac{1\cdot 5}{3\cdot 5} =\frac{5}{15}\quad\mbox{o.s.v.}$ | ||
| + | |||
| + | |||
| + | $b) $ | ||
| + | |||
| + | Att dividera täljare och nämnare hos | ||
| + | ett rationellt tal med samma tal kallas | ||
| + | förkortning och förändrar inte | ||
| + | heller talets värde | ||
| + | |||
| + | |||
| + | $\qquad\displaystyle \frac{75}{105} =\frac{75/5}{105/5} = \frac{15}{21} =\frac{15/3}{21/3} = \frac{5}{7} \quad\mbox{o.s.v.}$ | ||
| + | |||
| + | </div> | ||
| + | |||
| + | |||
| + | |||
| + | ''Irrationella tal'' | ||
| + | |||
| + | De tal på tallinjen som inte kan skrivas som bråk kallas irrationella tal. Exempel | ||
| + | på irrationella tal är de flesta rötter, som | ||
| + | |||
| + | $\sqrt{2} \mbox{ och } \sqrt{3} \mbox{ men även talet } \pi\ \mbox{t.ex.}$ | ||
| + | |||
| + | ===Decimalform=== | ||
| + | |||
| + | Alla typer av reella tal kan skrivas på decimalform, med ett godtyckligt antal decimaler. | ||
| + | Decimalerna som skrivs till höger om decimalkommat anger antal tiondelar, hundradelar, tusendelar, osv., på samma sätt som siffrorna till vänster om decimalkommat anger | ||
| + | antalet ental, tiotal, hundratal, osv. | ||
| + | |||
| + | Komm: Här ska figur 1.1.2 läggas in. | ||
| + | <div class="exempel"> | ||
| + | Exempel 4 | ||
| + | |||
| + | $\displaystyle 1234{,}5678 = 1000 + 200 + 30 + 4 + \frac{5}{10} + \frac{6}{100} + \frac{7}{1000} + \frac{8}{10000}$ | ||
| + | |||
| + | |} | ||
| + | |||
| + | |||
| + | Ett rationellt tal kan skrivas på decimalform genom att utföra divisionen. | ||
| + | Således är talet $ \frac{3}{4} $ samma som "3 dividerat med 4", dvs. 0,75. | ||
| + | |||
| + | [http://sv.wikipedia.org/wiki/Liggande_stolen Beskrivning av liggande stolen] | ||
| + | |||
| + | |||
| + | <div class="exempel"> | ||
| + | Exempel 5 | ||
| + | |||
| + | $a)$ | ||
| + | |||
| + | $\displaystyle\frac{1}{2} = 0{,}5 = 0{,}5\underline{0}$ | ||
| + | |||
| + | |||
| + | $b)$ | ||
| + | |||
| + | $\displaystyle\frac{1}{3} = 0{,}333333... = 0{,}\underline{3}$ | ||
| + | |||
| + | |||
| + | $c)$ | ||
| + | |||
| + | $\displaystyle \frac{5}{12} = 0{,}4166666... = 0{,}41\underline{6}$ | ||
| + | |||
| + | |||
| + | $d)$ | ||
| + | |||
| + | $\displaystyle\frac{1}{7} =0{,}142857142857... = 0{,}\underline{142857}$ | ||
| + | |||
| + | |||
| + | (understrykningen markerar decimaler som upprepas) | ||
| + | |||
| + | |||
| + | </div> | ||
| + | |||
| + | Som synes har de rationella talen ovan en periodisk decimalutveckling, dvs. | ||
| + | decimalutvecklingen slutar alltid med att en viss följd av decimaler upprepas | ||
| + | i all oändlighet. Detta gäller för alla rationella tal och skiljer | ||
| + | dessa från de irrationella, vilka inte har något periodiskt mönster | ||
| + | i sin decimalutveckling. | ||
| + | |||
| + | Omvänt gäller också att alla tal med en periodisk decimalutveckling är rationella tal. | ||
| + | |||
| + | <div class="exempel"> | ||
| + | Exempel 6 | ||
| + | |||
| + | Talen $\pi$ och $\sqrt{2}$ är irrationella tal och har därför inget periodiskt mönster i sin decimalutveckling. | ||
| + | |||
| + | $a)$ | ||
| + | |||
| + | $\pi=3{,}141 \:592 \: 653 \: 589 \:793 \: 238 \: 462 \:643 \ldots $ | ||
| + | |||
| + | |||
| + | $b)$ | ||
| + | |||
| + | $\sqrt{2}=1{,}414 \:213 \: 562 \:373 \: 095 \: 048 \: 801 \:688 \ldots $ | ||
| + | |||
| + | <div class="exempel"> | ||
| + | Exempel 7 | ||
| + | |||
| + | $a)$ | ||
| + | |||
| + | $\displaystyle 0{,}600\ldots = 0{,}6 = \frac{6}{10} = \frac{3}{5} $ | ||
| + | |||
| + | |||
| + | $b)$ | ||
| + | |||
| + | $\displaystyle 0{,}35 = | ||
| + | \frac{35}{100} = \frac{7}{20} $ | ||
| + | |||
| + | $c)$ | ||
| + | |||
| + | $\displaystyle 0{,}0025 = | ||
| + | \frac{25}{10\:000} = \frac{1}{400} $ | ||
| + | </div> | ||
| + | |||
| + | <div class="exempel"> | ||
| + | Exempel 8 | ||
| + | |||
| + | Talet $x=0{,}215151515...$ | ||
| + | är rationellt, eftersom det har en periodisk | ||
| + | decimalutveckling. Vi kan skriva detta rationella | ||
| + | tal som en kvot av två heltal på följande sätt | ||
| + | |||
| + | |||
| + | $\quad 10x = 2{,}151515\ldots$ | ||
| + | |||
| + | |||
| + | $\quad 1000x = 215{,}1515\ldots$ | ||
| + | |||
| + | |||
| + | $\quad 1000x - 10x = 215{,}1515\ldots -2{,}151515\ldots $ | ||
| + | |||
| + | |||
| + | $\quad 990x = 213 $ | ||
| + | |||
| + | |||
| + | $\quad\displaystyle x =\frac{213}{990} = \frac{71}{330}$ | ||
| + | |||
| + | |} | ||
| + | |||
| + | ===Avrundning=== | ||
| + | |||
| + | Eftersom det är opraktiskt att räkna med långa decimalutvecklingar så | ||
| + | avrundar man ofta tal till ett lämpligt antal decimaler. Överenskommelsen som | ||
| + | gäller är att siffrorna 0, 1, 2, 3 och 4 avrundas nedåt | ||
| + | medan 5, 6, 7, 8 och 9 avrundas uppåt. | ||
| + | |||
| + | |||
| + | Vi använder symbolen | ||
| + | |||
| + | $\approx$ | ||
| + | |||
| + | (är ungefär lika med) | ||
| + | för att markera att en avrundning har skett. | ||
| + | <div class="exempel"> | ||
| + | Exempel 9 | ||
| + | |||
| + | Avrundning till 3 decimalers noggrannhet: | ||
| + | |||
| + | $a)$ | ||
| + | |||
| + | $1{,}0004 \approx 1,000$ | ||
| + | |||
| + | |||
| + | $b)$ | ||
| + | |||
| + | $ 0{,}9999 \approx 1{,}000$ | ||
| + | |||
| + | |||
| + | $c)$ | ||
| + | |||
| + | $2{,}9994999 \approx 2{,}999$ | ||
| + | |||
| + | |||
| + | $d)$ | ||
| + | |||
| + | $ 2{,}99950 \approx 3{,}000$ | ||
| + | </div> | ||
| + | |||
| + | <div class="exempel"> | ||
| + | Exempel 10 | ||
| + | |||
| + | Avrundning till 4 decimalers noggrannhet: | ||
| + | |||
| + | |||
| + | $a)$ | ||
| + | |||
| + | $\pi \approx 3{,}1416 $ | ||
| + | |||
| + | |||
| + | $b)$ | ||
| + | |||
| + | $\displaystyle\frac{2}{3} \approx 0{,}6667 $ | ||
| + | |||
| + | |||
| + | $c)$ | ||
| + | |||
| + | $\displaystyle \frac{8}{7} \approx 1{,}1429 $ | ||
| + | |||
| + | |} | ||
| + | |||
| + | ==Jämförelse av tal== | ||
| + | |||
| + | Man anger storleksförhållandet mellan tal med hjälp av symbolerna | ||
| + | > (är större än), < (är mindre än) och = (är lika med). | ||
| + | Storleksförhållandet mellan två tal kan avgöras dels genom | ||
| + | att skriva talen i decimalform, eller genom att skriva rationella tal som bråk | ||
| + | med gemensam nämnare. | ||
| + | |||
| + | <div class="exempel"> | ||
| + | Exempel 11 | ||
| + | |||
| + | $a)$ Vilket är störst av talen | ||
| + | $\ \displaystyle \frac{1}{3}\ $ och $\ 0,33$ ? | ||
| + | |||
| + | |||
| + | <b>Lösning</b> | ||
| + | |||
| + | Vi har att | ||
| + | |||
| + | |||
| + | $\qquad\displaystyle x =\frac{1}{3} = \frac{100}{300}\quad$ och $\quad\displaystyle y = 0,33 =\frac{33}{100} = \frac{99}{300}$. | ||
| + | |||
| + | Alltså är $ x>y $ eftersom | ||
| + | $100/300 > 99/300$. | ||
| + | |||
| + | Alternativt så kan man se att | ||
| + | $1/3>0{,}33 $ eftersom | ||
| + | $ 1/3=0{,}3333\ldots > | ||
| + | 0{,}33$. | ||
| + | |||
| + | |||
| + | $b)$ Vilket tal är störst av | ||
| + | $\ \displaystyle \frac{2}{5}\ | ||
| + | $ | ||
| + | och $\ \displaystyle \frac{3}{7} | ||
| + | $ ? | ||
| + | |||
| + | |||
| + | <b>Lösning:</b> | ||
| + | |||
| + | Skriv talen med gemensam nämnare, t.ex. | ||
| + | 35: | ||
| + | |||
| + | $\quad\displaystyle \frac{2}{5} = | ||
| + | \frac{14}{35}\ \ $ och $\ \ | ||
| + | \displaystyle\frac{3}{7} = \frac{15}{35} | ||
| + | $. | ||
| + | |||
| + | Alltså är $\ \displaystyle | ||
| + | \frac{3}{7}>\frac{2}{5}\ $ eftersom | ||
| + | $\ \displaystyle \frac{15}{35} > | ||
| + | \frac{14}{35}$. | ||
| + | </div> | ||
| + | |||
| + | <div class="exempel"> | ||
| + | Råd för inläsning | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | '''Att tänka på''' | ||
| + | |||
| + | Vara noggrann! Många lösningar blir fel på grund av misstag i avskriften eller andra enkla fel, och inte för att du skulle ha tänkt fel. | ||
| + | |||
| + | |||
| + | '''Lästips''' | ||
| + | |||
| + | För dig som vill fördjupa dig ytterligare eller behöver en längre förklaring så vill vi tipsa om | ||
| + | |||
| + | [http://www.theducation.se/kurser/gymaa/kursmoment/aaritmetik_sam/aaritmetik_sam.htm Theducations sammanfattning av Aritmetiken med övningar att träna själv på] | ||
| + | |||
| + | [http://en.wikipedia.org/wiki/Arithmetic Läs mer om Aritmetik i engelska Wikipedia] | ||
| + | |||
| + | [http://www-groups.dcs.st-and.ac.uk/~history/HistTopics/Zero.html Vem upptäckte Nollan? Läs mer i "The MacTutor History of Mathematics archive"] | ||
| + | |||
| + | [http://www.fritext.se/matte/grunder/posi3.html Liggande stolen - en beskrivning] | ||
| + | |||
| + | [http://en.wikipedia.org/wiki/0.999... Visste du att 0,999... = 1?] | ||
| + | |||
| + | '''Länktips''' | ||
| + | |||
| + | Hur många färger behövs det för att färglägga en karta? Hur många gånger måste man blanda en kortlek? Vilket är det största primtalet? Finns det några "turnummer"? Vilket är det vackraste talet? Lyssna till den kända författaren och matematikern Simon Singh, som bland annat berättar om de magiska talen 4 och 7, om primtalen, Keplers högar och om nollan. | ||
| + | |||
| + | [http://www.bbc.co.uk/radio4/science/5numbers1.shtml Lyssna på BBC-programmen "5 Numbers"] | ||
| + | |||
| + | [http://www.bbc.co.uk/radio4/science/another5.shtml Lyssna på BBC-programmen "Another 5 numbers"] | ||
| + | |||
| + | |} | ||
| + | |||
| + | |||
| + | © Copyright 2006, KTH Matematik | ||
| ==Räkneoperationer med tal== | ==Räkneoperationer med tal== | ||
Versionen från 20 april 2007 kl. 13.49
1.1 Olika typer av talInnehåll:
Läromål: Efter detta avsnitt ska du ha lärt dig att:
|
||
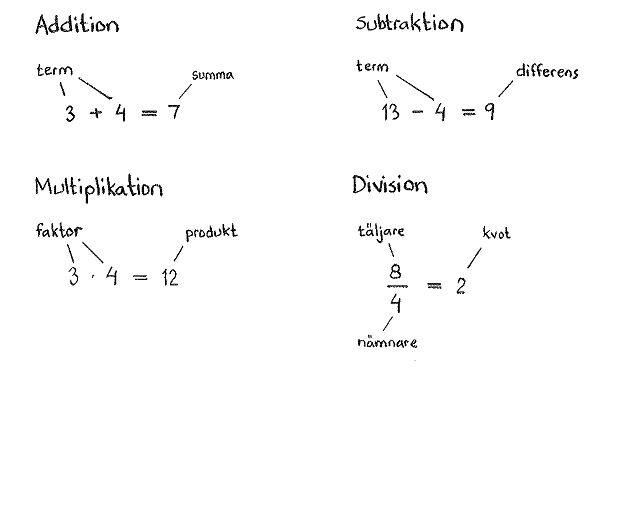
TeoriRäkneoperationer med talAtt arbeta med tal innebär att man utför en rad räkneoperationer de grundläggande är de fyra räknesätten. Här följer några begrepp som är bra att kunna för att förstå matematisk text:
Räkneordning i uttryck (Prioriteringsregler)När flera räknesätt förekommer i ett matematiskt uttryck är det viktigt att man har en överenskommelse om i vilken ordning operationerna ska utföras. Följande gäller:
Exempel 1 Hakparanteserna visar vilken operation som utförs i varje led.
"Osynliga" parenteserVid division ska täljare och nämnare beräknas var för sig innan divisionen utförs. Man kan därför säga att det finns "osynliga parenteser" omkring täljare och nämnare.
Exempel 1 Hakparanteserna visar vilken operation som utförs i varje led.
Speciellt viktigt är detta vid användandet av miniräknare. Divisionen
Viktig regel: $$dubbeldollar$$ </div> Exempel 1 Exempeltext, använd nedanstående numrering
Olika typer av talDe tal vi använder oss av för att beskriva antal och mått, mm., kallas sammanfattningsvis för de reella talen och kan illustreras med hjälp av en tallinje:
De tal som används när man räknar antal: 0, 1, 2, 3, 4, ...
Heltal ( Z ) De naturliga talen och deras negativa motsvarigheter: ..., -3, -2, -1, 0, 1, 2, 3, ...
Rationella tal ( Q ) Alla tal som kan skrivas som en kvot mellan heltal (bråk), t.ex.
Observera att även heltalen räknas som rationella tal, eftersom
Ett rationellt tal kan skrivas på flera olika sätt, eftersom t.ex.
Exempel 3 $a) $ Att multiplicera täljare och nämnare hos ett rationellt tal med samma tal kallas förlängning och förändrar inte talets värde
Att dividera täljare och nämnare hos ett rationellt tal med samma tal kallas förkortning och förändrar inte heller talets värde
Irrationella tal De tal på tallinjen som inte kan skrivas som bråk kallas irrationella tal. Exempel på irrationella tal är de flesta rötter, som $\sqrt{2} \mbox{ och } \sqrt{3} \mbox{ men även talet } \pi\ \mbox{t.ex.}$ DecimalformAlla typer av reella tal kan skrivas på decimalform, med ett godtyckligt antal decimaler. Decimalerna som skrivs till höger om decimalkommat anger antal tiondelar, hundradelar, tusendelar, osv., på samma sätt som siffrorna till vänster om decimalkommat anger antalet ental, tiotal, hundratal, osv. Komm: Här ska figur 1.1.2 läggas in. Exempel 4 $\displaystyle 1234{,}5678 = 1000 + 200 + 30 + 4 + \frac{5}{10} + \frac{6}{100} + \frac{7}{1000} + \frac{8}{10000}$ |}
Beskrivning av liggande stolen
Exempel 5 $a)$ $\displaystyle\frac{1}{2} = 0{,}5 = 0{,}5\underline{0}$
$\displaystyle\frac{1}{3} = 0{,}333333... = 0{,}\underline{3}$
$\displaystyle \frac{5}{12} = 0{,}4166666... = 0{,}41\underline{6}$
$\displaystyle\frac{1}{7} =0{,}142857142857... = 0{,}\underline{142857}$
Som synes har de rationella talen ovan en periodisk decimalutveckling, dvs. decimalutvecklingen slutar alltid med att en viss följd av decimaler upprepas i all oändlighet. Detta gäller för alla rationella tal och skiljer dessa från de irrationella, vilka inte har något periodiskt mönster i sin decimalutveckling. Omvänt gäller också att alla tal med en periodisk decimalutveckling är rationella tal. Exempel 6 Talen $\pi$ och $\sqrt{2}$ är irrationella tal och har därför inget periodiskt mönster i sin decimalutveckling. $a)$ $\pi=3{,}141 \:592 \: 653 \: 589 \:793 \: 238 \: 462 \:643 \ldots $
$\sqrt{2}=1{,}414 \:213 \: 562 \:373 \: 095 \: 048 \: 801 \:688 \ldots $ Exempel 7 $a)$ $\displaystyle 0{,}600\ldots = 0{,}6 = \frac{6}{10} = \frac{3}{5} $
$\displaystyle 0{,}35 = \frac{35}{100} = \frac{7}{20} $ $c)$ $\displaystyle 0{,}0025 = \frac{25}{10\:000} = \frac{1}{400} $ Exempel 8 Talet $x=0{,}215151515...$ är rationellt, eftersom det har en periodisk decimalutveckling. Vi kan skriva detta rationella tal som en kvot av två heltal på följande sätt
|} AvrundningEftersom det är opraktiskt att räkna med långa decimalutvecklingar så avrundar man ofta tal till ett lämpligt antal decimaler. Överenskommelsen som gäller är att siffrorna 0, 1, 2, 3 och 4 avrundas nedåt medan 5, 6, 7, 8 och 9 avrundas uppåt.
$\approx$ (är ungefär lika med) för att markera att en avrundning har skett. Exempel 9 Avrundning till 3 decimalers noggrannhet: $a)$ $1{,}0004 \approx 1,000$
$ 0{,}9999 \approx 1{,}000$
$2{,}9994999 \approx 2{,}999$
$ 2{,}99950 \approx 3{,}000$ Exempel 10 Avrundning till 4 decimalers noggrannhet:
$\pi \approx 3{,}1416 $
$\displaystyle\frac{2}{3} \approx 0{,}6667 $
$\displaystyle \frac{8}{7} \approx 1{,}1429 $ |} Jämförelse av talMan anger storleksförhållandet mellan tal med hjälp av symbolerna > (är större än), < (är mindre än) och = (är lika med). Storleksförhållandet mellan två tal kan avgöras dels genom att skriva talen i decimalform, eller genom att skriva rationella tal som bråk med gemensam nämnare. Exempel 11 $a)$ Vilket är störst av talen $\ \displaystyle \frac{1}{3}\ $ och $\ 0,33$ ?
Vi har att
Alltså är $ x>y $ eftersom $100/300 > 99/300$. Alternativt så kan man se att $1/3>0{,}33 $ eftersom $ 1/3=0{,}3333\ldots > 0{,}33$.
Skriv talen med gemensam nämnare, t.ex. 35: $\quad\displaystyle \frac{2}{5} = \frac{14}{35}\ \ $ och $\ \ \displaystyle\frac{3}{7} = \frac{15}{35} $. Alltså är $\ \displaystyle \frac{3}{7}>\frac{2}{5}\ $ eftersom $\ \displaystyle \frac{15}{35} > \frac{14}{35}$. Råd för inläsning |- | Att tänka på Vara noggrann! Många lösningar blir fel på grund av misstag i avskriften eller andra enkla fel, och inte för att du skulle ha tänkt fel.
För dig som vill fördjupa dig ytterligare eller behöver en längre förklaring så vill vi tipsa om Theducations sammanfattning av Aritmetiken med övningar att träna själv på Läs mer om Aritmetik i engelska Wikipedia Vem upptäckte Nollan? Läs mer i "The MacTutor History of Mathematics archive" Liggande stolen - en beskrivning Länktips Hur många färger behövs det för att färglägga en karta? Hur många gånger måste man blanda en kortlek? Vilket är det största primtalet? Finns det några "turnummer"? Vilket är det vackraste talet? Lyssna till den kända författaren och matematikern Simon Singh, som bland annat berättar om de magiska talen 4 och 7, om primtalen, Keplers högar och om nollan. Lyssna på BBC-programmen "5 Numbers" Lyssna på BBC-programmen "Another 5 numbers" |}
Räkneoperationer med talteori igen Råd för inläsning Tänk på att: text Lästips stående Länktips stående
|