2.1 Inledning till integraler
Sommarmatte 2
| Versionen från 15 juni 2007 kl. 14.50 (redigera) KTH.SE:u1tyze7e (Diskussion | bidrag) (Korrekturläst (delvis)) ← Gå till föregående ändring |
Nuvarande version (9 juli 2007 kl. 15.31) (redigera) (ogör) KTH.SE:u1rp004j (Diskussion | bidrag) (→Area under en funktionskurva) |
||
| (En mellanliggande version visas inte.) | |||
| Rad 36: | Rad 36: | ||
| Vi har tidigare sett att lutningen på en funktionskurva är intressant. Den ger oss information om hur funktionen ändras och har stor betydelse i många tillämpningar. | Vi har tidigare sett att lutningen på en funktionskurva är intressant. Den ger oss information om hur funktionen ändras och har stor betydelse i många tillämpningar. | ||
| På ett liknande sätt är den area som bildas mellan en funktionskurva och ''x''-axeln betydelsefull. Den är naturligtvis beroende av funktionskurvans utseende och därmed intimt besläktad med funktionen i fråga. Det är lätt att inse att denna area har en praktisk betydelse i många olika sammanhang. <br> | På ett liknande sätt är den area som bildas mellan en funktionskurva och ''x''-axeln betydelsefull. Den är naturligtvis beroende av funktionskurvans utseende och därmed intimt besläktad med funktionen i fråga. Det är lätt att inse att denna area har en praktisk betydelse i många olika sammanhang. <br> | ||
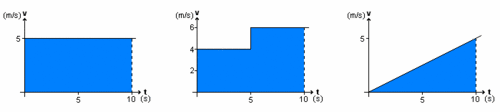
| - | Om ett föremål rör sig så kan vi beskriva dess hastighet ''v'' efter tiden ''t'' i ett ''v-t''-diagram. Vi ser här tre olika exempel: | + | Om ett föremål rör sig så kan vi beskriva dess hastighet ''v'' efter tiden ''t'' i ett ''v-t''-diagram. Vi ser här tre olika fiktiva exempel: |
| - | $$v(t)=5,\qquad v(t)= \left \{ \matrix{4, \quad 0 \le t < 5\\ 6, \quad 5 \le t \le 10}\right.\quad\text{och}\quad v(t) =0{,}5\,\mbox{.}$$ | + | $$v(t)=5,\qquad v(t)= \left \{ \matrix{4, \quad 0 \le t < 5\\ 6, \quad 5 \le t \le 10}\right.\quad\text{och}\quad v(t) =0{,}5 t\,\mbox{.}$$ |
| [[Bild:Vt-diagram.gif|500px|center|]] | [[Bild:Vt-diagram.gif|500px|center|]] | ||
| Rad 70: | Rad 70: | ||
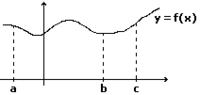
| Med integralen av den positiva funktionen $\,f(x)\,$ från $\,a\,$ till $\,b\,$ menas arean mellan kurvan $\,y=f(x)\,$ och ''x''-axeln från $\,x=a\,$ till $\,x=b\,$ , vilket med symboler skrivs | Med integralen av den positiva funktionen $\,f(x)\,$ från $\,a\,$ till $\,b\,$ menas arean mellan kurvan $\,y=f(x)\,$ och ''x''-axeln från $\,x=a\,$ till $\,x=b\,$ , vilket med symboler skrivs | ||
| - | $$\int_{a}^{b} f(x)\, dx\,\mbox{.}$$ | + | $$\int_{a}^{\,b} f(x)\, dx\,\mbox{.}$$ |
| Talen $\,a\,$ och $\,b\,$ kallas undre respektive övre integrationsgräns, $\,f(x)\,$ kallas integrand och $\,x\,$ integrationsvariabel. | Talen $\,a\,$ och $\,b\,$ kallas undre respektive övre integrationsgräns, $\,f(x)\,$ kallas integrand och $\,x\,$ integrationsvariabel. | ||
| Rad 79: | Rad 79: | ||
| [[Bild:Integral3.gif|200px|right|]] | [[Bild:Integral3.gif|200px|right|]] | ||
| Ur definitionen följer direkt att | Ur definitionen följer direkt att | ||
| - | $$\int_{a}^{b} f(x)\, dx + \int_{b}^{c} f(x)\, dx = \int_{a}^{c} f(x)\, dx\,\mbox{.}$$ | + | $$\int_{a}^{\,b} f(x)\, dx + \int_{b}^{\,c} f(x)\, dx = \int_{a}^{\,c} f(x)\, dx\,\mbox{.}$$ |
| Rad 123: | Rad 123: | ||
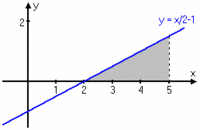
| <li>$\displaystyle \int_{2}^{5} \Bigl(\displaystyle \frac{x}{2} -1 \Bigr) \, dx$ <br><br> | <li>$\displaystyle \int_{2}^{5} \Bigl(\displaystyle \frac{x}{2} -1 \Bigr) \, dx$ <br><br> | ||
| Integralen kan tolkas som arean under linjen $\,y=x/2-1\,$ från $\,x = 2\,$ till $\,x = 5\,$, | Integralen kan tolkas som arean under linjen $\,y=x/2-1\,$ från $\,x = 2\,$ till $\,x = 5\,$, | ||
| - | dvs. en triangel med basen 3 och höjden 1,5. <br> | + | dvs. en triangel med basen 3 och höjden 1,5 <br> |
| - | $\quad\displaystyle\int_{2}^{5} \Bigl(\frac{x}{2} -1 \Bigr) \, dx = \frac{3 \cdot 1{,}5}{2} = 2{,}25$<br><br> | + | $\qquad\displaystyle\int_{2}^{5} \Bigl(\frac{x}{2} -1 \Bigr) \, dx = \frac{3 \cdot 1{,}5}{2} = 2{,}25\,\mbox{.}$<br><br> |
| </ol> | </ol> | ||
| [[Bild:Integral7.gif|200px|right]] | [[Bild:Integral7.gif|200px|right]] | ||
| <ol type="a" start=3> | <ol type="a" start=3> | ||
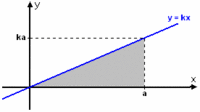
| - | <li>$\displaystyle \int_{0}^{a} kx \, dx\,\mbox{,}\qquad$ där $k>0\,$.<br><br> | + | <li>$\displaystyle \int_{0}^{a} kx \, dx\,\mbox{}\quad$ där $k>0\,$.<br><br> |
| Integralen kan tolkas som arean under linjen $\,y=kx\,$ från $\,x = 0\,$ till $\,x = a\,$, dvs. en triangel | Integralen kan tolkas som arean under linjen $\,y=kx\,$ från $\,x = 0\,$ till $\,x = a\,$, dvs. en triangel | ||
| - | med basen $\,a\,$ och höjden $\,ka\,$.<br> | + | med basen $\,a\,$ och höjden $\,ka\,$<br> |
| - | $\quad\displaystyle \int_{0}^{a} kx\,dx = \frac{a \cdot ka}{2} = \frac{ka^2}{2}\,\mbox{.}$ | + | $\qquad\displaystyle \int_{0}^{\,a} kx\,dx = \frac{a \cdot ka}{2} = \frac{ka^2}{2}\,\mbox{.}$ |
| </ol> | </ol> | ||
| Rad 163: | Rad 163: | ||
| [[Bild:Integral8.gif|300px|center|]] | [[Bild:Integral8.gif|300px|center|]] | ||
| - | $$A(x) = \int_{a}^x f(t) \, dt\,\mbox{.}$$ | + | $$A(x) = \int_{a}^{\,x} f(t) \, dt\,\mbox{.}$$ |
| Rad 172: | Rad 172: | ||
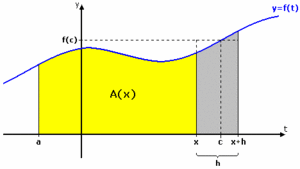
| - | Den skuggade arean kan för varje $\,x\,$ beskrivas på två sätt, dels som $\,A(x+h) - A(x)\,$, men även som $\,h \cdot f(c)\,$, för något $\,c\,$ mellan $\,x\,$ och $\,x + h\,$, det vill säga: | + | Den gråskuggade arean kan för varje $\,x\,$ beskrivas på två sätt, dels som $\,A(x+h) - A(x)\,$, men även som $\,h \cdot f(c)\,$, för något $\,c\,$ mellan $\,x\,$ och $\,x + h\,$, det vill säga: |
| $$\eqalign{A(x+h) - A(x) &= h \cdot f(c)\,\mbox{,}\qquad \textrm {eller}\cr \frac{A(x+h) - A(x)}{h} &= f(c)}$$ | $$\eqalign{A(x+h) - A(x) &= h \cdot f(c)\,\mbox{,}\qquad \textrm {eller}\cr \frac{A(x+h) - A(x)}{h} &= f(c)}$$ | ||
| Rad 181: | Rad 181: | ||
| ==Beräkning av integraler== | ==Beräkning av integraler== | ||
| För att kunna använda primitiva funktioner vid beräkning av en bestämd integral, noterar vi först att om $\,F\,$ är en primitiv funktion till $\,f\,$ så är | För att kunna använda primitiva funktioner vid beräkning av en bestämd integral, noterar vi först att om $\,F\,$ är en primitiv funktion till $\,f\,$ så är | ||
| - | $$\int_{a}^{b} f(t) \, dt = F(b) + C$$ | + | $$\int_{a}^{\,b} f(t) \, dt = F(b) + C$$ |
| där konstanten $\,C\,$ måste väljas så att högerledet blir noll när $\,b=a\,$, dvs. | där konstanten $\,C\,$ måste väljas så att högerledet blir noll när $\,b=a\,$, dvs. | ||
| - | $$\int_{a}^{a} f(t) \, dt = F(a) + C = 0$$ | + | $$\int_{a}^{\,a} f(t) \, dt = F(a) + C = 0$$ |
| vilket ger att $\,C=-F(a)\,$. Om vi sammanfattar har vi alltså att | vilket ger att $\,C=-F(a)\,$. Om vi sammanfattar har vi alltså att | ||
| - | $$\int_{a}^{b} f(t) \, dt = F(b) - F(a)\,\mbox{.}$$ | + | $$\int_{a}^{\,b} f(t) \, dt = F(b) - F(a)\,\mbox{.}$$ |
| - | Vi kan naturligtvis här lika gärna välja $x$ som integrationsvariabel och skriva | + | Vi kan naturligtvis här lika gärna välja $\,x\,$ som integrationsvariabel och skriva |
| - | $$\int_{a}^{b} f(x) \, dx = F(b) - F(a)\,\mbox{.}$$ | + | $$\int_{a}^{\,b} f(x) \, dx = F(b) - F(a)\,\mbox{.}$$ |
| Vid beräkning av integraler utför man detta i två steg. Först bestämmer man en primitiv funktion och sedan sätter man in integrationsgränserna. Man skriver vanligtvis | Vid beräkning av integraler utför man detta i två steg. Först bestämmer man en primitiv funktion och sedan sätter man in integrationsgränserna. Man skriver vanligtvis | ||
| - | $$\int_{a}^{b} f(x) \, dx = \Bigl[\,F(x)\,\Bigr]_{a}^{b} = F(b) - F(a)\,\mbox{.}$$ | + | $$\int_{a}^{\,b} f(x) \, dx = \Bigl[\,F(x)\,\Bigr]_{a}^{b} = F(b) - F(a)\,\mbox{.}$$ |
| Rad 222: | Rad 222: | ||
| <li>$\displaystyle\int (x^4 - 2x^3 + 4x - 7)\,dx = \displaystyle\frac{x^5}{5} - \displaystyle\frac{2x^4}{4} + \displaystyle\frac{4x^2}{2} - 7x + C = \displaystyle\frac{x^5}{5} - \displaystyle\frac{x^4}{2} + 2x^2 - 7x + C$ <br><br> | <li>$\displaystyle\int (x^4 - 2x^3 + 4x - 7)\,dx = \displaystyle\frac{x^5}{5} - \displaystyle\frac{2x^4}{4} + \displaystyle\frac{4x^2}{2} - 7x + C = \displaystyle\frac{x^5}{5} - \displaystyle\frac{x^4}{2} + 2x^2 - 7x + C$ <br><br> | ||
| <li>$\displaystyle\int \Bigl(\displaystyle\frac{3}{x^2} -\frac{1}{2x^3} \Bigr) dx = \int \Bigl( 3x^{-2} - \frac{1}{2} x^{-3} \Bigr) dx = \frac{3x^{-1}}{-1} - \frac{1}{2} \cdot \frac{x^{-2}}{(-2)} + C$ <br> | <li>$\displaystyle\int \Bigl(\displaystyle\frac{3}{x^2} -\frac{1}{2x^3} \Bigr) dx = \int \Bigl( 3x^{-2} - \frac{1}{2} x^{-3} \Bigr) dx = \frac{3x^{-1}}{-1} - \frac{1}{2} \cdot \frac{x^{-2}}{(-2)} + C$ <br> | ||
| - | $\displaystyle\phantom{\int \Bigl(\displaystyle\frac{3}{x^2} -\frac{1}{2x^3} \Bigr) dx}{}= - 3x^{-1} + {\textstyle\frac{1}{4}}x^{-2} + C = -\frac{3}{x} + \frac{1}{4x^2} + C$ <br><br> | + | $\displaystyle\phantom{\int \Bigl(\displaystyle\frac{3}{x^2} -\frac{1}{2x^3} \Bigr) dx}{}= - 3x^{-1} + {\textstyle\frac{1}{4}}x^{-2} + C = -\frac{3}{x} + \frac{1}{4x^2} + C\vphantom{\Biggl(}$ <br><br> |
| <li>$\displaystyle\int \displaystyle\frac{2}{3x} \,dx = \int \frac{2}{3} \cdot \frac{1}{x} \, dx = {\textstyle\frac{2}{3}} \ln |x| + C$ <br><br> | <li>$\displaystyle\int \displaystyle\frac{2}{3x} \,dx = \int \frac{2}{3} \cdot \frac{1}{x} \, dx = {\textstyle\frac{2}{3}} \ln |x| + C$ <br><br> | ||
| <li>$\displaystyle\int ( e^x - \cos x - \sin x ) \, dx = e^x - \sin x + \cos x +C$ | <li>$\displaystyle\int ( e^x - \cos x - \sin x ) \, dx = e^x - \sin x + \cos x +C$ | ||
| Rad 229: | Rad 229: | ||
| </div> | </div> | ||
| - | ==Kompensation för ”inre derivatan”== | + | ==Kompensation för ”inre derivata”== |
| Vid derivering av en sammansatt funktion använder man sig av ''kedjeregeln'', som innebär att man '''multiplicerar''' med den ''inre derivatan''. Om den inre funktionen då är linjär så blir den inre derivatan en konstant. Vid integrering av en sådan funktion måste man därför '''dividera''' med den inre derivatan för att kompensera för detta. | Vid derivering av en sammansatt funktion använder man sig av ''kedjeregeln'', som innebär att man '''multiplicerar''' med den ''inre derivatan''. Om den inre funktionen då är linjär så blir den inre derivatan en konstant. Vid integrering av en sådan funktion måste man därför '''dividera''' med den inre derivatan för att kompensera för detta. | ||
| Rad 259: | Rad 259: | ||
| Med hjälp av beräkningsformeln för integraler är det lätt att visa följande räkneregler för integraler: | Med hjälp av beräkningsformeln för integraler är det lätt att visa följande räkneregler för integraler: | ||
| - | # $\displaystyle \int_{b}^{a} f(x) \, dx = - \displaystyle \int_{a}^{b} f(x) \, dx\,\mbox{,}$ | + | # $\displaystyle \int_{b}^{\,a} f(x) \, dx = - \displaystyle \int_{a}^{\,b} f(x) \, dx\,\mbox{,}$ |
| - | # $\displaystyle \int_{a}^{b} f(x) \, dx + \displaystyle \int_{a}^{b} g(x) \, dx = \displaystyle \int_{a}^{b} (f(x) + g(x)) \, dx\,\mbox{,}\vphantom{\Biggl(}$ | + | # $\displaystyle \int_{a}^{\,b} f(x) \, dx + \displaystyle \int_{a}^{\,b} g(x) \, dx = \displaystyle \int_{a}^{\,b} (f(x) + g(x)) \, dx\,\mbox{,}\vphantom{\Biggl(}$ |
| - | # $\displaystyle \int_{a}^{b} k \cdot f(x)\, dx = k \displaystyle \int_{a}^{b} f(x)\, dx\,\mbox{,}\vphantom{\Biggl(}$ | + | # $\displaystyle \int_{a}^{\,b} k \cdot f(x)\, dx = k \displaystyle \int_{a}^{\,b} f(x)\, dx\,\mbox{,}\vphantom{\Biggl(}$ |
| - | # $\displaystyle \int_{a}^{b} f(x) \, dx + \displaystyle \int_{b}^{c} f(x)\, dx = \displaystyle \int_{a}^{c} f(x)\, dx\,\mbox{.}$ | + | # $\displaystyle \int_{a}^{\,b} f(x) \, dx + \displaystyle \int_{b}^{\,c} f(x)\, dx = \displaystyle \int_{a}^{\,c} f(x)\, dx\,\mbox{.}$ |
| Rad 271: | Rad 271: | ||
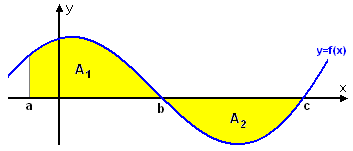
| - | $$A_1 = \displaystyle \int_{a}^{b} f(x)\, dx \quad , \quad A_2 = -\displaystyle \int_{b}^{c} f(x)\, dx$$ | + | $$A_1 = \displaystyle \int_{a}^{\,b} f(x)\, dx \quad , \quad A_2 = -\displaystyle \int_{b}^{\,c} f(x)\, dx$$ |
| - | Den sammanlagda arean blir $\qquad A_1 + A_2 = \displaystyle \int_{a}^{b} f(x)\, dx - \displaystyle \int_{b}^{c} f(x)\, dx\,$. | + | Den sammanlagda arean blir $\qquad A_1 + A_2 = \displaystyle \int_{a}^{\,b} f(x)\, dx - \displaystyle \int_{b}^{\,c} f(x)\, dx\,$. |
| ''Anm:''<br> | ''Anm:''<br> | ||
| Rad 283: | Rad 283: | ||
| [[Bild:Integral12.gif|200px|right|]] | [[Bild:Integral12.gif|200px|right|]] | ||
| <ol type="a"> | <ol type="a"> | ||
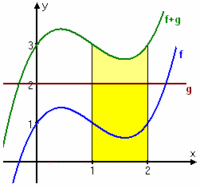
| - | <li>$\displaystyle \int_{1}^{2} (x^3 - 3x^2 + 2x + 1) \, dx + \int_{1}^{2} 2 \, dx$<br> | + | <li>$\displaystyle \int_{1}^{2} (x^3 - 3x^2 + 2x + 1) \, dx + \int_{1}^{2} 2 \, dx\vphantom{\Biggl(}$<br> |
| $\displaystyle\qquad{}=\int_{1}^{2} (x^3 - 3x^2 + 2x + 1+2) \, dx$<br> | $\displaystyle\qquad{}=\int_{1}^{2} (x^3 - 3x^2 + 2x + 1+2) \, dx$<br> | ||
| - | $\displaystyle\qquad{}= \Bigl[\,\frac{1}{4}x^4 - x^3 + x^2 + 3x\,\Bigr]_{1}^{2}$<br> | + | $\displaystyle\qquad{}= \Bigl[\,{\textstyle\frac{1}{4}}x^4 - x^3 + x^2 + 3x\,\Bigr]_{1}^{2}\vphantom{\Biggl(}$<br> |
| - | $\displaystyle\qquad{}= \bigl({\textstyle\frac{1}{4}}\cdot 4-2^3 + 2^2+3\cdot 2\bigr) - \bigl({\textstyle\frac{1}{4}}\cdot 1^4 - 1^3 + 1^2 +3\cdot 1\bigr)$ <br> | + | $\displaystyle\qquad{}= \bigl({\textstyle\frac{1}{4}}\cdot 4-2^3 + 2^2+3\cdot 2\bigr)$<br> |
| - | $\displaystyle\qquad{}=6-3-{\textstyle\frac{1}{4}} =\frac{11}{4}$ <br><br> | + | $\qquad\qquad{} - \bigl({\textstyle\frac{1}{4}}\cdot 1^4 - 1^3 + 1^2 +3\cdot 1\bigr)\vphantom{\Biggl(}$ <br> |
| + | $\displaystyle\qquad{}=6-3-{\textstyle\frac{1}{4}} ={\textstyle\frac{11}{4}}$ <br><br> | ||
| </ol> | </ol> | ||
| [[Bild:Integral13.gif|200px|right|]] | [[Bild:Integral13.gif|200px|right|]] | ||
| <ol type="a" start=2> | <ol type="a" start=2> | ||
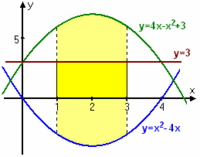
| - | <li>$\displaystyle \int_{1}^{3} (x^2 - 4x) \, dx + \displaystyle \int_{1}^{3} (4x - x^2 + 3) \, dx$<br> | + | <li>$\displaystyle \int_{1}^{3} (x^2 - 4x) \, dx + \displaystyle \int_{1}^{3} (4x - x^2 + 3) \, dx\vphantom{\Biggl(}$<br> |
| $\displaystyle\qquad{}=\int_{1}^{3} 3 \, dx = \Bigl[\,3x\,\Bigr]_{1}^{3} = 3\cdot 3 - 3\cdot 1 = 6$ <br><br> | $\displaystyle\qquad{}=\int_{1}^{3} 3 \, dx = \Bigl[\,3x\,\Bigr]_{1}^{3} = 3\cdot 3 - 3\cdot 1 = 6$ <br><br> | ||
| </ol> | </ol> | ||
| + | |||
| + | |||
| + | |||
| <ol type="a" start=3> | <ol type="a" start=3> | ||
| - | <li>$ \displaystyle \int_{1}^{2} \frac{4x^2 - 2}{3x} \, dx = \int_{1}^{2} \frac{2(2x^2-1)}{3x} \, dx = \frac{2}{3} \int_{1}^{2} \frac{2x^2 - 1}{x} \, dx = \frac{2}{3} \int_{1}^{2} \Bigl(2x - \frac{1}{x}\Bigr) \, dx$<br> | + | <li>$ \displaystyle \int_{1}^{2} \frac{4x^2 - 2}{3x} \, dx = \int_{1}^{2} \frac{2(2x^2-1)}{3x} \, dx = \frac{2}{3} \int_{1}^{2} \frac{2x^2 - 1}{x} \, dx = \frac{2}{3} \int_{1}^{2} \Bigl(2x - \frac{1}{x}\Bigr) \, dx\vphantom{\Biggl(}$<br> |
| $\displaystyle\phantom{\int_{1}^{2} \frac{4x^2 - 2}{3x} \, dx}{}= \frac{2}{3} \Bigl[\,x^2 - \ln x\,\Bigr]_{1}^{2} = \frac {2}{3}\Bigl((4- \ln 2) - (1 - \ln 1)\Bigr) = {\textstyle\frac{2}{3}}(3 - \ln 2) = 2 - {\textstyle\frac{2}{3}}\ln 2 $ <br><br> | $\displaystyle\phantom{\int_{1}^{2} \frac{4x^2 - 2}{3x} \, dx}{}= \frac{2}{3} \Bigl[\,x^2 - \ln x\,\Bigr]_{1}^{2} = \frac {2}{3}\Bigl((4- \ln 2) - (1 - \ln 1)\Bigr) = {\textstyle\frac{2}{3}}(3 - \ln 2) = 2 - {\textstyle\frac{2}{3}}\ln 2 $ <br><br> | ||
| </ol> | </ol> | ||
| Rad 312: | Rad 316: | ||
| ==Area mellan kurvor== | ==Area mellan kurvor== | ||
| - | Om $\,f(x) \ge g(x)\,$ i ett intervall gäller att arean mellan funktionskurvorna ges av | + | Om $\,f(x) \ge g(x)\,$ i ett intervall $\,a\le x\le b\,$ gäller att arean mellan funktionskurvorna ges av |
| $$\int_{a}^{b} f(x) \, dx - \int_{a}^{b} g(x) \, dx\,\mbox{,}$$ | $$\int_{a}^{b} f(x) \, dx - \int_{a}^{b} g(x) \, dx\,\mbox{,}$$ | ||
| vilket kan förenklas till | vilket kan förenklas till | ||
| Rad 348: | Rad 352: | ||
| [[Bild:Integral18.gif|150px|right]] | [[Bild:Integral18.gif|150px|right]] | ||
| Kurvorna skär varandra i punkter där deras ''y''-värden är lika | Kurvorna skär varandra i punkter där deras ''y''-värden är lika | ||
| - | $$\eqalign{&x^2 = x^{1/3} \quad \Leftrightarrow \quad x^6 = x \quad \Leftrightarrow \quad x(x^5 - 1) = 0\cr\quad \Leftrightarrow \quad x=0 \quad \text{eller} \quad x=1\,\mbox{.}$$ | + | $$\eqalign{&x^2 = x^{1/3} \quad \Leftrightarrow \quad x^6 = x \quad \Leftrightarrow \quad x(x^5 - 1) = 0\cr&\quad \Leftrightarrow \quad x=0 \quad \text{eller} \quad x=1\,\mbox{.}}$$ |
| Mellan $\,x=0\,$ och $\,x=1\,$ är $\,\sqrt[\scriptstyle 3]{x}>x^2\,$ så områdets area ges av | Mellan $\,x=0\,$ och $\,x=1\,$ är $\,\sqrt[\scriptstyle 3]{x}>x^2\,$ så områdets area ges av | ||
| $$\int_{0}^{1} \bigl( x^{1/3} - x^2 \bigr) \, dx = \Bigl[\,\frac{ x^{4/3}}{4/3} - \frac{x^3}{3}\,\Bigr]_{0}^{1} = \Bigl[\,\frac{3x^{4/3}}{4} - \frac{x^3}{3}\, \Bigr]_{0}^{1} = {\textstyle\frac{3}{4}} - {\textstyle\frac{1}{3}} - 0 = {\textstyle\frac{5}{12}}\ \text{a.e.}$$ | $$\int_{0}^{1} \bigl( x^{1/3} - x^2 \bigr) \, dx = \Bigl[\,\frac{ x^{4/3}}{4/3} - \frac{x^3}{3}\,\Bigr]_{0}^{1} = \Bigl[\,\frac{3x^{4/3}}{4} - \frac{x^3}{3}\, \Bigr]_{0}^{1} = {\textstyle\frac{3}{4}} - {\textstyle\frac{1}{3}} - 0 = {\textstyle\frac{5}{12}}\ \text{a.e.}$$ | ||
| Rad 361: | Rad 365: | ||
| <br> | <br> | ||
| [[Bild:Integral19.gif|200px|right]] | [[Bild:Integral19.gif|200px|right]] | ||
| - | I figuren till höger är de tre kurvorna skisserade och då ser vi att området måste delas upp i två delområden och den totala arean ges av integralerna | + | I figuren till höger är kurvan och de två linjerna skisserade och då ser vi att området kan delas upp i två delområden som var och en ligger mellan två funktionskurvor. Den totala arean är därför summan av integralerna |
| - | $$A_1 = \int_{a}^{b} (2 - \frac{1}{x^2}) \, dx\quad\text{och}\quad A_2 = \int_{b}^{c} (2- x) \, dx\,\mbox{.}$$ | + | $$A_1 = \int_{a}^{\,b} (2 - \frac{1}{x^2}) \, dx\quad\text{och}\quad A_2 = \int_{b}^{\,c} (2- x) \, dx\,\mbox{.}$$ |
| Vi bestämmer först skärningspunkterna $\,x=a\,$, $\,x=b\,$ och $\,x=c\,$: | Vi bestämmer först skärningspunkterna $\,x=a\,$, $\,x=b\,$ och $\,x=c\,$: | ||
| *Skärningspunkten $\,x=a\,$ bestäms av ekvationen | *Skärningspunkten $\,x=a\,$ bestäms av ekvationen | ||
| $$\frac{1}{x^2} = 2 \quad \Leftrightarrow \quad x^2 = \frac{1}{2} \quad \Leftrightarrow \quad x = \pm \frac{1}{\sqrt{2}}\,\mbox{.}$$ | $$\frac{1}{x^2} = 2 \quad \Leftrightarrow \quad x^2 = \frac{1}{2} \quad \Leftrightarrow \quad x = \pm \frac{1}{\sqrt{2}}\,\mbox{.}$$ | ||
| - | (Den negativa roten är dock inte aktuell.) | + | :(Den negativa roten är dock inte aktuell.) |
| *Skärningspunkt $\,x=b\,$ bestäms av ekvationen | *Skärningspunkt $\,x=b\,$ bestäms av ekvationen | ||
| Rad 375: | Rad 379: | ||
| Integralerna blir därför | Integralerna blir därför | ||
| - | $$\eqalign{A_1 &= \int_{1/\sqrt{2}}^{1} \Bigl(2 - \frac{1}{x^2}\Bigr) \, dx = \int_{1/\sqrt{2}}^{1} \bigl(2 - x ^{-2}\bigr) \, dx = \Bigl[\,2x-\frac{x^{-1}}{-1}\,\Bigr]_{1/\sqrt{2}}^{1} = \Bigl[\,2x + \frac{1}{x}\,\Bigr]_{1/\sqrt{2}}^{1}\cr &=(2+ 1) - \Bigl( \frac{2}{\sqrt{2}} + \sqrt{2}\Bigr) = 3 - 2\sqrt{2}\,\mbox{,}\cr A_2&= \int_{1}^{2} (2 - x) \, dx = \Bigl[\,2x - \frac{x^2}{2}\,\Bigr]_{1}^{2} = (4-2) - \Bigl(2- \frac{1}{2}\Bigr) = \frac{1}{2}\,\mbox{.}}$$ | + | $$\eqalign{A_1 &= \int_{1/\sqrt{2}}^{1} \Bigl(2 - \frac{1}{x^2}\Bigr) \, dx = \int_{1/\sqrt{2}}^{1} \bigl(2 - x ^{-2}\bigr) \, dx = \Bigl[\,2x-\frac{x^{-1}}{-1}\,\Bigr]_{1/\sqrt{2}}^{1} = \Bigl[\,2x + \frac{1}{x}\,\Bigr]_{1/\sqrt{2}}^{1}\cr &=(2+ 1) - \Bigl( \frac{2}{\sqrt{2}} + \sqrt{2}\,\Bigr) = 3 - 2\sqrt{2}\,\mbox{,}\cr A_2&= \int_{1}^{2} (2 - x) \, dx = \Bigl[\,2x - \frac{x^2}{2}\,\Bigr]_{1}^{2} = (4-2) - \Bigl(2- \frac{1}{2}\Bigr) = \frac{1}{2}\,\mbox{.}}$$ |
| Den sammanlagda arean blir | Den sammanlagda arean blir | ||
Nuvarande version
|
Innehåll:
Lärandemål: Efter detta avsnitt ska du ha lärt dig att:
|
||||
[redigera] Area under en funktionskurvaVi har tidigare sett att lutningen på en funktionskurva är intressant. Den ger oss information om hur funktionen ändras och har stor betydelse i många tillämpningar.
På ett liknande sätt är den area som bildas mellan en funktionskurva och x-axeln betydelsefull. Den är naturligtvis beroende av funktionskurvans utseende och därmed intimt besläktad med funktionen i fråga. Det är lätt att inse att denna area har en praktisk betydelse i många olika sammanhang. Den tillryggalagda sträckan är i respektive fall $$s(10)=5\cdot 10 = 50\,\mbox{m},\quad s(10)= 5\cdot4+5\cdot 6=50\,\mbox{m},\quad s(10)=\displaystyle\frac{5\cdot10}{2}=25\,\mbox{m}\,\mbox{.}$$ I samtliga fall ser man att föremålets tillryggalagda sträcka motsvaras av arean under funktionskurvan. Exempel 1 Anm: Eftersom arean kan approximeras med en (eller flera) rektangel så kan produkten av koordinataxlarnas enheter visa areans enhet och därmed ge en vink om vad arean symboliserar. Areans enhet:
[redigera] IntegralbeteckningenFör att beskriva arean under en funktionskurva i symbolform inför man integraltecknet $\,\int\,$ och gör följande definition: Med integralen av den positiva funktionen $\,f(x)\,$ från $\,a\,$ till $\,b\,$ menas arean mellan kurvan $\,y=f(x)\,$ och x-axeln från $\,x=a\,$ till $\,x=b\,$ , vilket med symboler skrivs $$\int_{a}^{\,b} f(x)\, dx\,\mbox{.}$$ Talen $\,a\,$ och $\,b\,$ kallas undre respektive övre integrationsgräns, $\,f(x)\,$ kallas integrand och $\,x\,$ integrationsvariabel. Exempel 2 Ur definitionen följer direkt att $$\int_{a}^{\,b} f(x)\, dx + \int_{b}^{\,c} f(x)\, dx = \int_{a}^{\,c} f(x)\, dx\,\mbox{.}$$
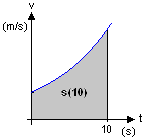
Exempel 3 För ett föremål, vars hastighet förändras enligt funktionen $\,v(t)\,$ kan den tillryggalagda sträckan efter 10 s beskrivas med integralen $$\int_{0}^{10} v(t)\, dt\,\mbox{.}$$
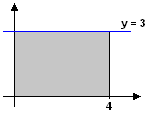
Exempel 4 Vatten rinner in i en tank med en hastighet som är $\,f(t)\,$ liter/s efter $\,t\,$ sekunder. Integralen $$\int_{9}^{10} f(t)\, dt$$ anger då hur många liter som rinner in i tanken under den tionde sekunden. Exempel 5 Beräkna integralerna
[redigera] Primitiv funktionFunktionen $\,F\,$ är en primitiv funktion till $\,f\,$ om $\,F'(x) = f(x)\,$ i något intervall. Om $\,F(x)\,$ är en primitiv funktion till $\,f(x)\,$ så är det klart att även $\,F(x) + C\,$ är det, för varje konstant $\,C\,$. Dessutom kan man visa att $\,F(x) + C\,$ beskriver samtliga primitiva funktioner till $\,f(x)\,$. Exempel 6
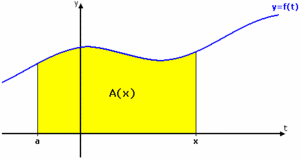
[redigera] Samband mellan integral och primitiv funktionVi har tidigare konstaterat att arean under en funktionskurva, dvs. integralen av en funktion, är beroende av funktionskurvans utseende. Det visar sig att detta beroende utnyttjar den primitiva funktionen, vilket också ger oss möjligheten att beräkna en sådan area exakt. Antag att $\,f\,$ är en kontinuerlig funktion på ett intervall (= funktionskurvan har inga avbrott i intervallet). Värdet av integralen $\ \int_{a}^{b} f(x) \, dx\ $ är då beroende av integrationsgränserna $\,a\,$ och $\,b\,$, men om man låter $\,a\,$ vara ett fixt värde och sätter $\,x\,$ som övre gräns blir integralens värde beroende enbart av den övre integrationsgränsen. För att tydliggöra detta använder vi här i stället $\,t\,$ som integrationsvariabel: $$A(x) = \int_{a}^{\,x} f(t) \, dt\,\mbox{.}$$
Om vi låter $\,h \rightarrow 0\,$ så går vänstra ledet mot $\,A'(x)\,$ och det högra ledet mot $\,f(x)\,$ , dvs. $$A'(x) = f(x)\,\mbox{.}$$ Funktionen $\,A(x)\,$ är alltså en primitiv funktion till $\,f(x)\,$. [redigera] Beräkning av integralerFör att kunna använda primitiva funktioner vid beräkning av en bestämd integral, noterar vi först att om $\,F\,$ är en primitiv funktion till $\,f\,$ så är $$\int_{a}^{\,b} f(t) \, dt = F(b) + C$$ där konstanten $\,C\,$ måste väljas så att högerledet blir noll när $\,b=a\,$, dvs. $$\int_{a}^{\,a} f(t) \, dt = F(a) + C = 0$$ vilket ger att $\,C=-F(a)\,$. Om vi sammanfattar har vi alltså att $$\int_{a}^{\,b} f(t) \, dt = F(b) - F(a)\,\mbox{.}$$ Vi kan naturligtvis här lika gärna välja $\,x\,$ som integrationsvariabel och skriva $$\int_{a}^{\,b} f(x) \, dx = F(b) - F(a)\,\mbox{.}$$ Vid beräkning av integraler utför man detta i två steg. Först bestämmer man en primitiv funktion och sedan sätter man in integrationsgränserna. Man skriver vanligtvis $$\int_{a}^{\,b} f(x) \, dx = \Bigl[\,F(x)\,\Bigr]_{a}^{b} = F(b) - F(a)\,\mbox{.}$$
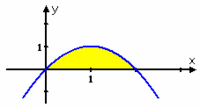
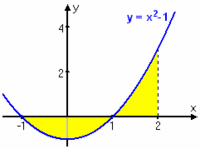
Exempel 7 Arean som begränsas av kurvan $\,y=2x - x^2\,$ och x-axeln kan beräknas med hjälp av integralen $$\int_{0}^{2} (2x-x^2) \, dx\,\mbox{.}$$ Eftersom $\,x^2-x^3/3\,$ är en primitiv funktion till integranden är integralens värde $$\int_{0}^{2} (2x-x^2) \, dx=\Bigl[\,x^2 - {\textstyle\frac{1}{3}}x^3\, \Bigr]_{0}^{2} = \bigl( 2^2 - {\textstyle\frac{1}{3}}2^3\bigr) - \bigl(0^2-{\textstyle\frac{1}{3}}0^3\bigr) = 4 - {\textstyle\frac{8}{3}} = {\textstyle\frac{4}{3}}\,\mbox{.}$$ Arean är $\,\frac{4}{3}\,$ a.e.
[redigera] BaklängesderiveringAtt derivera de vanliga funktionstyperna innebär inga oöverstigliga problem; det finns generella metoder för detta. Att utföra den omvända operationen, dvs. hitta en primitiv funktion till en given funktion är dock betydligt svårare och i vissa fall omöjligt! Det finns ingen systematisk metod som fungerar överallt, men genom att utnyttja de vanliga deriveringsreglerna "baklänges" och dessutom lära sig ett antal specialmetoder och knep kan man klara av en stor del av de funktioner som vanligtvis förekommer. Symbolen $\ \int f(x) \,dx\ $ kallas den obestämda integralen av $\,f(x)\,$ och används för att beteckna en godtycklig primitiv funktion till $\,f(x)\,$. De vanliga deriveringsreglerna ger att $$\eqalign{\int x^n \, dx &= \frac{x^{n+1}}{n+1} + C \quad \text{där }\ n \ne -1\cr \int x^{-1} \, dx &= \ln |x| + C\cr \int e^x \, dx &= e^x + C\cr \int \cos x \, dx &= \sin x + C\cr \int \sin x \, dx &= -\cos x + C}$$ Exempel 8
[redigera] Kompensation för ”inre derivata”Vid derivering av en sammansatt funktion använder man sig av kedjeregeln, som innebär att man multiplicerar med den inre derivatan. Om den inre funktionen då är linjär så blir den inre derivatan en konstant. Vid integrering av en sådan funktion måste man därför dividera med den inre derivatan för att kompensera för detta.
Exempel 9
Exempel 10
Observera att detta sätt att kompensera för den inre derivatan endast fungerar om den inre derivatan är en konstant. [redigera] Räkneregler för integralerMed hjälp av beräkningsformeln för integraler är det lätt att visa följande räkneregler för integraler:
Den sammanlagda arean blir $\qquad A_1 + A_2 = \displaystyle \int_{a}^{\,b} f(x)\, dx - \displaystyle \int_{b}^{\,c} f(x)\, dx\,$. Anm:
Exempel 11
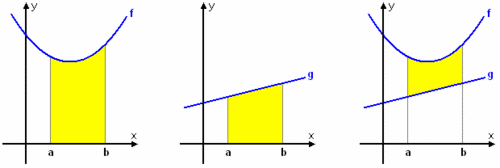
[redigera] Area mellan kurvorOm $\,f(x) \ge g(x)\,$ i ett intervall $\,a\le x\le b\,$ gäller att arean mellan funktionskurvorna ges av $$\int_{a}^{b} f(x) \, dx - \int_{a}^{b} g(x) \, dx\,\mbox{,}$$ vilket kan förenklas till $$\int_{a}^{b} (f(x) - g(x)) \, dx\,\mbox{.}$$
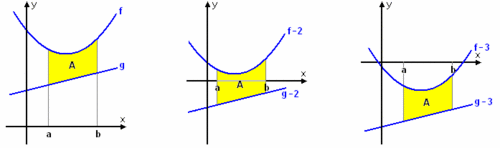
$$\eqalign{A &= \displaystyle\int_{a}^{b} \bigl(f(x)-g(x)\bigr)\,dx\cr A &= \int_{a}^{b} \bigl((f(x)-2) - (g(x)-2)\bigr)\,dx = \int_{a}^{b} \bigl(f(x)-g(x)\bigr)\,dx\cr A &= \int_{a}^{b} \bigl((f(x)-3) - (g(x)-3)\bigr)\,dx = \int_{a}^{b}\bigl(f(x)-g(x)\bigr)\,dx}$$
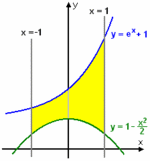
Exempel 12 Beräkna arean av det område som begränsas av kurvorna $\,y=e^x + 1\,$ och $\,y=1 - x^2/2\,$ samt linjerna $\,x = –1\,$ och $\,x = 1\,$.
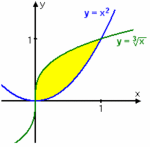
Exempel 13 Beräkna arean av det ändliga område som begränsas av kurvorna $\,y= x^2\,$ och $\,y= \sqrt[\scriptstyle 3]{x}\,$.
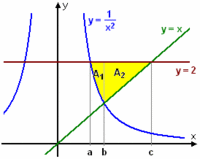
Kurvorna skär varandra i punkter där deras y-värden är lika $$\eqalign{&x^2 = x^{1/3} \quad \Leftrightarrow \quad x^6 = x \quad \Leftrightarrow \quad x(x^5 - 1) = 0\cr&\quad \Leftrightarrow \quad x=0 \quad \text{eller} \quad x=1\,\mbox{.}}$$ Mellan $\,x=0\,$ och $\,x=1\,$ är $\,\sqrt[\scriptstyle 3]{x}>x^2\,$ så områdets area ges av $$\int_{0}^{1} \bigl( x^{1/3} - x^2 \bigr) \, dx = \Bigl[\,\frac{ x^{4/3}}{4/3} - \frac{x^3}{3}\,\Bigr]_{0}^{1} = \Bigl[\,\frac{3x^{4/3}}{4} - \frac{x^3}{3}\, \Bigr]_{0}^{1} = {\textstyle\frac{3}{4}} - {\textstyle\frac{1}{3}} - 0 = {\textstyle\frac{5}{12}}\ \text{a.e.}$$ Exempel 14 Beräkna arean av det område som begränsas av kurvan $\,y= \displaystyle \frac{1}{x^2}\,$ samt linjerna $\,y=x\,$ och $\,y = 2\,$.
I figuren till höger är kurvan och de två linjerna skisserade och då ser vi att området kan delas upp i två delområden som var och en ligger mellan två funktionskurvor. Den totala arean är därför summan av integralerna $$A_1 = \int_{a}^{\,b} (2 - \frac{1}{x^2}) \, dx\quad\text{och}\quad A_2 = \int_{b}^{\,c} (2- x) \, dx\,\mbox{.}$$ Vi bestämmer först skärningspunkterna $\,x=a\,$, $\,x=b\,$ och $\,x=c\,$:
$$\frac{1}{x^2} = 2 \quad \Leftrightarrow \quad x^2 = \frac{1}{2} \quad \Leftrightarrow \quad x = \pm \frac{1}{\sqrt{2}}\,\mbox{.}$$
$$\frac{1}{x^2} = x \quad \Leftrightarrow \quad x^3 = 1 \quad \Leftrightarrow \quad x=1\,\mbox{.}$$
Integralerna blir därför $$\eqalign{A_1 &= \int_{1/\sqrt{2}}^{1} \Bigl(2 - \frac{1}{x^2}\Bigr) \, dx = \int_{1/\sqrt{2}}^{1} \bigl(2 - x ^{-2}\bigr) \, dx = \Bigl[\,2x-\frac{x^{-1}}{-1}\,\Bigr]_{1/\sqrt{2}}^{1} = \Bigl[\,2x + \frac{1}{x}\,\Bigr]_{1/\sqrt{2}}^{1}\cr &=(2+ 1) - \Bigl( \frac{2}{\sqrt{2}} + \sqrt{2}\,\Bigr) = 3 - 2\sqrt{2}\,\mbox{,}\cr A_2&= \int_{1}^{2} (2 - x) \, dx = \Bigl[\,2x - \frac{x^2}{2}\,\Bigr]_{1}^{2} = (4-2) - \Bigl(2- \frac{1}{2}\Bigr) = \frac{1}{2}\,\mbox{.}}$$ Den sammanlagda arean blir $$ A_1 + A_2 = 3 - 2\sqrt{2} + {\textstyle\frac{1}{2}} = {\textstyle\frac{7}{2}} - 2\sqrt{2}\ \text{a.e.}$$ |
|