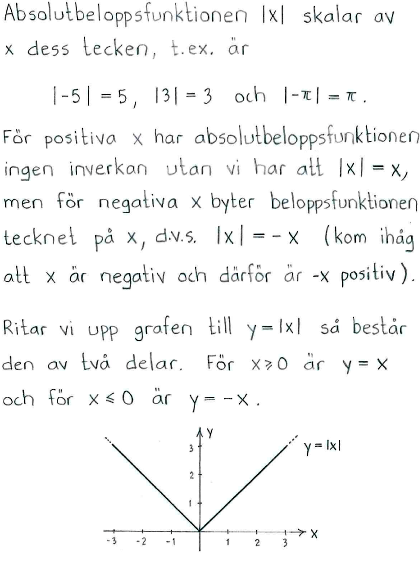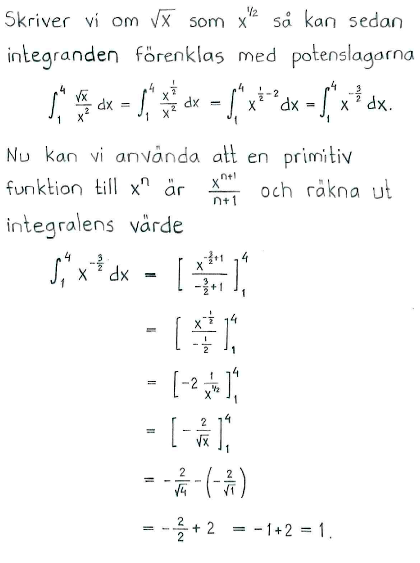2.1 Övningar
Sommarmatte 2
| Versionen från 19 juli 2007 kl. 09.08 (redigera) KTH.SE:u1zpa8nw (Diskussion | bidrag) (→Övning 2.1:2) ← Gå till föregående ändring |
Versionen från 19 juli 2007 kl. 09.08 (redigera) (ogör) KTH.SE:u1zpa8nw (Diskussion | bidrag) (→Övning 2.1:3) Gå till nästa ändring → |
||
| Rad 209: | Rad 209: | ||
| </tr> | </tr> | ||
| </table> | </table> | ||
| - | Ledning b) Använd att $\sin2v=2\sin v\cos v$<br\> | ||
| - | Ledning d) $\displaystyle\int\frac{x^2+1}{x}\, dx=\int\frac{x^2}{x}\, dx+\int\frac{1}{x}\, dx$ | ||
| </div> | </div> | ||
Versionen från 19 juli 2007 kl. 09.08
Innehåll |
Övning 2.1:1
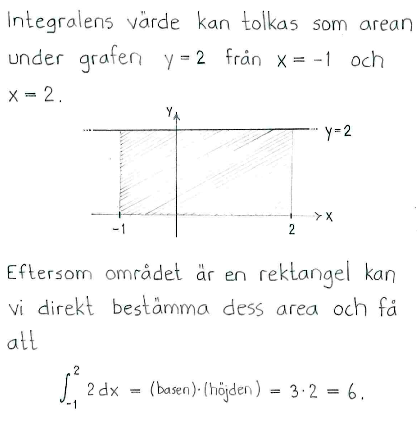
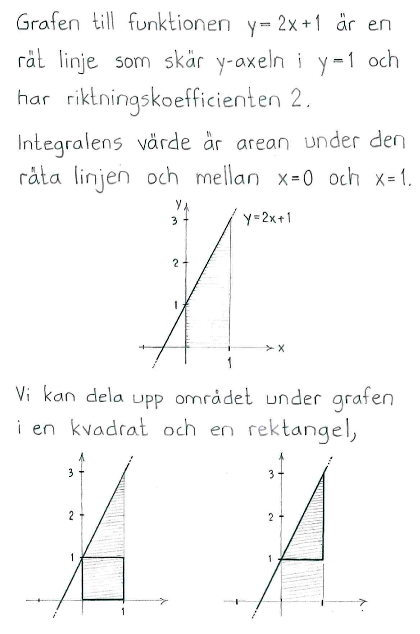
| a) | $\displaystyle\int_{-1}^{2} 2\, dx$ | b) | $\displaystyle\int_{0}^{1} (2x+1)\, dx$ |
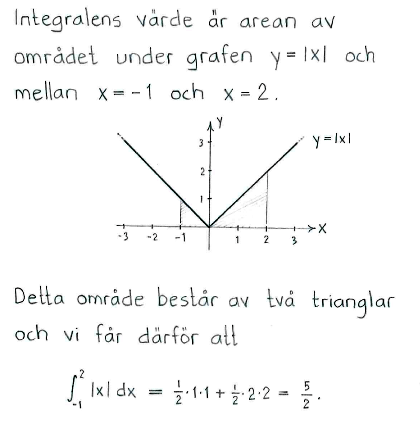
| c) | $\displaystyle \int_{0}^{2} (3-2x)\, dx$ | d) | $\displaystyle\int_{-1}^{2}|x| \, dx$ |
| a) | $6$ | b) | $2$ |
| c) | $2$ | d) | $\displaystyle\frac{5}{2}$ |
Lösning till delfråga a
|
|
Lösning till delfråga b
|
|
Lösning till delfråga c
|
|
|
Lösning till delfråga d |
Övning 2.1:2
| a) | $\displaystyle\int_{0}^{2} (x^2+3x^3)\, dx$ | b) | $\displaystyle\int_{-1}^{2} (x-2)(x+1)\, dx$ |
| c) | $ \displaystyle\int_{4}^{9} \left(\sqrt{x} - \displaystyle\frac{1}{\sqrt{x}}\right)\, dx$ | d) | $\displaystyle\int_{1}^{4} \displaystyle\frac{\sqrt{x}}{x^2}\, dx$ |
Facit till alla delfrågor
| a) | $\displaystyle\frac{44}{3}$ | b) | $\displaystyle-\frac{9}{2}$ |
| c) | $\displaystyle\frac{32}{3}$ | d) | $1$ |
Lösning till delfråga a
|
|
Lösning till delfråga b
|
|
Lösning till delfråga c
|
|
Lösning till delfråga d
|
|
Övning 2.1:3
| a) | $\displaystyle\int \sin x\, dx$ | b) | $\displaystyle\int 2\sin x \cos x\, dx$ |
| c) | $ \displaystyle\int e^{2x}(e^x+1)\, dx$ | d) | $\displaystyle\int \displaystyle\frac{x^2+1}{x}\, dx$ |
Facit till alla delfrågor
| a) | $-\cos x + C$ | b) | $\displaystyle-\frac{\cos 2x}{2}+C$ |
| c) | $\displaystyle\frac{e^{3x}}{3}+\frac{e^{2x}}{2}+C$ | d) | $\displaystyle\frac{x^2}{2}+\ln x + C$ |
Övning 2.1:4
| a) | Beräkna arean mellan kurvan $y=\sin x$ och $x$-axeln när $0\le x \le \frac{5\pi}{4}$ |
| b) | Beräkna arean av det område under kurvan $y=-x^2+2x+2$ och ovanför $x$-axeln |
| c) | Beräkna arean av det ändliga området mellan kurvorna $y=\frac{1}{4}x^2+2$ och $y=8-\frac{1}{8}x^2$ (studentexamen 1965). |
| d) | Beräkna arean av det ändliga området som kurvorna $y=x+2, y=1$ och $y=\frac{1}{x}$ innesluter. |
| e) | Beräkna arean av området som ges av olikheterna $x^2\le y\le x+2$. |
Facit till alla delfrågor
| a) $3-\displaystyle\frac{1}{\sqrt2}$ a.e. |
| b) $\displaystyle 4.\sqrt{3}$ a.e. |
| c) $32$ a.e. |
| d) $\sqrt{2}-1-\ln(\sqrt{2}-1)\,$ a.e. |
| e) $\displaystyle\frac{9}{2}$ a.e. |
Lösning till delfråga b
Det första som vi behöver göra är att ta reda på var kurvan $y = -x^2+2x+2$ skär x-axeln, så vi sätter $y=0$ och löser andragradsekvationen;
$$-x^2+2x+2 = 0 \Rightarrow$$ $$ x^2-2x-2 = 0 \Rightarrow $$ $$ x = 1 \pm \sqrt{1+2} \Rightarrow$$ $$x_1 = 1-\sqrt{3} \qquad x_2 = 1+\sqrt{3} $$
Vi kan försäkra oss om att kurvan ligger ovanför x-axeln mellan dessa punkter, eftersom t.ex. punkten $x=0$ ger ett positivt värde. Vi kan nu ställa upp integralen som
$$ \int_{1-\sqrt{3}}^{1+\sqrt{3}} -x^2 + 2x +2 dx $$
De primitiva funktionerna till $-x^2$, $2x$ och $2$ är $-\frac{x^3}{3}$, $x^2$ resp. $2x$, så vi får
$$ \left[ -\frac{x^3}{3} + x^2 + 2x \right]_{1-\sqrt{3}}^{1+\sqrt{3}} = \left[ x( x + 2 - \frac{x^2}{3} ) \right]_{1-\sqrt{3}}^{1+\sqrt{3}} $$
Nu är det bara att sätta in gränserna och vi får det enorma uttrycket
$$ (1+\sqrt{3})( (1+\sqrt{3}) + 2 - \frac{(1+\sqrt{3})^2}{3} ) - (1-\sqrt{3})( (1-\sqrt{3}) + 2 - \frac{(1-\sqrt{3})^2}{3} ) $$
För att inte tappa bort oss, så räknar vi ut de olika termerna var för sig.
Vänstra uttrycket blir;
$$ (1+\sqrt{3})( (1+\sqrt{3}) + 2 - \frac{(1+\sqrt{3})^2}{3} ) = $$ $$ (1+\sqrt{3})( 3+\sqrt{3} - \frac{1+2\sqrt{3}+3}{3} ) = $$ $$ (1+\sqrt{3})( 3+\sqrt{3} - \frac{4}{3} - \frac{2\sqrt{3}}{3} ) = $$ $$ (1+\sqrt{3})( \frac{5}{3} + \frac{\sqrt{3}}{3} ) = $$ $$ \frac{5}{3} + \frac{\sqrt{3}}{3} + \frac{5\sqrt{3}}{3} + \frac{\sqrt{3}^2}{3} = $$ $$ \frac{8}{3} + 2\sqrt{3} $$
Högra uttrycket räknas ut på nästan samma sätt;
$$ (1-\sqrt{3})( (1-\sqrt{3}) + 2 - \frac{(1-\sqrt{3})^2}{3} ) = $$ $$ (1-\sqrt{3})( 3-\sqrt{3} - \frac{1-2\sqrt{3}+3}{3} ) = $$ $$ (1-\sqrt{3})( 3-\sqrt{3} - \frac{4}{3} + \frac{2\sqrt{3}}{3} ) = $$ $$ (1-\sqrt{3})( \frac{5}{3} - \frac{\sqrt{3}}{3} ) = $$ $$ \frac{5}{3} - \frac{\sqrt{3}}{3} - \frac{5\sqrt{3}}{3} + \frac{\sqrt{3}^2}{3} = $$ $$ \frac{8}{3} - 2\sqrt{3} $$
Sammanlagt får vi då $\displaystyle{ (\frac{8}{3} + 2\sqrt{3})-(\frac{8}{3} - 2\sqrt{3}) = 4\sqrt{3} }$.
Svaret på uppgiften är alltså $\displaystyle{ 4.\sqrt{3} }$ a.e.
Övning 2.1:5
Beräkna integralerna
| a) | $\displaystyle \int \displaystyle\frac{dx}{\sqrt{x+9}-\sqrt{x}}\quad$ (Ledning: förläng med nämnarens konjugat) |
| b) | $\displaystyle \int \sin^2 x\quad$ (Ledning: skriv om integranden med en trigonometrisk formel) |
Facit till alla delfrågor
| a) $\displaystyle\frac{2}{27}\left((x+9)\sqrt{x+9}+x\sqrt{x}\right)+C$ |
| b) $-\displaystyle\frac{\sin2x}{4}+\frac{x}{2}+C$ |
