Deriveringsregler
Med hjälpa av derivatans definition kan man besätmma derivatan för de vanliga funktionstyperna.
Exempel 1
Om $f(x)=x^2$ så får vi enligt definitionen av derivata ändringskvoten
$$\frac{(x+h)^2-x^2}{h}=\frac{x^2+2hx+h^2-x^2}{h} = \frac{h(2x+h)}{h} = 2x + h $$
Om vi sedan låter $h$ bli noll så ser vi att lutningen i punkten blir $2x$. Vi har därmed visat att lutningen i en godtycklig punkt på kurvan $y=x^2$ är $2x$, dvs. derivatan av $x^2$ är $2x$.
På liknande sätt kan man härleda allmämnna deriveringsregler:
| Funktion
| Derivata
|
| $$x^n$$
| $$n \cdot x^{n-1}$$
|
| $$\ln x$$
| $$ \frac{1}{x}$$
|
| $$e^x$$
| $$e^x$$
|
| $$\sin x$$
| $$\cos x$$
|
| $$\tan x$$
| $$\frac{1}{\cos^2 x}$$
|
Dessutom gäller för summor och differenser av funktionsuttryck att
$$D(f(x) +g(x))= f'(x) + g'(x)$$
Samt, om $k$ är en konstant, att
$$D(k \cdot f(x)) = k \cdot f'(x)$$
Exempel 2
- $D(2x^3 - 4x + 10 - \sin x) = 6x^2 - 4 - \cos x$
- $ y= 3 \ln x + 3e^x \quad \rightarrow \quad y'= 3 \cdot \displaystyle\frac{1}{x} + 2 e^x = \displaystyle\frac{3}{x} + 2 e^x$
- $\displaystyle \frac{d}{dx}\left(\displaystyle\frac{3x^2}{5} - \displaystyle\frac{x^3}{2}\right) = \displaystyle\frac{d}{dx}\left(\frac{3}{5}x^2 - \displaystyle\frac{1}{2}x^3\right)= \displaystyle\frac{6}{5}x - \displaystyle\frac{3}{2}x^2= \frac{6x}{5} - \displaystyle\frac{3x^2}{2}$
- $ s(t)= v_0t + \displaystyle\frac{at^2}{2} \quad \rightarrow \quad s'(t)=v_0 + \displaystyle\frac{2at}{2} = v_0 + at$
Exempel 3
- $f(x) = \displaystyle\frac{1}{x} = x^{-1} \quad \rightarrow \quad f'(x) = -1 \cdot x^{-2} = -\displaystyle\frac{1}{x^2}$
- $f(x)= \displaystyle\frac{1}{3x^2} = \displaystyle\frac{1}{3} \cdot x^{-2} \quad \rightarrow \quad f'(x) = -\displaystyle\frac{2}{3} \cdot x^{-3} = -\displaystyle\frac{2}{3x^3} $
- $g(t) = \displaystyle \frac{t^2 - 2t + 1}{t} = t -2 + \displaystyle\frac{1}{t} \quad \rightarrow \quad g'(t) = 1 - \displaystyle\frac{1}{t^2}$
- $y = \left( x^2 + \displaystyle\frac{1}{x} \right)^2 = x^4 + 2 \cdot x^2 \cdot \displaystyle\frac{1}{x} + \left(\displaystyle\frac{1}{x} \right)^2 = x^4 + 2x + x^{-2} \quad \rightarrow \quad$
$\quad \rightarrow \quad y' =4x^3 + 2 -2x^{-3} = 4x^3 + 2 - \displaystyle\frac{2}{x^3}$
Exempel 4
$f(x)=x^2 + x^{-2} \quad \rightarrow \quad f'(x) = 2x -2x^{-3} = 2x - \displaystyle \frac{2}{x^3}$
$ f '(2) = 2\cdot 2 - \displaystyle \frac{2}{2^3}= 4- \displaystyle \frac{1}{4} = \displaystyle \frac{15}{4}$
$ f '(-1) = 2 \cdot (-1) - \displaystyle \frac{2}{(-1)^3} = -2 + 2 = 0$
$ f '(0) =$ ej def.
Exempel 5
Ett föremål rör sig enligt $s(t) = t^3 -4t^2 +5t$ , där $s$ km är avståndet från startpunkten efter $t$ timmar.
Beräkna $s'(3)$ och förklara vad värdet står för.
Lösning
$ s'(t) = 3t^2 - 8t +5 $
$ s'(3) = 3 \cdot 3^2 - 8 \cdot 3 + 5 = 8$
Efter 3 timmar är föremålets hastighet 8 km/h.
Exempel 6
Totalkostnaden $T$ kr för tillverkning av x gummidräkter ges av funktionen
$$ T(x) = 40000 + 370x -0,09x^2 \quad (0 \le x \le 200)$$
Beräkna och förklara
- $T(120)$
- $T'(120)$
Lösning
- $T(120)=40000 + 370 \cdot 120 - 0,09 \cdot 120^2 = 83104$
Totalkostnaden för att tillverka 120 gummidräkter är 83104 kr.
- $T'(x)= 370 - 0,18x$
$T'(120) = 370 - 0,18 \cdot 120 \approx 348$
Marginalkostnaden ("kostnaden för att tillverka ytterligare 1 enhet") vid 120 tillverkade gummidräkter är 348 kr.
Tangenter och normaler
En tangent till en kurva är en rät linje som tangerar kurvan, dvs. som endast har en punkt gemensam med kurvan – tangeringspunkten.
En normal till en kurva är en rät linje som är vinkelrät mot kurvan i en viss punkt på kurvan (och därmed också vinkelrät mot kurvans tangent i denna punkt).
För vinkelräta linjer gäller att produkten av deras riktningskoefficienter är $–1$, dvs. om tangentens riktningskoefficient betecknas $k_T$ och normalens $k_N$ så är $k_T \cdot k_N = -1$. Eftersom vi kan bestämma lutningen på en kurva med hjälp av derivatan så kan vi också bestämma ekvationen för en tangent eller normal om vi känner till funktionsuttrycket för kurvan.
Exempel 7
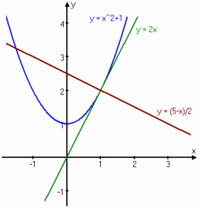
Bestäm ekvationen för tangenten respektive normalen till kurvan $y=x^2 + 1$ i punkten $(1,2)$
Lösning
Tangentens ekvation är $y = kx + m$ , där $k= y'(1)$.
$y' = 2x \quad , \quad y'(1) = 2\cdot 1 = 2$
Eftersom linjen också passerar punkten $(1,2)$ har vi att
$2 = 2 \cdot 1 + m \quad \rightarrow \quad m = 0 $
Tangentens ekvation är alltså $y=2x$
Riktningskoefficienten för normalen är $k_N = -\displaystyle \frac{1}{k_T} = \displaystyle \frac{1}{2}$ .
Normalen går också genom punkten $(1, 2)$ , dvs.
$2= -\displaystyle \frac{1}{2}\cdot 1 + m \quad \rightarrow \quad m = \displaystyle \frac{5}{2} $
Normalen har ekvationen $y= -\displaystyle \frac{x}{2} + \displaystyle \frac{5}{2} = \displaystyle \frac{5-x}{2}$
Exempel 8
Kurvan $y = 2 \, e^x - 3x$ har en tangent vars riktningskoefficient är $–1$. Bestäm tangeringspunkten.
Lösning
$y' = 2 \, e^x -3$
$ y' = -1 \quad \rightarrow \quad 2 \, e^x = 2 \quad \rightarrow \quad x=0$
$ y(0) = 2 \, e^0 - 3 \cdot 0 = 2 $
Tangeringspunkten är (0, 2)
Derivering av produkt och kvot
Med hjälp av derivatans definition kan man också härleda deriveringsregler för produkter och kvoter av funktionsuttryck:
Deriveringsregler för produkter och kvoter:
$$D \left(f(x) \cdot g(x) \right) = f'(x) \cdot g(x) + f(x) \cdot g'(x)$$
$$ D \left( \frac{f(x)}{g(x)} \right) = \frac{f'(x) \cdot g(x) + f(x) \cdot g'(x)}{\left( g(x)\right)^2}$$
(Observera att derivering av produkter och kvoter inte är så enkelt som derivering av summor och differenser, där man kan derivera funktionsuttrycken termvis, dvs. var för sig!)
Exempel 9
- $ D(x^2 e^x) = 2xe^x + x^2e^x = e^x(2x +x^2)$
- $ D(x \sin x) = 1\cdot \sin x + x \cos x = \sin x + x \cos x$
- $ D(x \ln x -x) = 1 \cdot \ln x + x\cdot \displaystyle \frac{1}{x} - 1 = \ln x + 1 -1 = \ln x$
- $ D \tan x = D \displaystyle \frac{\sin x}{\cos x} = \displaystyle \frac{ \cos x \cdot \cos x - \sin x \cdot (-\sin x)}{(\cos x)^2} = \displaystyle \frac{\cos^2 x + \sin^2 x }{ \cos^2 x} = \displaystyle \frac{1}{\cos x}$
- $ D \displaystyle \frac{1+x}{\sqrt{x}} = \displaystyle \frac{ 1 \cdot \sqrt{x} - (1+x) \cdot \displaystyle \frac{1}{2\sqrt{x}}}{(\sqrt{x})^2} = \displaystyle \frac{ \displaystyle \frac{2x}{2\sqrt{x}} - \displaystyle \frac{1}{2\sqrt{x}} - \displaystyle \frac{x}{2\sqrt{x}}}{x} = \displaystyle \frac { \displaystyle \frac {x-1}{2\sqrt{x}}}{x} = \displaystyle \frac{x-1}{2x\sqrt{x}} $
- $ D \displaystyle \frac{ x e^x}{1+x} = \displaystyle \frac{ (1\cdot e^x + x\cdot e^x)(1+x) - x e^x \cdot 1}{(1+x)^2} = \displaystyle \frac{ e^x + x e^x + x e^x + x^2 e^x - x e^x}{ (1+x)^2} = \displaystyle \frac{ e^x(1 + x + x^2)} { (1+x)^2}$
Derivering av sammansatta funktioner
En funktion $y=f(g)$ där variabeln $g$ i sin tur är beroende av en variabel $x$ får formen $y=f \left( g(x) \right)$ och kallas sammansatt funktion.
Om man deriverar en sammansatt funktion med avseende på den oberoende variabeln x, använder man följande regel:
$$y'(x) = f'\left( g(x) \right) \cdot g'(x)$$
Denna regel brukar kallas kedjeregeln och kan beroende på val av symboler skrivas på olika sätt. Om vi i ovanstående t.ex. sätter $y=g(u)$ och $u=g(x)$ kan kedjeregeln skrivas
$$ \displaystyle \frac{dy}{dx} = \displaystyle \frac{dy}{du} \cdot \displaystyle \frac{du}{dx}$$
Man brukar säga att den sammansatta funktionen $y$ består av den yttre funktionen $f$ och den inre funktionen $g$. Analogt kallas $f'$ för den yttre derivatan och $g'$ den inre derivatan.
Exempel 10
För funktionen $y=(x^2 + 2x)^4$ är
| $y=u^4$
| yttre funktionen, och
|
| $u=x^2 + 2x$
| inre funktion.
|
| $\displaystyle \frac{dy}{du} = 4 u^3$
| är yttre derivatan, och
|
| $\displaystyle \frac{du}{dx} = 2x + 2$
| inre derivatan.
|
Derivatan av funktionen $y$ med avseende på $x$ blir enligt kedjeregeln
$$ \displaystyle \frac{dy}{dx} = \displaystyle \frac{dy}{du} \cdot \displaystyle \frac{du}{dx} = 4 u^3 \cdot (2x +2) = 4(x^2 + 2x)^3 \cdot (2x +2)$$
När man vant sig vid kedjeregeln inför man sällan nya beteckningar för yttre och inre funktion, utan man lär sig känna igen dessa och deriverar ”rakt på”, enligt mönstret
$$(yttre \, derivata)\cdot (inre \, derivata)$$
Kom ihåg att även använda produkt- eller kvotregeln när detta är nödvändigt.
Exempel 11
- $ f(x) = \sin (3x + 1)$
Yttre derivatan: $ \quad \cos (3x^2 +1)$
Inre derivatan: $ \quad 6x$
$f'(x) = \cos (3x^2 + 1) \cdot 6x = 6x \cos (3x +1)$
- $ y = 5 \, e^{x^2}$
Yttre derivatan: $ \quad 5 \, e^{x^2} $
Inre derivatan: $ \quad 2x$
$y' = 5 \, e^{x^2} \cdot 2x = 10x\, e^{x^2}$
- $ f(x) = e^{x\cdot \sin x}$
Yttre derivatan: $ \quad e^{x\cdot \sin x}$
Inre derivatan: $ \quad 1\cdot \sin x + x \cos x$
$f'(x) = e^{x\cdot \sin x} (\sin x + x \cos x)$
- $ s(t) = t^2 \cos (\ln t) $
$ s'(t) = 2t \cdot \cos (\ln t) + t^2 \cdot (-\sin (\ln t) \cdot \displaystyle \frac{1}{t} = 2t \cos (\ln t) - t \sin (\ln t)$
- $ D a^x = D \left( e^{\ln a} \right)^x = D e^{\ln a \cdot x} = e^{\ln a \cdot x} \cdot \ln a = a^x \cdot \ln a $
- $ D x^a = D \left( e^{\ln x} \right)^a = D e^{ a \cdot \ln x } = e^{a \cdot \ln x} \cdot a \cdot \displaystyle \frac{1}{x} = x^a \cdot a \cdot x^{-1} = ax^{a-1}$
Kedjeregeln kan även användas upprepade gånger på en funktion som är sammansatt i flera steg. Exempelvis funktionen $y= f \left ( g(h(x))\right)$ har derivatan
$$y'= f' \left ( g(h(x))\right) \cdot g'(h(x)) \cdot h´(x)$$
Exempel 12
- $ D(\sin^3 2x) = D (\sin 2x)^3 = 3(\sin 2x)^2 \cdot \cos 2x \cdot 2 = 6 \sin^2 2x \cos 2x $
- $ D \left(\sin (x^2 -3x)^4 \right) = \cos (x^2 -3x)^4 \cdot 4 (x^2 -3x)^3 \cdot (2x-3) $
- $ D \left(\sin^4 (x^2 -3x) \right) = D \left( \sin (x^2 -3x) \right)^4 = 4 \sin^3 (x^2 - 3x) \cdot \cos (x^2 -3x) \cdot (2x-3)$
- $ D \left ( e^{\sqrt{x^3-1}}\right) = e^{\sqrt{x^3-1}} \cdot \displaystyle \frac{1} {2 \sqrt{x^3-1}} \cdot 3 x^2 = \displaystyle \frac { 3 x^2 e^{\sqrt{x^3-1}}} {2 \sqrt{x^3-1}}$
Derivator av högre ordningar
Om en funktion är deriverbar mer än en gång så pratar man om funktionens andra-, tredjederivata, osv.
Andraderivatan brukar betecknas $f{'}{'}$ (läses ”f-biss”), medan tredje-, fjärdederivatan, etc, betecknas $f^{(3)} \, , \, f^{(4)}$ osv.
Även beteckningarna $D^2 f$ , $D^3 f$ ,... och $\displaystyle \frac{d^2 y}{dx^2}$ , $\displaystyle \frac{d^3 y}{dx^3}$, ... är vanliga.
Exempel 13
- $ f(x) = 3 e^{(x^2 -1)}$
$ f'(x) = 3 e^{(x^2 -1)} \cdot 2x = 6x e^{(x^2 -1)}$
$ f{'}{'}(x) = 6 e^{(x^2 -1)} + 6x e^{(x^2 -1)} \cdot 2x = 6 e^{(x^2 -1)} (1+ 2x^2) $
- $ y = \sin x \cos x$
$ \displaystyle \frac{dy}{dx} = \cos x \cos x + \sin x (- \sin x) = \cos^2 x - \sin^2 x$
$\displaystyle \frac{d^2 y}{dx^2} = 2 \cos x (-\sin x) - 2 \sin x \cos x = -4 \sin x \cos x $
- $ D ( e^x \sin x) = e^x \sin x + e^x \cos x = e^x (\sin x + \cos x)$
$ D^2 ( e^x \sin x) = D (e^x (\sin x + \cos x)) = $
$=e^x (\sin x + \cos x) + e^x (\cos x - \sin x) + e^x (\cos x - \sin x) = 2 e^x \cos x$
$D^3 ( e^x \sin x) = D (2 e^x \cos x) = 2 e^x \cos x + 2 e^x (-\sin x) = 2 e^x ( \cos x - \sin x )$
|