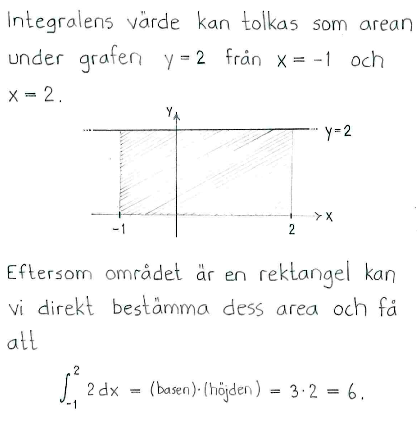
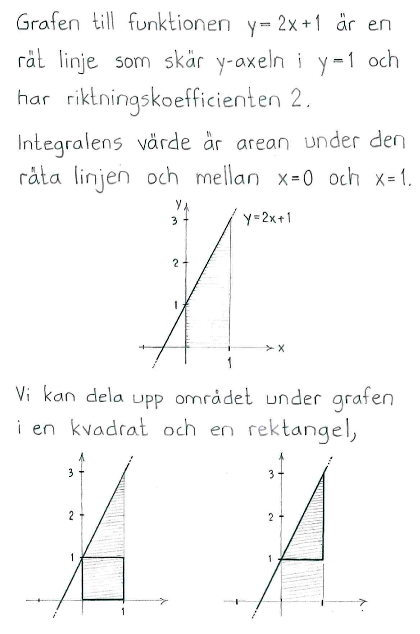
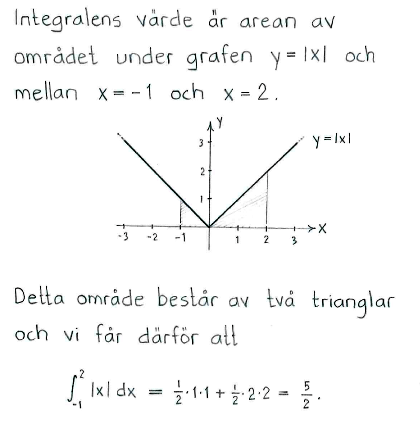
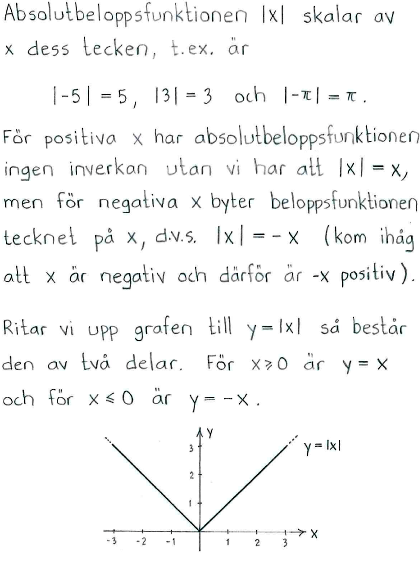2.1 Övningar

Sommarmatte 2

Hoppa till: navigering, sök

Innehåll

Övning 2.1:1

Tolka integralerna som areor och bestäm deras värde
a) $\displaystyle\int_{-1}^{2} 2\, dx$ b) $\displaystyle\int_{0}^{1} (2x+1)\, dx$
c) $\displaystyle \int_{0}^{2} (3-2x)\, dx$ d) $\displaystyle\int_{-1}^{2}|x| \, dx$

Ledning d) För $a < b < 0$ gäller $\displaystyle\int_{a}^{b}|x|\, dx=\int_{a}^{b} -x\,dx$


Facit 

Facit till alla delfrågor

a) $6$ b) $2$
c) $2$ d) $\displaystyle\frac{5}{2}$
Lösning a 
Den här artikeln är hämtad från http://wiki.math.se/wikis/sf0601_0701/index.php/2.1_%C3%96vningar

Lösning till delfråga a
Bild:2_1_1a.gif </div> </div>

Lösning b 

Lösning till delfråga b
Bild:2_1_1b-1(2).gif
Bild:2_1_1b-2(2).gif

Lösning c 

Lösning till delfråga c
Bild:2_1_1c-1(2).gif
Bild:2_1_1c-2(2).gif

Lösning d 

Lösning till delfråga d
Bild:2_1_1d-1(2).gif
Bild:2_1_1d-2(2).gif

Övning 2.1:2

Beräkna integralerna
a) $\displaystyle\int_{0}^{2} (x^2+3x^3)\, dx$ b) $\displaystyle\int_{-1}^{2} (x-2)(x+1)\, dx$
c) $ \displaystyle\int_{4}^{9} \left(\sqrt{x} - \displaystyle\frac{1}{\sqrt{x}}\right)\, dx$ d) $\displaystyle\int_{1}^{4} \displaystyle\frac{\sqrt{x}}{x^2}\, dx$

Ledning c,d) skriv om $\sqrt x=x^{1/2}$, och använd eventuellt potenslagarna.


Facit 

Facit till alla delfrågor

a) $\displaystyle\frac{44}{3}$ b) $\displaystyle-\frac{9}{2}$
c) $\displaystyle\frac{32}{3}$ d) $1$

Övning 2.1:3

Beräkna integralerna
a) $\displaystyle\int \sin x\, dx$ b) $\displaystyle\int 2\sin x \cos x\, dx$
c) $ \displaystyle\int e^{2x}(e^x+1)\, dx$ d) $\displaystyle\int \displaystyle\frac{x^2+1}{x}\, dx$

Ledning b) Använd att $\sin2v=2\sin v\cos v$
Ledning d) $\displaystyle\int\frac{x^2+1}{x}\, dx=\int\frac{x^2}{x}\, dx+\int\frac{1}{x}\, dx$


Facit 

Facit till alla delfrågor

a) $-\cos x + C$ b) $\displaystyle-\frac{\cos 2x}{2}+C$
c) $\displaystyle\frac{e^{3x}}{3}+\frac{e^{2x}}{2}+C$ d) $\displaystyle\frac{x^2}{2}+\ln x + C$

Övning 2.1:4

a) Beräkna arean mellan kurvan $y=\sin x$ och $x$-axeln när $0\le x \le \frac{5\pi}{4}$
b) Beräkna arean av det område under kurvan $y=-x^2+2x+2$ och ovanför $x$-axeln
c) Beräkna arean av det ändliga området mellan kurvorna $y=\frac{1}{4}x^2+2$ och $y=8-\frac{1}{8}x^2$ (studentexamen 1965).
d) Beräkna arean av det ändliga området som kurvorna $y=x+2, y=1$ och $y=\frac{1}{x}$ innesluter.
e) Beräkna arean av området som ges av olikheterna $x^2\le y\le x+2$.


Facit 

Facit till alla delfrågor

a)     $3-\displaystyle\frac{1}{\sqrt2}$ a.e.
b)     $\displaystyle 4.\sqrt{3}$ a.e.
c)     $32$ a.e.
d)     $\sqrt{2}-1-\ln(\sqrt{2}-1)\,$ a.e.
e)     $\displaystyle\frac{9}{2}$ a.e.


Lösning b 

Lösning till delfråga b

Det första som vi behöver göra är att ta reda på var kurvan $y = -x^2+2x+2$ skär x-axeln, så vi sätter $y=0$ och löser andragradsekvationen;

$$-x^2+2x+2 = 0 \Rightarrow$$ $$ x^2-2x-2 = 0 \Rightarrow $$ $$ x = 1 \pm \sqrt{1+2} \Rightarrow$$ $$x_1 = 1-\sqrt{3} \qquad x_2 = 1+\sqrt{3} $$

Vi kan försäkra oss om att kurvan ligger ovanför x-axeln mellan dessa punkter, eftersom t.ex. punkten $x=0$ ger ett positivt värde. Vi kan nu ställa upp integralen som

$$ \int_{1-\sqrt{3}}^{1+\sqrt{3}} -x^2 + 2x +2 dx $$

De primitiva funktionerna till $-x^2$, $2x$ och $2$ är $-\frac{x^3}{3}$, $x^2$ resp. $2x$, så vi får

$$ \left[ -\frac{x^3}{3} + x^2 + 2x \right]_{1-\sqrt{3}}^{1+\sqrt{3}} = \left[ x( x + 2 - \frac{x^2}{3} ) \right]_{1-\sqrt{3}}^{1+\sqrt{3}} $$


Nu är det bara att sätta in gränserna och vi får det enorma uttrycket

$$ (1+\sqrt{3})( (1+\sqrt{3}) + 2 - \frac{(1+\sqrt{3})^2}{3} ) - (1-\sqrt{3})( (1-\sqrt{3}) + 2 - \frac{(1-\sqrt{3})^2}{3} ) $$

För att inte tappa bort oss, så räknar vi ut de olika termerna var för sig.

Vänstra uttrycket blir;

$$ (1+\sqrt{3})( (1+\sqrt{3}) + 2 - \frac{(1+\sqrt{3})^2}{3} ) = $$ $$ (1+\sqrt{3})( 3+\sqrt{3} - \frac{1+2\sqrt{3}+3}{3} ) = $$ $$ (1+\sqrt{3})( 3+\sqrt{3} - \frac{4}{3} - \frac{2\sqrt{3}}{3} ) = $$ $$ (1+\sqrt{3})( \frac{5}{3} + \frac{\sqrt{3}}{3} ) = $$ $$ \frac{5}{3} + \frac{\sqrt{3}}{3} + \frac{5\sqrt{3}}{3} + \frac{\sqrt{3}^2}{3} = $$ $$ \frac{8}{3} + 2\sqrt{3} $$


Högra uttrycket räknas ut på nästan samma sätt;

$$ (1-\sqrt{3})( (1-\sqrt{3}) + 2 - \frac{(1-\sqrt{3})^2}{3} ) = $$ $$ (1-\sqrt{3})( 3-\sqrt{3} - \frac{1-2\sqrt{3}+3}{3} ) = $$ $$ (1-\sqrt{3})( 3-\sqrt{3} - \frac{4}{3} + \frac{2\sqrt{3}}{3} ) = $$ $$ (1-\sqrt{3})( \frac{5}{3} - \frac{\sqrt{3}}{3} ) = $$ $$ \frac{5}{3} - \frac{\sqrt{3}}{3} - \frac{5\sqrt{3}}{3} + \frac{\sqrt{3}^2}{3} = $$ $$ \frac{8}{3} - 2\sqrt{3} $$

Sammanlagt får vi då $\displaystyle{ (\frac{8}{3} + 2\sqrt{3})-(\frac{8}{3} - 2\sqrt{3}) = 4\sqrt{3} }$.
Svaret på uppgiften är alltså $\displaystyle{ 4.\sqrt{3} }$ a.e.

Övning 2.1:5

Beräkna integralerna

a) $\displaystyle \int \displaystyle\frac{dx}{\sqrt{x+9}-\sqrt{x}}\quad$ (Ledning: förläng med nämnarens konjugat)
b) $\displaystyle \int \sin^2 x\quad$ (Ledning: skriv om integranden med en trigonometrisk formel)


Facit 

Facit till alla delfrågor

a)     $\displaystyle\frac{2}{27}\left((x+9)\sqrt{x+9}+x\sqrt{x}\right)+C$
b)     $-\displaystyle\frac{\sin2x}{4}+\frac{x}{2}+C$