Processing Math: Done
To print higher-resolution math symbols, click the
Hi-Res Fonts for Printing button on the jsMath control panel.
No jsMath TeX fonts found -- using image fonts instead.
These may be slow and might not print well.
Use the jsMath control panel to get additional information.
jsMath Control PanelHide this Message

jsMath

Lösning 3.4:1

FörberedandeFysik

(Skillnad mellan versioner)
Hoppa till: navigering, sök
Rad 8: Rad 8:
-
21v2=21(2m/s)2+g(0;7m))v2=4(m/s)2+14(m/s)2=
+
<math>\frac{1}{2}v^2=\frac{1}{2}(2m/s)^2+g(0,7m) \Rightarrow v^2 = 4(m/s)^2+14(m/s)^2= </math>
-
=18(m/s)2)v=p18m/s=4;24m/s
+
<math>=18(m/s)^2 \Rightarrow v = \sqrt{18}m/s = 4,24 m/s</math>

Versionen från 14 januari 2010 kl. 12.02

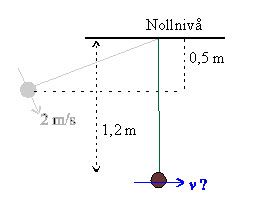
a) Ju längre ner pendeln kommer desto högre är farten. Det betyder att hastigheten är maximal då pendeln är vertikal. Välj upphängningspunkten som nollnivå.

Bild:losning_3_4_1.jpg

Energiprincipen ger att summan av lägesenergi och kinetisk energi är konstant. Energin vid utgångsläget = Energin vid vertikalläget. Antag att partikeln har en massa m.

21m(2ms)2−mg(05m)=21mv2−mg(12m)


21v2=21(2ms)2+g(07m)v2=4(ms)2+14(ms)2=

=18(ms)2v=18ms=424ms 

Den här artikeln är hämtad från http://wiki.math.se/wikis/forberedandefysik/index.php/L%C3%B6sning_3.4:1