Processing Math: Done
To print higher-resolution math symbols, click the
Hi-Res Fonts for Printing button on the jsMath control panel.
No jsMath TeX fonts found -- using image fonts instead.
These may be slow and might not print well.
Use the jsMath control panel to get additional information.
jsMath Control PanelHide this Message

jsMath

Lösning 4.5:2

FörberedandeFysik

(Skillnad mellan versioner)
Hoppa till: navigering, sök
Rad 2: Rad 2:
Bredden på filmen förhåller sig till bredden på byggnaden som sträckorna <math>b</math> till <math>a</math>. <math>a+b=100 m \Rightarrow b\approx 100 m \Rightarrow f=0,045 m</math>.<br\>
Bredden på filmen förhåller sig till bredden på byggnaden som sträckorna <math>b</math> till <math>a</math>. <math>a+b=100 m \Rightarrow b\approx 100 m \Rightarrow f=0,045 m</math>.<br\>
Samma uträkning med höjden på byggnaden medför att <math>f = 0,048 m</math>, men med den brännvidden går inte bredden på byggnaden in på filmen.<br\>
Samma uträkning med höjden på byggnaden medför att <math>f = 0,048 m</math>, men med den brännvidden går inte bredden på byggnaden in på filmen.<br\>
 +
 +
 +
[[Bild:losning_4_5_2.jpg]]

Versionen från 26 januari 2010 kl. 13.37

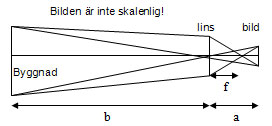
Linsformeln 1a+1b=1f där f är brännvidden (fokalavstånd). Likformiga trianglar ger b80=a0036 a=003680b.
Bredden på filmen förhåller sig till bredden på byggnaden som sträckorna b till a. a+b=100mb100mf=0045m.
Samma uträkning med höjden på byggnaden medför att f=0048m, men med den brännvidden går inte bredden på byggnaden in på filmen.


Bild:losning_4_5_2.jpg

Den här artikeln är hämtad från http://wiki.math.se/wikis/forberedandefysik/index.php/L%C3%B6sning_4.5:2