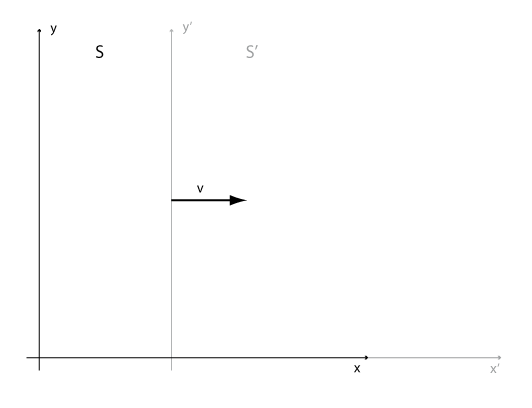5.1 Relativitet
FörberedandeFysik
| Rad 127: | Rad 127: | ||
z′=z | z′=z | ||
| - | <math>t′=\gamma \left(t−\frac{vx}{c^2} \right)</math> | + | <math>t′=\gamma \left(t− \frac{vx}{c^2} \right)</math> |
Där <math>\gamma</math> är Lorentzfaktorn eller gammafaktorn: | Där <math>\gamma</math> är Lorentzfaktorn eller gammafaktorn: | ||
| Rad 142: | Rad 142: | ||
Anta att Emma som befinner sig på tåget mäter längden på tåget till L0. Denna längd kallar vi vilolängden, eftersom tåget befinner sig i vila i förhållande till sig själv (inertialsystemet S′). Per som står på banvallen i systemet S upplever dock att S′ rör sig med farten v och tycker istället att tågets längd är | Anta att Emma som befinner sig på tåget mäter längden på tåget till L0. Denna längd kallar vi vilolängden, eftersom tåget befinner sig i vila i förhållande till sig själv (inertialsystemet S′). Per som står på banvallen i systemet S upplever dock att S′ rör sig med farten v och tycker istället att tågets längd är | ||
| - | <math>L = \frac{L_0}{\gamma} = L_0\,\sqrt{1-frac{v^2}{c^2}}</math>. | + | <math>L = \frac{L_0}{\gamma} = L_0\,\sqrt{1- \frac{v^2}{c^2}}</math>. |
| Rad 172: | Rad 172: | ||
Detta sätts in i sambandet | Detta sätts in i sambandet | ||
| - | <math>\frac{1}{4}c^2 \Delta t^2 = \frac{1}{4} v^2 \Delta t^2 + \frac{1}{4}(c \, \Delta t_0)^2 </math> | + | <math>\frac{1}{4}c^2 \Delta t^2 = \frac{1}{4}\, v^2 \Delta t^2 + \frac{1}{4}\, \left(c \, \Delta t_0 \right)^2 </math> |
Löser vi ut <math>\Delta t</math> får vi formeln för tidsdilatation | Löser vi ut <math>\Delta t</math> får vi formeln för tidsdilatation | ||
Versionen från 21 november 2017 kl. 16.24
| Teori | Övningar |
Mål och innehåll
Innehåll
- Inledning
- Einsteins två postulat
- Michelson-Morleys experiment
- Samtidighet
- Lorentztransformationen
- Längdkontraktion
- Tidsdilatation
- Relativistisk Dopplereffekt
- Hubbles observationer
Läromål
Efter detta avsnitt ska du ha lärt dig att:
- Förklara vad Einsteins postulat leder till
- Redogöra för eterbegreppet och ljusets hastighet i vakuum
- Skilja mellan Galileitransformation och Lorentztransformation
- Räkna på längdkontraktion och tidsdilatation
- Räkna på relativistisk Dopplereffekt
FÖRFATTARE: Göran Tranströmer och Lars-Erik Berg
Teori
Inledning
Innan Albert Einstein presenterade det som kom att kallas relativitetsteorin ansågs den Newtonska mekaniken fullt tillräcklig för att beskriva tid och rum. Det här avsnittet kommer ge en liten introduktion till den så kallade speciella relativitetsteorin som tvingar oss att ifrågasätta vår vardagliga kunskap om begrepp som längd, tid och massa. Idag är teorin experimentellt bevisad och är dessutom viktig för många tekniska tillämpningar. Bland annat används relativitetsteori för att göra korrekta beräkningar inom GPS-tekniken. Innan du börjar läsa detta avsnitt är det bra om du läser avsnittet Koordinatsystem och inertialsystem. Användbara konstanter och enheter finns listade i avsnittet Konstanter och enheter.
Einsteins två postulat
Den speciella relativitetsteorin bygger på Einsteins två postulat:
- Alla naturlagar är desamma för observatörer som rör sig med konstant hastighet i förhållande till varandra.
- Ljuset rör sig med samma hastighet (c=299792458 m/s) i förhållande till alla observatörer oberoende av vilket inertialsystem de befinner sig i.
Det första postulatet innebär att det är omöjligt att bevisa att något inertialsystem verkligen är i rörelse eller verkligen i vila. Det finns alltså inget absolut vilosystem från vilket vi kan mäta all annan rörelse. Ingen rörelse är absolut, all rörelse är relativ. Men det kan vara bra att komma ihåg att då man räknar med relativitetsteorin så tänker man sig alltid att det system man observerar ifrån befinner sig i vila. Man ser det alltså alltid som att det andra systemet rör sig.
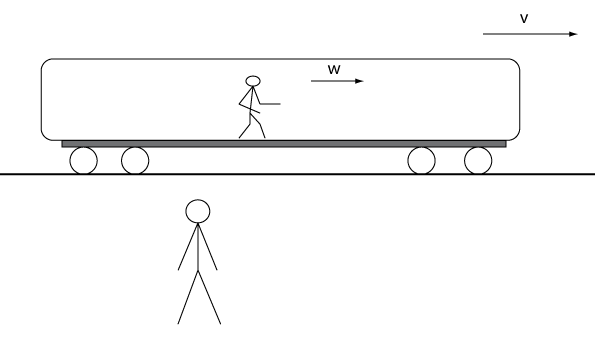
Låt oss fundera på ett exempel med en tågvagn i konstant rörelse. Anta att tåget (inertialsystemet S′) rör sig med hastigheten v i förhållande till Per som står utanför tåget och tycker att han står stilla i sitt system S och ser tåget åka förbi. Säg då att Emma, som befinner sig på tåget, börjar gå genom tåget med konstant hastighet w i tågets färdriktning (se bild nedan). Vilken hastighet tycker då Per att Emma rör sig med? Visst borde väl Per tycka att Emma rör sig med hastigheten u=w+v?
/illustration/
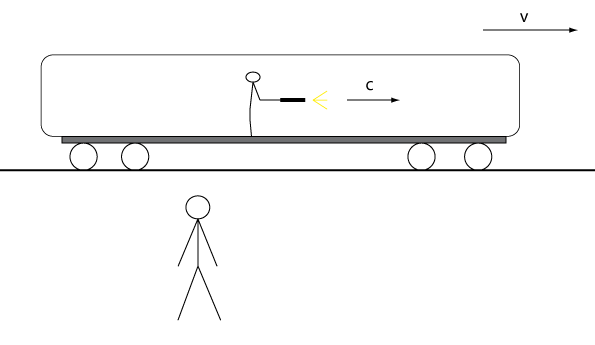
Men säg att Emma inte går genom tåget utan istället lyser med en ficklampa i tågets färdriktning (se bild nedan). Om vi gör som nyss och adderar hastigheten från tåget och hastigheten på ljuset från ficklampan så borde ju Per mäta hastigheten på ljuset till u=c+v. Alltså en högre hastighet än c! Det stämmer ju inte med andra postulatet.
/illustration/
Einstein visade att de två postulaten faktiskt inte är motsägelser, det är bara additionsformeln för hastigheter (u=w+v) som inte stämmer! Om man istället håller fast vid båda postulaten kan man härleda den så kallade Lorentztransformationen. Men kom dock ihåg att i de flesta fall kan vi ändå använda den vanliga additionsformeln för hastigheter. Det är bara då vi räknar med hastigheter nära ljusets hastighet som vi märker någon skillnad. En bra tumregel är att hastigheter som är högre än 0,1c ska behandlas relativistiskt.
Michelson-Morleys experiment
Varför ska man då hålla fast vid det andra postulatet? Ett av de mest kända experimenten som har visat att ljusets hastighet alltid är konstant är Michelson-Morleys experiment som utfördes under senare delen av 1800-talet. Det gick ut på att med hjälp av fysikens lagar mäta jordens hastighet relativt den så kallade etern. Vid denna tid ansåg man att ljus inte kunde utbreda sig i tomma rymden. Man menade att det krävdes ett medium för detta på samma sätt som ljud kräver till exempel luft att utbreda sig i. Denna substans som man hoppades finna i experimentet kallade man för eter efter Aristoteles femte element. Man tänkte sig att denna eter fyllde hela universum.
Jorden rör sig i sin bana runt solen med en hastighet på cirka 30 km/s. Med hjälp av en speciell försöksanordning, en Michelsoninterferometer, jämförde man nu ljusets hastighet, mätt dels parallellt med och dels vinkelrätt mot jordens rörelseriktning runt solen. Försöket upprepades i olika punkter på jordbanan. Eftersom jorden inte kunde vara i vila relativt etern i alla dessa punkter, så borde man vid åtminstone några mättillfällen fått olika värden på ljushastigheten i de två mätriktningarna. Någon sådan skillnad kunde dock inte observeras. Inte nog med att eterhypotesen motbevisades, resultaten av detta försök tydde dessutom på att ljusets hastighet var densamma i alla riktningar, oberoende av observatörens eget rörelsetillstånd. Efter detta experiment har liknande mer förfinade försök utförts som alla säger samma sak: Ljusets hastighet i vakuum är alltid densamma, oberoende av hur ljuskällan eller observatören rör sig!
Samtidighet
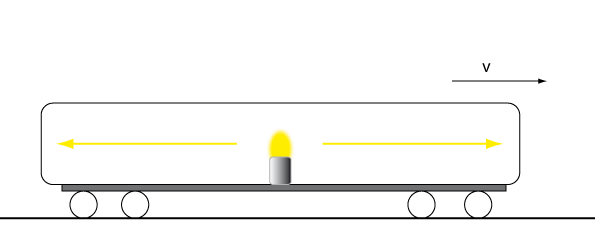
Utgår man från relativitetsteorin blir även begreppet samtidighet relativt. Betrakta återigen exemplet med tåget som rör sig med konstant hastighet i förhållande till banvallen. Anta att vi ställer en blinkande lampa mitt i vagnen (se figur nedan). Emma som befinner sig i vagnen tycker förstås att ljuset kommer träffa vagnens ändar samtidigt eftersom ljuset har lika långt att färdas till båda sidorna. Men Per som står utanför vagnen tycker att ljuset träffar den bakre änden av vagnen först och den främre änden senare. Men även Per tycker att ljuset rör sig lika fort i båda riktningarna, det är bara det att tåget hinner flytta sig under tiden som ljuset utbreder sig, så att ljuset når bakre änden innan det når den främre. Samtidighet är alltså ett relativt begrepp!
/illustration/
Lorentztransformationen
Vi har koordinatsystemen S och S′, där S′ rör sig med den konstanta hastigheten v åt höger relativt S som bilden nedan illustrerar. Vi antar att rörelsen sker rätlinjigt längs x- respektive x′-axeln. Anta också att t=0 då koordinatsystemens origon sammanfaller.
/illustration/
Intuitivt verkar det kanske som att vi kan relatera koordinaterna i de olika systemen till varandra såhär:
x′=x−vt
y′=y
z′=z
t′=t
Denna koordinattransformation kallas för Galileitransformationen. Men på samma sätt som det intuitiva sättet att addera hastigheter är felaktigt så är Galileitransformationen felaktig. Einstein (tillsammans med Lorentz) kom istället fram till den så kallade Lorentztransformationen:
\displaystyle x′=\gamma(x−vt)
y′=y
z′=z
\displaystyle t′=\gamma \left(t− \frac{vx}{c^2} \right)
Där \displaystyle \gamma är Lorentzfaktorn eller gammafaktorn:
\displaystyle \gamma = \frac{1}{ \sqrt{1-v^2/c^2} }
Eftersom v aldrig kan vara större än ljushastigheten c så gäller alltid att γ≥1. För låga hastigheter är dock γ≈1, vilket gör att Lorentztransformationen sammanfaller med Galileitransformationen. Eftersom alla vardagliga hastigheter är relativt låga kan vi i vanliga fall använda vårt intuitiva sätt att transformera koordinater och addera hastigheter med mycket god noggrannhet.
Längdkontraktion
Anta att Emma som befinner sig på tåget mäter längden på tåget till L0. Denna längd kallar vi vilolängden, eftersom tåget befinner sig i vila i förhållande till sig själv (inertialsystemet S′). Per som står på banvallen i systemet S upplever dock att S′ rör sig med farten v och tycker istället att tågets längd är
\displaystyle L = \frac{L_0}{\gamma} = L_0\,\sqrt{1- \frac{v^2}{c^2}}.
Per mäter alltså upp en kortare längd på tåget än vad Emma gör. Notera att det inte är fråga om någon slags optisk synvilla, tåget är faktiskt kortare i S! Längdkontraktion sker dock bara för längder som är parallella med rörelseriktningen. Tågets höjd är alltså både Emma och Per överens om.
Tidsdilatation
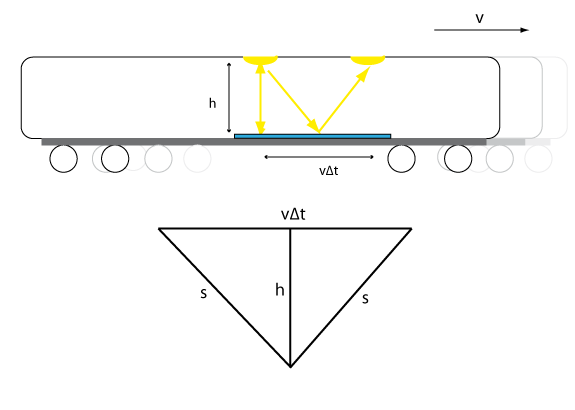
Vad händer nu om vi jämför klockor i systemet S och S′? För att kunna mäta tiden på ett rättvist sätt skulle vi kunna använda oss av ljus, eftersom det färdas med samma hastighet sett från båda systemens perspektiv. Vi skulle till exempel kunna tänka oss att vi har en lampa i tågets tak som är riktad mot golvet där det ligger en spegel. Lampan befinner sig på höjden h över spegeln. Då lampan tänds tycker Emma förstås att ljuset från lampan går rakt ner mot golvet och tillbaka igen eftersom hon befinner sig i tågets vilosystem. Ljuset färdas alltså sträckan 2h med hastigheten c. Det innebär att tiden för hela reflektionen är Δt0=2h/c. Per som tycker att tåget rör sig med farten v kommer tycka att strålen träffar spegeln lite längre mot tågets färdriktning för att åter träffa lampan ytterligare längre åt tågets färdriktning. Detta illustreras i bilden nedan.
/illustration/
Ljusets hastighet är förstås fortfarande c så tiden det tar för ljuset att reflekteras tillbaka till lampan kommer därför att vara längre sett från S eftersom sträckan ljuset färdas nu är 2s istället. Per tycker alltså att tiden det tar för ljuset att reflekteras är Δt=2s/c.
Från triangeln fås sambandet
\displaystyle s^2 = \left(\frac{1}{2}v\Delta t\right)^2 + h^2
Vi har att
\displaystyle \Delta t_0 = 2h/c \Rightarrow h = \frac{1}{2} c\,\Delta t_0
\displaystyle \Delta t = 2 s/c \Rightarrow h = \frac{1}{2} \sqrt{c^2-v^2}\,\Delta t
Detta sätts in i sambandet
\displaystyle \frac{1}{4}c^2 \Delta t^2 = \frac{1}{4}\, v^2 \Delta t^2 + \frac{1}{4}\, \left(c \, \Delta t_0 \right)^2
Löser vi ut \displaystyle \Delta t får vi formeln för tidsdilatation
\displaystyle \Delta t = \frac{\Delta t_0}{\sqrt{1-v^2/c^2}} = \gamma \Delta t_0.
Man har mätt tidsdilatationen genom att jämföra en atomklocka som är kvar på jorden med en som åker runt jorden i ett flygplan. Mätresultaten stämmer helt överens med vad relativitetsteorin förutsäger.
Relativistisk Dopplereffekt
Om en källa som passerar en observatör skickar ut en signal med en viss frekvens så kommer den uppmätta frekvensen hos observatören att ändras, detta fenomen kallas Dopplereffekten. Ett vardagligt exempel är en passerande polisbil med påslagen siren. När polisbilen närmar sig höjs frekvensen vilket gör att sirenen låter ljusare och tvärtom när den passerat och rör sig bortåt. Mer läsning om Dopplereffekten finns på Wikipedia.
Ett annat exempel på Dopplereffekten är de frekvensförändringar som är orsakade av stjärnornas rörelse relativt jorden. Denna effekt gör det möjligt för astronomer att mäta deras hastighet relativt jorden. Dopplereffekten kallas ofta i det här fallet för rödförskjutningen och syftar på att stjärnor och galaxer avlägsnar sig från oss med hög hastighet v. Detta orsakar en frekvensminskning i det ljus vi mottar här på jorden och lägre frekvens innebär ju rödare ljus, därav namnet rödförskjutning. Då fenomenet involverar mycket höga hastigheter krävs relativistiska beräkningar! Den frekvensförändring som Dopplereffekten ger upphov till beskrivs då av formeln:
\displaystyle f = f_0 \sqrt{\frac{1-v/c}{1+v/c}}
där \displaystyle f är den frekvens som uppfattas av observatören, \displaystyle f_0 frekvensen hos sändaren och \displaystyle v hastigheten med vilken sändaren rör sig.
Hubbles observationer
Astronomen Edwin Hubble visade i slutet på 1920-talet att det var Dopplereffekten som var orsaken till att avlägsna stjärnor avgav rödare ljus.
På så sätt drogs också slutsatsen att stjärnorna rör sig bort från oss. Denna slutsats har lett till teorier om universums expansion och att tätheten av materia därför minskar med tiden. Det är då naturligt att räkna bakåt i tiden. Går man 13,7 miljarder år tillbaka når man ett startillstånd med mycket hög materiatäthet och temperatur som kallas Big Bang.
Råd för inläsning
Tänk på att...
En sådan enkel hypotes som att ljusets hastighet är konstant och den maximala hastigheten i vakuum leder till Lorentztransformationen - som förklarar tidsdilatation, relativistisk massa, relativistisk dopplereffekt etc.
Lästips
För dig som behöver en längre förklaring eller vill fördjupa dig ytterligare, vill vi tipsa om:
HEUREKA! Fysik 1, kapitel 12, Relativitet: sidorna 281-290, samt
Halliday and Resnick, Fundamentals of Physics, Wiley Benson, University physics, Wiley
Läs mer om | relativitetsteorin på svenska Wikipedia.
Länktips
Läs, lyssna och titta på multimedia om Einsteins relativitetsteori från NOVA "Einstein's Big Idea"
(c) Copyright 2017, KTH Matematik