5.4 Atomen
FörberedandeFysik
| (16 mellanliggande versioner visas inte.) | |||
| Rad 41: | Rad 41: | ||
:''Balmerserien hos atomärt väte.'' | :''Balmerserien hos atomärt väte.'' | ||
| - | =Bohrs teori för väteatomen= | + | ==Bohrs teori för väteatomen== |
Uppmuntrad av Plancks framgång med kvantisering kom Bohrs teori för väteatomen (1913). Den innebar att i ett bundet (atomärt) system är energin kvantiserad. Systemets möjliga energitillstånd kan åskådliggöras med ett energinivådiagram, där (i den enklaste modellen) varje nivå tilldelas ''ett'' kvanttal <math>n</math>. Genom absorption av elektromagnetisk strålning eller genom kollisioner med omgivande atomer överförs kinetisk energi till elektronen, som exciteras; den motsatta deexcitationsprocessen sker under fotonemission. | Uppmuntrad av Plancks framgång med kvantisering kom Bohrs teori för väteatomen (1913). Den innebar att i ett bundet (atomärt) system är energin kvantiserad. Systemets möjliga energitillstånd kan åskådliggöras med ett energinivådiagram, där (i den enklaste modellen) varje nivå tilldelas ''ett'' kvanttal <math>n</math>. Genom absorption av elektromagnetisk strålning eller genom kollisioner med omgivande atomer överförs kinetisk energi till elektronen, som exciteras; den motsatta deexcitationsprocessen sker under fotonemission. | ||
| Rad 54: | Rad 54: | ||
På samma sätt betecknar <math>\gamma</math> ett hopp som hoppar över två skal, och så vidare. | På samma sätt betecknar <math>\gamma</math> ett hopp som hoppar över två skal, och så vidare. | ||
| - | =Bohrs tre postulat= | + | ==Bohrs tre postulat== |
# Elektronen kretsar i stabila banor utan att stråla ut energi. | # Elektronen kretsar i stabila banor utan att stråla ut energi. | ||
| Rad 115: | Rad 115: | ||
av <math>n</math> | av <math>n</math> | ||
| - | <math>E_n = - \displaystyle\frac{e^2}{8 \pi \epsilon_0} \cdot \frac{m e^2 \pi}{n^2 \epsilon_0 | + | <math>E_n = - \displaystyle\frac{e^2}{8 \pi \epsilon_0} \cdot \frac{m e^2 \pi}{n^2 \epsilon_0 h^2}</math> |
| - | h^2} | + | |
| - | = - \displaystyle\frac{m e^4}{8 h^2 \epsilon_0^2} \cdot \displaystyle\frac{1}{n^2} | + | <math>= - \displaystyle\frac{m e^4}{8 h^2 \epsilon_0^2} \cdot \displaystyle\frac{1}{n^2}</math> |
| - | = E_0 \cdot \frac{1}{n^2}</math> | + | <math>= E_0 \cdot \frac{1}{n^2}</math> |
där <math>E_0</math> är vätets joniseringsenergi, den energi som måste tillföras för att en atom i viloläge ska frigöra en elektron helt. Med numeriska värden för <math>m</math>, <math>e</math>, <math>h</math> och <math>\epsilon_0</math> får vi <math>E_0 = -13{,}61 \,\mbox{eV}</math>. | där <math>E_0</math> är vätets joniseringsenergi, den energi som måste tillföras för att en atom i viloläge ska frigöra en elektron helt. Med numeriska värden för <math>m</math>, <math>e</math>, <math>h</math> och <math>\epsilon_0</math> får vi <math>E_0 = -13{,}61 \,\mbox{eV}</math>. | ||
| Rad 127: | Rad 126: | ||
<math>E_n = E_0\cdot \displaystyle \frac{1}{n^2} = -13{,}61\cdot \displaystyle\frac{1}{n^2} \,\mbox{eV}</math> | <math>E_n = E_0\cdot \displaystyle \frac{1}{n^2} = -13{,}61\cdot \displaystyle\frac{1}{n^2} \,\mbox{eV}</math> | ||
| - | |||
där <math>n</math> är huvudkvanttalet och kan anta värdena <math>1,2,3,\dots</math> | där <math>n</math> är huvudkvanttalet och kan anta värdena <math>1,2,3,\dots</math> | ||
| - | '' | + | ==Energinivåer hos väteatomen== |
| + | |||
| + | Materia består av atomer, varje atom består av en mycket liten men tung kärna och ett elektronmoln. Varje elektron har noggrant bestämd energi. Varje atom har många olika energinivåer. Varje atom som är exciterad gör sig av med överskottsenergin. Då övergår en elektron från en bana med högre energi till en med lägre och atomen sänder ut energin som en foton. | ||
| + | Energidifferensen mellan två nivåer <math>E_n</math> och <math>E_k</math> fås som | ||
| + | |||
| + | <math>E_n – E_k | ||
| + | = -\displaystyle\frac{me^4}{8\epsilon_0^2h^2} \cdot \displaystyle \frac{1}{n^2} | ||
| + | - \bigg(-\displaystyle\frac{me^4}{8\epsilon_0^2h^2}\bigg) \cdot \displaystyle \frac{1}{k^2} | ||
| + | = -\displaystyle\frac{me^4}{8\epsilon_0^2h^2} \cdot | ||
| + | \bigg( \displaystyle \frac{1}{n^2}- \displaystyle \frac{1}{k^2} \bigg)</math> | ||
| + | <math> | ||
| + | = E_0 \cdot \bigg( \displaystyle \frac{1}{n^2}-\displaystyle \frac{1}{k^2} \bigg) | ||
| + | = -13{,}61 \mbox{ eV} \cdot \bigg( \displaystyle \frac{1}{n^2}-\displaystyle \frac{1}{k^2} \bigg) | ||
| + | </math> | ||
| + | |||
| + | Från Plancks lag känner vi att vi också kan skriva energidifferensen som | ||
| + | |||
| + | <math>E_n - E_k = hf = \displaystyle \frac{hc}{\lambda}</math> | ||
| + | |||
| + | Sätter vi samman dessa båda uttryck har vi | ||
| + | |||
| + | <math>\displaystyle \frac{hc}{\lambda} | ||
| + | = E_0 \cdot \bigg( \displaystyle \frac{1}{n^2}-\displaystyle \frac{1}{k^2} \bigg)</math> | ||
| + | |||
| + | varur vi får | ||
| + | |||
| + | <math>\displaystyle\frac{1}{\lambda} | ||
| + | = \displaystyle\frac{E_0}{hc} | ||
| + | \cdot \bigg( \displaystyle \frac{1}{n^2}-\displaystyle \frac{1}{k^2} \bigg)</math> | ||
| + | |||
| + | konstanten <math>\displaystyle\frac{E_0}{hc}</math> är så pass vanlig att den fått ett eget namn, Rydbergs konstant, <math>R</math> | ||
| + | |||
| + | <math>R = 1,097 \cdot 10^7 \mbox{m}^{-1}</math> | ||
| + | |||
| + | Våglängden på den foton som sänds ut vid en energiövergång fås alltså av sambandet | ||
| + | |||
| + | <math>\displaystyle\frac{1}{\lambda} | ||
| + | = R | ||
| + | \cdot \bigg( \displaystyle \frac{1}{n^2}-\displaystyle \frac{1}{k^2} \bigg) </math> | ||
| + | |||
| + | [[Bild:5.4_energinivådiagram.jpg]] | ||
| + | : Energinivådiagram hos väteatomen. | ||
| + | |||
| + | För Balmerserien, som utgår från lager <math>2</math>, har vi (jämför med inledande samband) | ||
| + | |||
| + | <math>\displaystyle\frac{1}{\lambda} | ||
| + | = R \bigg( \displaystyle\frac{1}{2^2} - \displaystyle\frac{1}{k^2} \bigg)</math> | ||
| + | |||
| + | <math>\Rightarrow \lambda | ||
| + | = \displaystyle \frac{1}{R \bigg( \displaystyle\frac{1}{2^2} - \displaystyle\frac{1}{k^2} \bigg)} | ||
| + | =\displaystyle\frac{2^2}{R} \cdot \displaystyle\frac{k^2}{k^2-2^2} | ||
| + | = 364,5 \cdot \displaystyle\frac{k^2}{k^2-2^2} \mbox{nm}</math> | ||
| + | |||
| + | ==Större atomer== | ||
| + | |||
| + | Genom att ta hänsyn till atomens storlek kan man få många av sambanden för | ||
| + | väte att gälla även större atomer. Vi finner att för en större atom med atomnummer <math>Z</math> gäller | ||
| + | |||
| + | |||
| + | Banradien <math>r</math> i bana <math>n</math> ges av | ||
| + | |||
| + | <math>r_n = a_0 \cdot \displaystyle\frac{n^2}{Z^2}</math> | ||
| + | |||
| + | med Bohrradien <math>a_0= 0{,}0529 \,\mbox{nm}</math> | ||
| + | |||
| + | Banhastighet <math>v</math> i bana <math>n</math> ges av | ||
| + | |||
| + | <math>v_n = \displaystyle\frac{Z e^2}{2 \epsilon_0 h n}</math> | ||
| + | |||
| + | Balmers formel utökad till större atomer | ||
| + | |||
| + | <math>\displaystyle\frac{1}{\lambda} | ||
| + | = R Z^2 \bigg( \displaystyle\frac{1}{n^2} - \displaystyle\frac{1}{k^2} \bigg)</math> | ||
| + | |||
| + | ---- | ||
| + | |||
| + | =Laser= | ||
| + | |||
| + | ==Hur fungerar en laser?== | ||
| + | |||
| + | [[Bild:5.4_laser.jpg]] | ||
| + | |||
| + | Om man tillför det instängda mediet energi i form av en ljusblixt eller elektricitet då kommer ljuset att självsvänga mellan speglarna så att när ljuset går fram och tillbaka kommer alla ljusstrålar att svänga i takt med varandra. På så sätt kommer allt ljus att ha samma våglängd (färg). | ||
| + | |||
| + | ==Ljusförstärkning genom stimulerad ljusemission== | ||
| + | |||
| + | Exciterade atomer sänder vanligtvis ut oordnat ljus (spontan emission), dvs dels slumpmässigt i tiden, dels slumpmässigt i riktning. Men en exciterad atom kan fås att sända ut välordnat ljus vid stimulerad emission. En förutsättning för att stimulerad emission ska inträffa är att det finns fler atomer i det exiterade tillståndet än i grundtillståndet. Detta kallas populationsinversion. När man har blinkat med blixtlampan en gång, vilket kallas pumpning, exciteras en viss mängd atomer. Dessa atomer kommer att sända ut var sin foton. Om en foton med samma energi som atomens överskottsenergi passerar atomen, så sänder den ut sitt ljuskvantum just då, i takt med den passerande fotonen, i samma riktning. Det blir då två likadana fotoner på en gång. Om det finns många exciterade atomer så kan en foton starta en ström av fotoner, i samma riktning och i takt. Det kallas koherent ljus (sammanhängande). | ||
| + | |||
| + | [[Bild:5.4_ljusemission.jpg]] | ||
| + | |||
| + | Den första lasern var en rubidiumlaser som syns nedan. | ||
| + | |||
| + | [[Bild:5.4_rubidium.jpg]] | ||
| + | |||
| + | ---- | ||
| + | |||
| + | =Nanofysik= | ||
| + | |||
| + | Nanofysik och nanoteknik är ett av de mest spännande teknik- och forskningsområdena idag. | ||
| + | Ordet nano kommer från grekiska och betyder dvärg eller liten. När nano används som prefix betyder det en miljarddel. Inom nanoteknik är det saker som är mellan <math>1</math> och <math>100</math> nanometer, förkortat <math>\mathrm{nm}</math>, som man talar om. Atomer är mindre än en <math>\mathrm{nm}</math>, molekyler och celler varierar i storlek från <math>1</math> till flera <math>\mathrm{nm}</math>. Nano betyder miljarddel, och en nanometer <math>\mathrm{nm}</math> är så litet att det inte kan ses i ett vanligt ljusmikroskop. Nanovetenskap och nanoteknik handlar om att studera och skräddarsy materialstrukturer i storleksordningen <math>1-\, 100\,\mathrm{ nm}</math> (som jämförelse är en atom cirka <math>0,2\,\mathrm{ nm}</math> stor). | ||
| + | |||
| + | Forskarna arbetar alltså med materia på atomnivå och skapar material och komponenter med helt nya egenskaper – för användning inom bland annat mikroelektronik och biomedicin. | ||
| + | |||
| + | Nanoteknik är egentligen ett samlingsnamn för olika vetenskapliga nanoområden och tvärvetenskapliga samarbeten är ofta en förutsättning för att kunna lösa nanorelaterade problemställningar. | ||
| + | |||
| + | [[Bild:5.4_corrals.jpg]] | ||
| + | |||
| + | Nanotekniken är en naturlig utveckling inom flera teknikområden. Inom elektroniken har man gjort transistorerna mindre för att de ska bli snabbare och få plats fler, så att t ex en hemdator blir bättre. De instrument och maskiner som man tagit fram för mikroelektroniken har gjort det möjligt att studera naturens minsta beståndsdelar, till exempel Gecko-fötter, och gjort det möjligt att skapa material i nanometerstorlek. Molekyler och celler har visserligen alltid varit nanoteknik, men nu finns det möjligheter att koppla ihop biologi och elektronik. | ||
| + | |||
| + | [[Bild:5.4_atomer.jpg]] | ||
| + | |||
| + | Man frågar sig om nanopartiklar kan vara farliga. Det beror på om man talar om saker i nanostorlek eller om en yta som är nanostrukturerad. Om det kan avges stora mängder med små partiklar är det givetvis farligt, eftersom det kan skada lungorna om man inandas partiklarna. Men nanometerstora partiklar finns redan omkring oss, till exempel i avgaser och trafikdamm och tonerpulvret i en kopiator eller laserskrivare. En glasyta som är nanostrukturerad för att hålla sig ren avger dock inga partiklar. | ||
| + | |||
| + | ==Röntgendiffraktion== | ||
| + | |||
| + | Materialfysiken söker ett samband mellan ett materials makroskopiska egenskaper och dess mikroskopiska, atomära och elektroniska struktur för att kunna förstå, modellera och modifiera sammansättning och egenskaper. Man frågar sig dels vilka slags atomer (kemisk identifiering) som förekommer i strukturen och dels hur de sitter geometriskt. I de flesta fasta material är atomerna arrangerade, åtminstone lokalt, i välordnade kristallstrukturer. För att bestämma kristallstrukturen används olika former av diffraktionsbaserade tekniker. Den vanligaste och mest kraftfulla formen är röntgendiffraktion (XRD). För att studera kristallstrukturer med atomavstånd på ett fåtal Ångström måste man använda våglängder i samma storleksordning. En vanlig röntgenkälla är <math>\mathrm{Cu\, K_{\alpha}}</math> med våglängden 1.54 Å. Röntgendiffraktion i kristaller kan betraktas som interferens mellan reflexer från närliggande plan i samma planskara, enligt figuren. Den infallande strålen beskrivs av vågvektorn <math>\mathbf k</math>, och den reflekterade strålen av vågvektorn <math>\mathbf{k'}</math>. Ändringen i vågvektor <math>\Delta\,\mathbf{ k = k -\, k'}</math>. För att interferensen ska vara konstruktiv gäller Braggs lag <math>2d\sin \theta = m\lambda</math> som beskrivs i 5.3. | ||
| + | |||
| + | ==Elektronmikroskopi== | ||
| + | |||
| + | Elektronmikroskopet är ett mångsidigt instrument som används för att erhålla strukturell, magnetisk och elektronisk information om ett prov. Med olika avbildningstekniker, elektrondiffraktion och spektroskopi kan dessa materialegenskaper bestämmas med en rumsupplösning ner till <math>\mathrm{1Å}</math>. Fokuserad elektron- eller jonstråle används för att analysera eller strukturera material på nanometernivå. | ||
| + | |||
| + | Elektronmikroskopi bidrar i sökandet efter unika material både inom tillämpad och grundläggande forskning genom analys på atomär nivå. Med denna kunskap kan ett materials meso- och makroskopiska egenskaper samt samband mellan struktur och mekaniska egenskaper karaktäriseras. Elektronmikroskopi lämpar sig väl för att studera strukturella förändringar och egenskaper hos polymerer, metaller, keramer och biologiska material. Nanokristallina material med kornstorlekar mellan en till tio nm uppvisar helt nya magnetiska, elektriska och optiska egenskaper. Högupplösande elektronmikroskopi är en kraftfull teknik för att studera kristallorientering, fas samt kemisk sammansätting hos ett elektrontransparent tunt prov. Elektronstrålens växelverkan med ett magnetiskt prov används för att studera och visualisera domänmönster samt magnetisering hos magnetiska endomänpartiklar. För detta används elektronholografi och magnetisk avbildning med Lorentzmikroskopi. | ||
| + | |||
| + | ==Spinntronik== | ||
| + | |||
| + | Spinntronik använder elektronernas spinn för att hantera information. Spinnet är mätbart som magnetism och om man kan ställa in spinnet kan man använda elektronernas magnetiska nord- och sydpoler för att representera ettor och nollor. Det innebär att man kan göra de elektroniska kretsarna mycket mindre än vad som är tänkbart med vanlig elektronik. | ||
| + | |||
| + | ==Kvantbit== | ||
| + | |||
| + | Kvantbit, eller qubit, från en. ''quantum binary digit'', representerar den minsta enheten kvantinformation. Den fundamentala skillnaden mellan en kvantbit och klassisk bit är att den senare kan bara vara ha värdet <math>0</math> eller <math>1</math>.En kvantbit motsvarar ett kvanttillstånd, en linjär superposition, s.k. kvantsuperposition. | ||
| + | |||
| + | <div class="inforuta" style="width: 580px"> | ||
| + | ===Råd för inläsning=== | ||
| + | |||
| + | ====Tänk på att...==== | ||
| + | |||
| + | Begreppet laser ('''L'''ight '''A'''mplification by '''S'''timulated '''E'''mission of '''R'''adiation) har onekligen ett skimmer av science fiction över sig, men är idag en väldigt vanlig teknik som används i vårt dagliga liv. När vi handlar är det en laserstråle som läser av varornas priskoder, och det är laser som läser av informationen på våra cd- och dvd-skivor. På de flesta kontor finns det skrivare och kopiatorer som använder laser, och mycket av informationen som skickas mellan datorer och telefoner skickas via optiska fibrer, som även de fungerar med hjälp av laserljus. | ||
| + | |||
| + | ====Lästips==== | ||
| + | |||
| + | För dig behöver en längre förklaring eller som vill fördjupa dig ytterligare, vill vi tipsa om: | ||
| + | |||
| + | : ''HEUREKA! Fysik 2'', kapitel 14, Atomen: sidorna 267 - 283 | ||
| + | |||
| + | : Halliday and Resnick, ''Fundamentals of physics'', Wiley | ||
| + | |||
| + | : [http://sv.wikipedia.org/wiki/Atom Läs mer om atomen på svenska Wikipedia] | ||
| + | |||
| + | : [http://sv.wikipedia.org/wiki/Laser Läs mer om laser på svenska Wikipedia] | ||
| + | |||
| + | : [https://www.stralsakerhetsmyndigheten.se/lattlast/laser/ Lättläst om laser från SSM] | ||
| + | |||
| + | : [http://fof.se/tidning/2003/7/john-dalton-atomen Läs mer om John Dalton & atomen i "Forskning & Framsteg"] | ||
| + | |||
| + | </div> | ||
Nuvarande version
| Teori | Övningar |
Mål och innehåll
Innehåll:
- Atomen
- Bohrs tre postulat
- Energinivåer
- Laser
- Stimulerad emission
Läromål
Efter detta avsnitt ska du ha lärt dig att:
- Definiera Balmervåglängderna (Rydbergs formel för väte).
- Redogöra för Bohrs tre postulat energinivåernas kvantisering.
- Förklara hur en laser fungerar.
- Ställa upp och beräkna våglängden vid atomövergångar.
FÖRFATTARE: Göran Tranströmer & Lars-Erik Berg, KTH Fysik
Atomen
Spektroskopin gav att varje grundämne har ett karakteristiskt spektrum. För vissa ämnen (väte, vissa alkalimetaller) var spektrallinjerna regelbundna, lätt igenkännliga serier. Balmer fann för de synliga våglängderna i vätets spektrum att
\displaystyle \lambda_n = konst \cdot \displaystyle \frac{n^2}{n^2 - 2^2}
där \displaystyle n är det skal som elektronen exciteras till, \displaystyle n = 3,4,5... Längre fram i teorin visar vi hur vi kommer fram till detta samband.
- Balmerserien hos atomärt väte.
Bohrs teori för väteatomen
Uppmuntrad av Plancks framgång med kvantisering kom Bohrs teori för väteatomen (1913). Den innebar att i ett bundet (atomärt) system är energin kvantiserad. Systemets möjliga energitillstånd kan åskådliggöras med ett energinivådiagram, där (i den enklaste modellen) varje nivå tilldelas ett kvanttal \displaystyle n. Genom absorption av elektromagnetisk strålning eller genom kollisioner med omgivande atomer överförs kinetisk energi till elektronen, som exciteras; den motsatta deexcitationsprocessen sker under fotonemission.
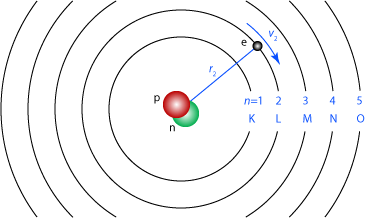
Runt en proton med laddningen \displaystyle \mathrm{e^+} kretsar en elektron med motsatt laddning. Protonens massa är 1836 gånger tyngre än elektronens, så i den enklaste beskrivningen rör sig elektronen i en cirkulär bana runt den stillaliggande (oändligt tunga) protonen.
Banorna kallas skal, och betecknas med bokstäver i alfabetisk ordning inifrån och ut, där det innerska skalet betecknas K. Ett sätt att beteckna hopp mellan skal är att använda det grekiska alfabetet. K\displaystyle _\alpha betecknar ett hopp som hoppar över noll andra skal, så det är detsamma som ett hopp från L-skalet till K-skalet. \displaystyle \beta betecknar hopp som hoppar över ett skal, så K\displaystyle _\beta betecknar ett hopp från M-skalet till K-skalet. L\displaystyle _\beta betecknar ett hopp från N-skalet till L-skalet.
På samma sätt betecknar \displaystyle \gamma ett hopp som hoppar över två skal, och så vidare.
Bohrs tre postulat
- Elektronen kretsar i stabila banor utan att stråla ut energi.
- Då elektronen övergår från en stabil bana till en annan stabil bana absorberar eller emitterar den energin \displaystyle E_i - \,E_f = hf_{if}
- Integralen av elektronens rörelsemängd \displaystyle p runt elektronbanan är en heltalsmultipel av \displaystyle h. \displaystyle \oint p\, ds = n\, h
Eftersom elektronerna rör sig med konstant hastighet i en cirkulär bana \displaystyle s med konstant avstånd \displaystyle r till kärnan kommer rörelsemomentet \displaystyle p i postulat 3 ovan att vara oberoende av banan. Vi får för VL
\displaystyle \oint p ds = p \oint ds = pr \int\limits_0^{2\pi}d\theta = pr\cdot 2\pi
Då \displaystyle p = mv kan vi nu skriva postulat 3 som
\displaystyle mv \cdot 2\pi = nh \iff v =\displaystyle \frac{n h}{2\pi m r}
där \displaystyle n är ett positivt heltal, \displaystyle h Plancks konstant, \displaystyle r avståndet mellan elektronen och kärnan, \displaystyle v elektronens hastighet och \displaystyle m elektronens massa.
En elektron i en omloppsbana kring en atomkärna påverkas av två krafter,
coulombkraften och centipetalkraften. Dessa är lika stora. I \displaystyle r-led har vi alltså
med laddningen \displaystyle q = e följande
\displaystyle \displaystyle\frac{e^2}{4\pi \epsilon_0 r^2} = \displaystyle\frac{m v^2}{r}
där \displaystyle \epsilon_0 är kapacitiviteten i rymden,
\displaystyle \epsilon_0 \approx 8,854 \cdot 10^{-12} \,\mbox{F/m}
Om vi kombinerar de båda senaste sambanden får vi \displaystyle r som en funktion av \displaystyle n enligt
\displaystyle \displaystyle\frac{e^2}{4 \pi\epsilon_0 r^2} = \displaystyle\frac{m}{r} \cdot \bigg(\displaystyle\frac{nh}{2 \pi m r}\bigg)^2 \Rightarrow r_n = \displaystyle\frac{ \epsilon_0 h^2}{m e^2 \pi}\cdot n^2 = a_0\cdot n^2
där \displaystyle a_0 är Bohrradien, \displaystyle a_0= 0{,}0529 \,\mbox{nm}
Elektronens energi, \displaystyle E, utan hänsyn tagen till viloenergin, är summan av
den kinetiska och den potentiella energin.
\displaystyle E = \displaystyle\frac{1}{2} m v^2 - \displaystyle\frac{e^2}{4 \pi \epsilon_0 r}
\displaystyle = \displaystyle\frac{1}{2}m \,v^2 - m \,v^2 = - \frac{1}{2} m\,v^2
\displaystyle = - \displaystyle\frac{e^2}{8 \pi \epsilon_0 r}
Energin är negativ eftersom elektronen är bunden till kärnan.
Om vi sätter in vårt uttryck för \displaystyle r i detta får vi \displaystyle E som en funktion
av \displaystyle n
\displaystyle E_n = - \displaystyle\frac{e^2}{8 \pi \epsilon_0} \cdot \frac{m e^2 \pi}{n^2 \epsilon_0 h^2}
\displaystyle = - \displaystyle\frac{m e^4}{8 h^2 \epsilon_0^2} \cdot \displaystyle\frac{1}{n^2}
\displaystyle = E_0 \cdot \frac{1}{n^2}
där \displaystyle E_0 är vätets joniseringsenergi, den energi som måste tillföras för att en atom i viloläge ska frigöra en elektron helt. Med numeriska värden för \displaystyle m, \displaystyle e, \displaystyle h och \displaystyle \epsilon_0 får vi \displaystyle E_0 = -13{,}61 \,\mbox{eV}.
Vi har alltså för en elektron i omloppsbana energisambandet
\displaystyle E_n = E_0\cdot \displaystyle \frac{1}{n^2} = -13{,}61\cdot \displaystyle\frac{1}{n^2} \,\mbox{eV}
där \displaystyle n är huvudkvanttalet och kan anta värdena \displaystyle 1,2,3,\dots
Energinivåer hos väteatomen
Materia består av atomer, varje atom består av en mycket liten men tung kärna och ett elektronmoln. Varje elektron har noggrant bestämd energi. Varje atom har många olika energinivåer. Varje atom som är exciterad gör sig av med överskottsenergin. Då övergår en elektron från en bana med högre energi till en med lägre och atomen sänder ut energin som en foton. Energidifferensen mellan två nivåer \displaystyle E_n och \displaystyle E_k fås som
\displaystyle E_n – E_k = -\displaystyle\frac{me^4}{8\epsilon_0^2h^2} \cdot \displaystyle \frac{1}{n^2} - \bigg(-\displaystyle\frac{me^4}{8\epsilon_0^2h^2}\bigg) \cdot \displaystyle \frac{1}{k^2} = -\displaystyle\frac{me^4}{8\epsilon_0^2h^2} \cdot \bigg( \displaystyle \frac{1}{n^2}- \displaystyle \frac{1}{k^2} \bigg) \displaystyle = E_0 \cdot \bigg( \displaystyle \frac{1}{n^2}-\displaystyle \frac{1}{k^2} \bigg) = -13{,}61 \mbox{ eV} \cdot \bigg( \displaystyle \frac{1}{n^2}-\displaystyle \frac{1}{k^2} \bigg)
Från Plancks lag känner vi att vi också kan skriva energidifferensen som
\displaystyle E_n - E_k = hf = \displaystyle \frac{hc}{\lambda}
Sätter vi samman dessa båda uttryck har vi
\displaystyle \displaystyle \frac{hc}{\lambda} = E_0 \cdot \bigg( \displaystyle \frac{1}{n^2}-\displaystyle \frac{1}{k^2} \bigg)
varur vi får
\displaystyle \displaystyle\frac{1}{\lambda} = \displaystyle\frac{E_0}{hc} \cdot \bigg( \displaystyle \frac{1}{n^2}-\displaystyle \frac{1}{k^2} \bigg)
konstanten \displaystyle \displaystyle\frac{E_0}{hc} är så pass vanlig att den fått ett eget namn, Rydbergs konstant, \displaystyle R
\displaystyle R = 1,097 \cdot 10^7 \mbox{m}^{-1}
Våglängden på den foton som sänds ut vid en energiövergång fås alltså av sambandet
\displaystyle \displaystyle\frac{1}{\lambda} = R \cdot \bigg( \displaystyle \frac{1}{n^2}-\displaystyle \frac{1}{k^2} \bigg)
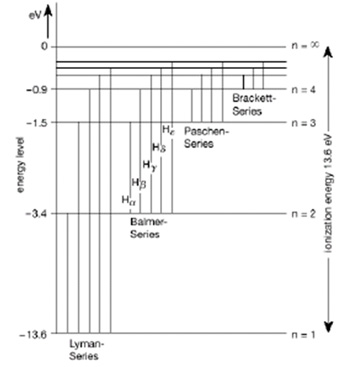
- Energinivådiagram hos väteatomen.
För Balmerserien, som utgår från lager \displaystyle 2, har vi (jämför med inledande samband)
\displaystyle \displaystyle\frac{1}{\lambda} = R \bigg( \displaystyle\frac{1}{2^2} - \displaystyle\frac{1}{k^2} \bigg)
\displaystyle \Rightarrow \lambda = \displaystyle \frac{1}{R \bigg( \displaystyle\frac{1}{2^2} - \displaystyle\frac{1}{k^2} \bigg)} =\displaystyle\frac{2^2}{R} \cdot \displaystyle\frac{k^2}{k^2-2^2} = 364,5 \cdot \displaystyle\frac{k^2}{k^2-2^2} \mbox{nm}
Större atomer
Genom att ta hänsyn till atomens storlek kan man få många av sambanden för väte att gälla även större atomer. Vi finner att för en större atom med atomnummer \displaystyle Z gäller
Banradien \displaystyle r i bana \displaystyle n ges av
\displaystyle r_n = a_0 \cdot \displaystyle\frac{n^2}{Z^2}
med Bohrradien \displaystyle a_0= 0{,}0529 \,\mbox{nm}
Banhastighet \displaystyle v i bana \displaystyle n ges av
\displaystyle v_n = \displaystyle\frac{Z e^2}{2 \epsilon_0 h n}
Balmers formel utökad till större atomer
\displaystyle \displaystyle\frac{1}{\lambda} = R Z^2 \bigg( \displaystyle\frac{1}{n^2} - \displaystyle\frac{1}{k^2} \bigg)
Laser
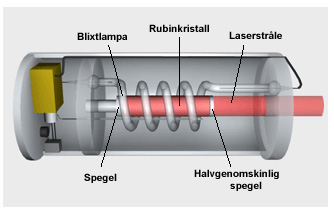
Hur fungerar en laser?
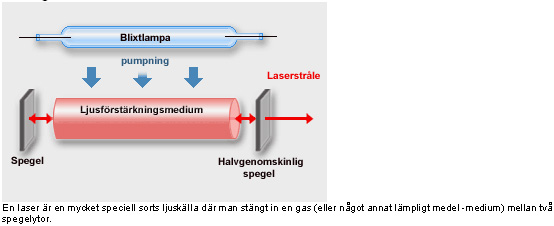
Om man tillför det instängda mediet energi i form av en ljusblixt eller elektricitet då kommer ljuset att självsvänga mellan speglarna så att när ljuset går fram och tillbaka kommer alla ljusstrålar att svänga i takt med varandra. På så sätt kommer allt ljus att ha samma våglängd (färg).
Ljusförstärkning genom stimulerad ljusemission
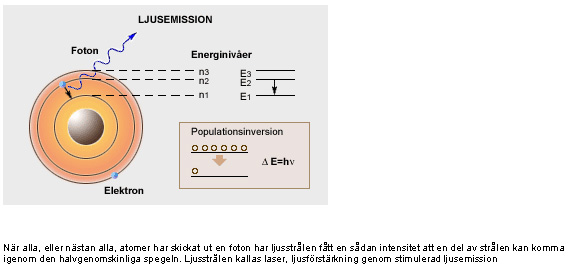
Exciterade atomer sänder vanligtvis ut oordnat ljus (spontan emission), dvs dels slumpmässigt i tiden, dels slumpmässigt i riktning. Men en exciterad atom kan fås att sända ut välordnat ljus vid stimulerad emission. En förutsättning för att stimulerad emission ska inträffa är att det finns fler atomer i det exiterade tillståndet än i grundtillståndet. Detta kallas populationsinversion. När man har blinkat med blixtlampan en gång, vilket kallas pumpning, exciteras en viss mängd atomer. Dessa atomer kommer att sända ut var sin foton. Om en foton med samma energi som atomens överskottsenergi passerar atomen, så sänder den ut sitt ljuskvantum just då, i takt med den passerande fotonen, i samma riktning. Det blir då två likadana fotoner på en gång. Om det finns många exciterade atomer så kan en foton starta en ström av fotoner, i samma riktning och i takt. Det kallas koherent ljus (sammanhängande).
Den första lasern var en rubidiumlaser som syns nedan.
Nanofysik
Nanofysik och nanoteknik är ett av de mest spännande teknik- och forskningsområdena idag. Ordet nano kommer från grekiska och betyder dvärg eller liten. När nano används som prefix betyder det en miljarddel. Inom nanoteknik är det saker som är mellan \displaystyle 1 och \displaystyle 100 nanometer, förkortat \displaystyle \mathrm{nm}, som man talar om. Atomer är mindre än en \displaystyle \mathrm{nm}, molekyler och celler varierar i storlek från \displaystyle 1 till flera \displaystyle \mathrm{nm}. Nano betyder miljarddel, och en nanometer \displaystyle \mathrm{nm} är så litet att det inte kan ses i ett vanligt ljusmikroskop. Nanovetenskap och nanoteknik handlar om att studera och skräddarsy materialstrukturer i storleksordningen \displaystyle 1-\, 100\,\mathrm{ nm} (som jämförelse är en atom cirka \displaystyle 0,2\,\mathrm{ nm} stor).
Forskarna arbetar alltså med materia på atomnivå och skapar material och komponenter med helt nya egenskaper – för användning inom bland annat mikroelektronik och biomedicin.
Nanoteknik är egentligen ett samlingsnamn för olika vetenskapliga nanoområden och tvärvetenskapliga samarbeten är ofta en förutsättning för att kunna lösa nanorelaterade problemställningar.
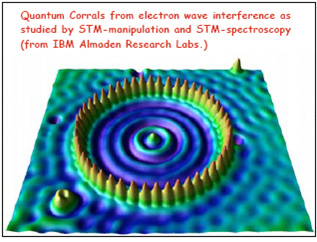
Nanotekniken är en naturlig utveckling inom flera teknikområden. Inom elektroniken har man gjort transistorerna mindre för att de ska bli snabbare och få plats fler, så att t ex en hemdator blir bättre. De instrument och maskiner som man tagit fram för mikroelektroniken har gjort det möjligt att studera naturens minsta beståndsdelar, till exempel Gecko-fötter, och gjort det möjligt att skapa material i nanometerstorlek. Molekyler och celler har visserligen alltid varit nanoteknik, men nu finns det möjligheter att koppla ihop biologi och elektronik.
Man frågar sig om nanopartiklar kan vara farliga. Det beror på om man talar om saker i nanostorlek eller om en yta som är nanostrukturerad. Om det kan avges stora mängder med små partiklar är det givetvis farligt, eftersom det kan skada lungorna om man inandas partiklarna. Men nanometerstora partiklar finns redan omkring oss, till exempel i avgaser och trafikdamm och tonerpulvret i en kopiator eller laserskrivare. En glasyta som är nanostrukturerad för att hålla sig ren avger dock inga partiklar.
Röntgendiffraktion
Materialfysiken söker ett samband mellan ett materials makroskopiska egenskaper och dess mikroskopiska, atomära och elektroniska struktur för att kunna förstå, modellera och modifiera sammansättning och egenskaper. Man frågar sig dels vilka slags atomer (kemisk identifiering) som förekommer i strukturen och dels hur de sitter geometriskt. I de flesta fasta material är atomerna arrangerade, åtminstone lokalt, i välordnade kristallstrukturer. För att bestämma kristallstrukturen används olika former av diffraktionsbaserade tekniker. Den vanligaste och mest kraftfulla formen är röntgendiffraktion (XRD). För att studera kristallstrukturer med atomavstånd på ett fåtal Ångström måste man använda våglängder i samma storleksordning. En vanlig röntgenkälla är \displaystyle \mathrm{Cu\, K_{\alpha}} med våglängden 1.54 Å. Röntgendiffraktion i kristaller kan betraktas som interferens mellan reflexer från närliggande plan i samma planskara, enligt figuren. Den infallande strålen beskrivs av vågvektorn \displaystyle \mathbf k, och den reflekterade strålen av vågvektorn \displaystyle \mathbf{k'}. Ändringen i vågvektor \displaystyle \Delta\,\mathbf{ k = k -\, k'}. För att interferensen ska vara konstruktiv gäller Braggs lag \displaystyle 2d\sin \theta = m\lambda som beskrivs i 5.3.
Elektronmikroskopi
Elektronmikroskopet är ett mångsidigt instrument som används för att erhålla strukturell, magnetisk och elektronisk information om ett prov. Med olika avbildningstekniker, elektrondiffraktion och spektroskopi kan dessa materialegenskaper bestämmas med en rumsupplösning ner till \displaystyle \mathrm{1Å}. Fokuserad elektron- eller jonstråle används för att analysera eller strukturera material på nanometernivå.
Elektronmikroskopi bidrar i sökandet efter unika material både inom tillämpad och grundläggande forskning genom analys på atomär nivå. Med denna kunskap kan ett materials meso- och makroskopiska egenskaper samt samband mellan struktur och mekaniska egenskaper karaktäriseras. Elektronmikroskopi lämpar sig väl för att studera strukturella förändringar och egenskaper hos polymerer, metaller, keramer och biologiska material. Nanokristallina material med kornstorlekar mellan en till tio nm uppvisar helt nya magnetiska, elektriska och optiska egenskaper. Högupplösande elektronmikroskopi är en kraftfull teknik för att studera kristallorientering, fas samt kemisk sammansätting hos ett elektrontransparent tunt prov. Elektronstrålens växelverkan med ett magnetiskt prov används för att studera och visualisera domänmönster samt magnetisering hos magnetiska endomänpartiklar. För detta används elektronholografi och magnetisk avbildning med Lorentzmikroskopi.
Spinntronik
Spinntronik använder elektronernas spinn för att hantera information. Spinnet är mätbart som magnetism och om man kan ställa in spinnet kan man använda elektronernas magnetiska nord- och sydpoler för att representera ettor och nollor. Det innebär att man kan göra de elektroniska kretsarna mycket mindre än vad som är tänkbart med vanlig elektronik.
Kvantbit
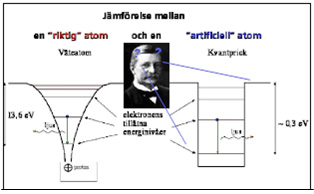
Kvantbit, eller qubit, från en. quantum binary digit, representerar den minsta enheten kvantinformation. Den fundamentala skillnaden mellan en kvantbit och klassisk bit är att den senare kan bara vara ha värdet \displaystyle 0 eller \displaystyle 1.En kvantbit motsvarar ett kvanttillstånd, en linjär superposition, s.k. kvantsuperposition.
Råd för inläsning
Tänk på att...
Begreppet laser (Light Amplification by Stimulated Emission of Radiation) har onekligen ett skimmer av science fiction över sig, men är idag en väldigt vanlig teknik som används i vårt dagliga liv. När vi handlar är det en laserstråle som läser av varornas priskoder, och det är laser som läser av informationen på våra cd- och dvd-skivor. På de flesta kontor finns det skrivare och kopiatorer som använder laser, och mycket av informationen som skickas mellan datorer och telefoner skickas via optiska fibrer, som även de fungerar med hjälp av laserljus.
Lästips
För dig behöver en längre förklaring eller som vill fördjupa dig ytterligare, vill vi tipsa om:
- HEUREKA! Fysik 2, kapitel 14, Atomen: sidorna 267 - 283
- Halliday and Resnick, Fundamentals of physics, Wiley