5.5 Kärnan
FörberedandeFysik
| Rad 62: | Rad 62: | ||
[[Bild:5.5_nukleoner.jpg]] | [[Bild:5.5_nukleoner.jpg]] | ||
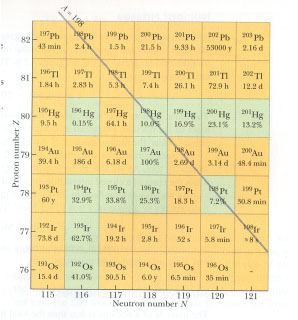
| - | Kemiskt identiska ämnen men med olika massor, sänder ut olika radioaktiv strålning. Dessa ämnen med samma kemiska egenskaper kallas ''isotoper''. De har olika ''atommassor'' (olika < | + | Kemiskt identiska ämnen men med olika massor, sänder ut olika radioaktiv strålning. Dessa ämnen med samma kemiska egenskaper kallas ''isotoper''. De har olika ''atommassor'' (olika <math>A</math>) men samma ''atomnummer'' (samma antal protoner <math>Z</math>). |
| - | Nuklider med samma < | + | Nuklider med samma <math>N</math>, men olika <math>Z</math>, kallas ''isotoner'' medan nuklider med samma <math>A</math> kallas ''isobarer''. Detta är icke att förväxla med värmelärans isobar som innebär samma tryck! |
Av de ca 2000 kända nukliderna är bara 280 stabila, resten är ''radioaktiva'', d.v.s. sönderfaller spontant. I naturen förekommer ett fåtal '''naturligt''' radioaktiva resten är framställda och kallas '''inducerat''' radioaktiva. | Av de ca 2000 kända nukliderna är bara 280 stabila, resten är ''radioaktiva'', d.v.s. sönderfaller spontant. I naturen förekommer ett fåtal '''naturligt''' radioaktiva resten är framställda och kallas '''inducerat''' radioaktiva. | ||
| - | Vid spridning av < | + | Vid spridning av <math>\alpha</math> -partiklar mot kärnor får man en avvikelse från Rutherfords teori för höga energier på a-partikeln (och lätta kärnor). Detta ger en möjlighet att bestämma kärnradien. Motsvarande försök har gjorts med elektroner (men det skedde senare eftersom det krävs hög energi för att ge elektronen en de Broglie-våglängd av en samma storlekordning som en kärnas diameter. Resultaten blev att kärnan kan (i en första approximation) betraktas som sfärisk med en radie <math>R</math>, som beror av masstalet <math>A</math> enligt |
| - | < | + | <math>R = R_0A^{1/3}</math> |
| - | där < | + | där <math>R_0 = 1{,}1\cdot10^{-15} \dots 1{,}4\cdot10^{-15}\, \textrm{m}</math> och det lägre värdet är från elektronspridning och den högre från <math>\alpha</math>-partikelspridning. |
| - | Kärnans massa, som kan mätas med hög precision anges i atomic mass units som definieras som massan av < | + | Kärnans massa, som kan mätas med hög precision anges i atomic mass units som definieras som massan av <math>1/12\,\,^{12}\mathrm{C}</math>-atom och har värdet |
| - | < | + | <math>1 \textrm{u} = 1,66056\cdot 10^{-27}\, \textrm{kg}</math> |
Det kan vara värt att lägga märke till att: | Det kan vara värt att lägga märke till att: | ||
| - | < | + | <math>\textrm{u}\,c^2 |
=\displaystyle\frac{m_\mathrm{u}\,c^2}{e} | =\displaystyle\frac{m_\mathrm{u}\,c^2}{e} | ||
=\displaystyle\frac{1{,}66056\cdot10^{-27}\:\mathrm{kg}\cdot(299792458\:\mathrm{ m/s})^2}{1{,}60217646\cdot10^{-19}\:\textrm{C}} | =\displaystyle\frac{1{,}66056\cdot10^{-27}\:\mathrm{kg}\cdot(299792458\:\mathrm{ m/s})^2}{1{,}60217646\cdot10^{-19}\:\textrm{C}} | ||
| - | = 931{,}494 \:\textrm{MeV}</ | + | = 931{,}494 \:\textrm{MeV}</math> |
och på samma sätt fås: | och på samma sätt fås: | ||
| - | < | + | <math>m_p\,c^2= 938{,}3 \textrm{ MeV}</math> |
| - | < | + | <math>m_n\,c^2= 939{,}6 \textrm{ MeV}</math> |
| - | < | + | <math>m_e\,c^2= 0{,}511 \textrm{ MeV}</math> |
| - | Kärnans massa, < | + | Kärnans massa, <math>M</math>, är mindre än summan än de ingående protonernas och neutronernas sammanlagda massor. Denna massdefekt <math>\Delta m</math> svarar mot en energi <math>E_{be} (>0)</math>, kärnans bindningsenergi. |
| - | < | + | <math>E_{be}= \Sigma(m\,c^2)\, –\, M\,c^2 = \Delta m\,c^2 </math> |
Om man tillför denna energi till kärnan kan man splittra den i dess beståndsdelar. | Om man tillför denna energi till kärnan kan man splittra den i dess beståndsdelar. | ||
| - | Om elektronernas bindningsenergier i atomen kan försummas kan < | + | Om elektronernas bindningsenergier i atomen kan försummas kan <math>E_{be}</math> för en kärna med <math>Z</math> protoner och elektroner, och <math>(A-Z)</math> neutroner skrivas |
| - | < | + | <math> E_{be} = Z m_p c^2 + (A-Z)m_n\,c^2 – (M - Z m_e)c^2</math> |
| - | där < | + | där <math>M</math> är atommassan (dvs kärna plus elektroner), <math>m_p</math> protonens massa, och <math>m_e</math> elektronens massa. Vi får alltså bindningsenergin som |
| - | < | + | <math>E_{be} = Zm_p\,c^2 + (A-Z)m_n\,c^2 + Z m_e c^2 – M\,c^2</math> |
Bindningsenergin/nukleon blir då | Bindningsenergin/nukleon blir då | ||
| - | < | + | <math>\epsilon = \displaystyle\frac{E_{be}}{A}</math> |
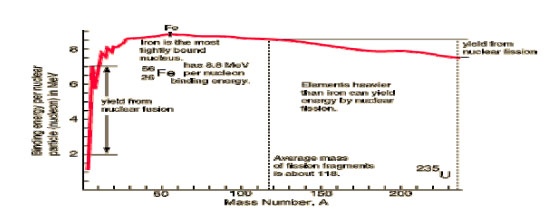
| - | där < | + | där <math>\varepsilon</math> beror av A enligt figuren nedan. |
[[Bild:5.5_epsilon.jpg]] | [[Bild:5.5_epsilon.jpg]] | ||
| + | |||
| + | =Fission= | ||
''Mer material kommer'' | ''Mer material kommer'' | ||
Versionen från 6 december 2017 kl. 10.39
| Teori | Övningar |
Mål och innehåll
Innehåll:
- Kärnans beståndsdelar
- Kärnans storlek (Vid spridning av \displaystyle \:\alpha\:-partiklar …)
- Kärnans bindningsenergi (Massa som kan mätas …)
- Fission och fusion
- Solens fusionsprocess
- Naturlig radioaktivitet
- \displaystyle \:\alpha\:-sönderfallet
- \displaystyle \:\beta\:-sönderfallet
- \displaystyle \:\gamma\:-sönderfallet
- Kol 14-metoden
Läromål
Efter detta avsnitt ska du ha lärt dig att:
- Redogöra för kärnans beståndsdelar.
- Beräkna kärnans storlek.
- Beräkna en given kärnas bindningsenergi.
- Redogöra för fissionsprocessen.
- Redogöra för fusionsprocessen.
- Förklara hur fusionen i vår sol fungerar.
- Förklara vad som menas med naturlig radioaktivitet.
- Redogöra för \displaystyle \:\alpha\:-sönderfallet.
- Redogöra för \displaystyle \:\beta\:-sönderfallet.
- Redogöra för \displaystyle \:\gamma\:-sönderfallet.
- Redogöra för \displaystyle \:^{14}C-metoden
FÖRFATTARE: Göran Tranströmer & Lars-Erik Berg, KTH Fysik
Kärnan
Thomson upptäcker elektronen 1897 (men dess massa var ännu okänd) och har en modell för hur atomen var sammansatt.
Rutherford (Geiger, Marsden) undersöker hans ”plumpudding-modell” och finner att atomens positiva laddning (och därmed dess massa) är koncentrerad till ett mycket litet område, en kärna, med en utsträckning som är 1/10000 av atomens. Eftersom man förväntade sig mycket små spridningsvinklar (”A bullet through a sack of snowballs”) så blev resultatet av experimentet oerhört förvånande. Med Rutherfords egna ord
"It was quite the most incredible event that ever happened to me in my life. It was almost as incredible as if you had fired a 15-inch shell at a piece of tissue paper and it came back and hit you".
Rutherford föreslår (1920) p+ och e- för att bilda neutral partikel i kärnan, som behövs eftersom massan av antalet protoner är mindre än totala massan/2.
Denna lösning duger ej (enligt Heisenbergs osäkerhetsrelationer) Neutronen postuleras därför (1928) och hittas 1932 av Chadwick.
Kärnan består av protoner och neutroner, (som med ett gemensamt namn kallas för nukleoner) och deras totala antal är masstalet \displaystyle A
- Antalet protoner i kärnan anges av atomnumret \displaystyle Z
- Antalet neutroner i kärnan anges av \displaystyle N
- \displaystyle A = Z + N
Kemiskt identiska ämnen men med olika massor, sänder ut olika radioaktiv strålning. Dessa ämnen med samma kemiska egenskaper kallas isotoper. De har olika atommassor (olika \displaystyle A) men samma atomnummer (samma antal protoner \displaystyle Z).
Nuklider med samma \displaystyle N, men olika \displaystyle Z, kallas isotoner medan nuklider med samma \displaystyle A kallas isobarer. Detta är icke att förväxla med värmelärans isobar som innebär samma tryck!
Av de ca 2000 kända nukliderna är bara 280 stabila, resten är radioaktiva, d.v.s. sönderfaller spontant. I naturen förekommer ett fåtal naturligt radioaktiva resten är framställda och kallas inducerat radioaktiva.
Vid spridning av \displaystyle \alpha -partiklar mot kärnor får man en avvikelse från Rutherfords teori för höga energier på a-partikeln (och lätta kärnor). Detta ger en möjlighet att bestämma kärnradien. Motsvarande försök har gjorts med elektroner (men det skedde senare eftersom det krävs hög energi för att ge elektronen en de Broglie-våglängd av en samma storlekordning som en kärnas diameter. Resultaten blev att kärnan kan (i en första approximation) betraktas som sfärisk med en radie \displaystyle R, som beror av masstalet \displaystyle A enligt
\displaystyle R = R_0A^{1/3}
där \displaystyle R_0 = 1{,}1\cdot10^{-15} \dots 1{,}4\cdot10^{-15}\, \textrm{m} och det lägre värdet är från elektronspridning och den högre från \displaystyle \alpha-partikelspridning.
Kärnans massa, som kan mätas med hög precision anges i atomic mass units som definieras som massan av \displaystyle 1/12\,\,^{12}\mathrm{C}-atom och har värdet
\displaystyle 1 \textrm{u} = 1,66056\cdot 10^{-27}\, \textrm{kg}
Det kan vara värt att lägga märke till att:
\displaystyle \textrm{u}\,c^2 =\displaystyle\frac{m_\mathrm{u}\,c^2}{e} =\displaystyle\frac{1{,}66056\cdot10^{-27}\:\mathrm{kg}\cdot(299792458\:\mathrm{ m/s})^2}{1{,}60217646\cdot10^{-19}\:\textrm{C}} = 931{,}494 \:\textrm{MeV}
och på samma sätt fås:
\displaystyle m_p\,c^2= 938{,}3 \textrm{ MeV}
\displaystyle m_n\,c^2= 939{,}6 \textrm{ MeV}
\displaystyle m_e\,c^2= 0{,}511 \textrm{ MeV}
Kärnans massa, \displaystyle M, är mindre än summan än de ingående protonernas och neutronernas sammanlagda massor. Denna massdefekt \displaystyle \Delta m svarar mot en energi \displaystyle E_{be} (>0), kärnans bindningsenergi.
\displaystyle E_{be}= \Sigma(m\,c^2)\, –\, M\,c^2 = \Delta m\,c^2
Om man tillför denna energi till kärnan kan man splittra den i dess beståndsdelar.
Om elektronernas bindningsenergier i atomen kan försummas kan \displaystyle E_{be} för en kärna med \displaystyle Z protoner och elektroner, och \displaystyle (A-Z) neutroner skrivas
\displaystyle E_{be} = Z m_p c^2 + (A-Z)m_n\,c^2 – (M - Z m_e)c^2
där \displaystyle M är atommassan (dvs kärna plus elektroner), \displaystyle m_p protonens massa, och \displaystyle m_e elektronens massa. Vi får alltså bindningsenergin som
\displaystyle E_{be} = Zm_p\,c^2 + (A-Z)m_n\,c^2 + Z m_e c^2 – M\,c^2
Bindningsenergin/nukleon blir då
\displaystyle \epsilon = \displaystyle\frac{E_{be}}{A}
där \displaystyle \varepsilon beror av A enligt figuren nedan.
Fission
Mer material kommer