2.5 Masscentrum och tyngdkraft
FörberedandeFysik
| (7 mellanliggande versioner visas inte.) | |||
| Rad 27: | Rad 27: | ||
:* Ställa upp och räkna ut masscentrum för partiklar och sammansatta kroppar. | :* Ställa upp och räkna ut masscentrum för partiklar och sammansatta kroppar. | ||
:* Beskriva vad som händer med masscentrum när man tar bort materia i en kropp (gör hål i kroppen).</div> | :* Beskriva vad som händer med masscentrum när man tar bort materia i en kropp (gör hål i kroppen).</div> | ||
| + | |||
| + | FÖRFATTARE: Göran Karlsson, KTH Mekanik | ||
| + | |||
=Masscentrum och tyngdpunkt= | =Masscentrum och tyngdpunkt= | ||
| Rad 35: | Rad 38: | ||
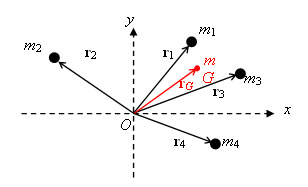
För fyra partiklar – som i figuren - definieras masscentrum så här: | För fyra partiklar – som i figuren - definieras masscentrum så här: | ||
| - | <math> | + | <math>\displaystyle \mathbf r\:_G = \frac{m_1\mathbf{r}_1\:+\: m_2\mathbf{r}_2\:+\:m_3\mathbf{r}_3\:+\:m_4\mathbf{r}_4}{m_1\:+\:m_2\:+\:m_3\:+\:m_4}</math> |
[[Bild:masscentrum.jpg|center]] | [[Bild:masscentrum.jpg|center]] | ||
| Rad 41: | Rad 44: | ||
Det är enkelt att inse hur man förfar med ett annat antal partiklar. | Det är enkelt att inse hur man förfar med ett annat antal partiklar. | ||
| - | Tyngdkraften | + | |
| + | =Tyngdkraften= | ||
I exemplet ovan är tyngdkraften | I exemplet ovan är tyngdkraften | ||
| - | + | <math> m\:\mathbf{g} = (m_1 + m_2 + m_3 + m_4)\:\mathbf{g} </math> | |
| - | och angriper i masscentrum G. | + | och angriper i masscentrum <math>G</math>. |
| - | Sammansatta kroppar | + | |
| + | =Sammansatta kroppar= | ||
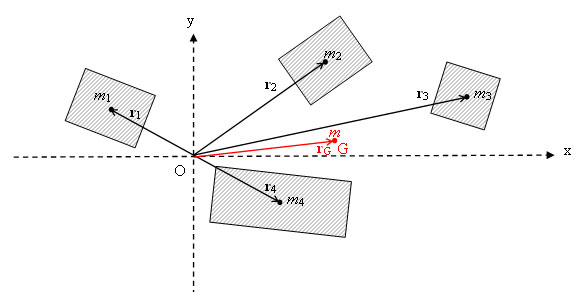
För sammansatta kroppar beräknas masscentrum som om varje delkropp var en partikel med delkroppens totala massa placerad i delkroppens masscentrum. T ex för fyra kroppar: | För sammansatta kroppar beräknas masscentrum som om varje delkropp var en partikel med delkroppens totala massa placerad i delkroppens masscentrum. T ex för fyra kroppar: | ||
| + | [[Bild:sammansattkropp.jpg|center]] | ||
| - | Hål | + | =Hål= |
Om man har kroppar med hål i så kan man behandla hålen som om de hade negativ massa. | Om man har kroppar med hål i så kan man behandla hålen som om de hade negativ massa. | ||
| - | |||
<div class="inforuta" style="width: 580px"> | <div class="inforuta" style="width: 580px"> | ||
| Rad 66: | Rad 71: | ||
====Lästips==== | ====Lästips==== | ||
| - | :Läs först i HEUREKA! Fysik kurs | + | :Läs först i ''HEUREKA! Fysik kurs 1'' kap 2:2–2:3 ''Hur beskriver man en kraft'' sid 24–26. |
====Länktips==== | ====Länktips==== | ||
| - | :Klicka här för mer information, bilder och en animation om 'Center of mass' i Wikipedia</div> | + | :[http://en.wikipedia.org/wiki/Center_of_mass Klicka här för mer information, bilder och en animation om 'Center of mass' i Wikipedia]</div> |
Nuvarande version
| Teori | Övningar |
Mål och innehåll
Innehåll
- Masscentrum och tyngdpunkt
- Tyngdkraften
- Sammansatta kroppar
- Masscentrum för kroppar med hål
Läromål
Efter detta avsnitt ska du ha lärt dig att:
- Matematiskt definiera begreppet masscentrum för partiklar och sammansatta kroppar med hjälp av vektorer.
- Redogöra för hur man bestämmer masscentrum grafiskt och praktiskt.
- Skilja mellan masscentrum och tyngdpunkt.
- Förklara varför man använder sig av masscentrum.
- Ställa upp och räkna ut masscentrum för partiklar och sammansatta kroppar.
- Beskriva vad som händer med masscentrum när man tar bort materia i en kropp (gör hål i kroppen).
FÖRFATTARE: Göran Karlsson, KTH Mekanik
Masscentrum och tyngdpunkt
Masscentrum och tyngdpunkt är viktiga begrepp i statik och stela kroppars dynamik. Man skiljer egentligen på begreppen masscentrum och tyngdpunkt. Men om en kropp befinner sig i ett homogent kraftfält så sammanfaller begreppen. Vi kommer att använda begreppen synonymt.
För fyra partiklar – som i figuren - definieras masscentrum så här:
\displaystyle \displaystyle \mathbf r\:_G = \frac{m_1\mathbf{r}_1\:+\: m_2\mathbf{r}_2\:+\:m_3\mathbf{r}_3\:+\:m_4\mathbf{r}_4}{m_1\:+\:m_2\:+\:m_3\:+\:m_4}
Det är enkelt att inse hur man förfar med ett annat antal partiklar.
Tyngdkraften
I exemplet ovan är tyngdkraften
\displaystyle m\:\mathbf{g} = (m_1 + m_2 + m_3 + m_4)\:\mathbf{g}
och angriper i masscentrum \displaystyle G.
Sammansatta kroppar
För sammansatta kroppar beräknas masscentrum som om varje delkropp var en partikel med delkroppens totala massa placerad i delkroppens masscentrum. T ex för fyra kroppar:
Hål
Om man har kroppar med hål i så kan man behandla hålen som om de hade negativ massa.