Lösning 3.2:2

FörberedandeFysik

(Skillnad mellan versioner)
Hoppa till: navigering, sök
Nuvarande version (15 mars 2018 kl. 10.57) (redigera) (ogör)
 
(2 mellanliggande versioner visas inte.)
Rad 1: Rad 1:
-
a) Periferi är <math>2\pi r=150\pi m</math> <math>v=farten=\frac{avstånd}{tid}=\frac{150\pi m}{30s}=15,7m/s</math><br\>
+
a) Periferi är <math>2\pi r=150\pi \mathrm{m}</math>
 +
 
 +
<math>v=\mathrm{farten}=\frac{\mathrm{avstånd}}{\mathrm{tid}}=\frac{150\pi \mathrm{m}}{30 \mathrm{s}}=15,7 \mathrm{m/s}</math><br\>
Rad 6: Rad 8:
[[Bild:losning_3_2_2_b.jpg]]
[[Bild:losning_3_2_2_b.jpg]]
-
Enligt figuren är v:s:<br\>
+
Enligt figuren är hastighetens<br\>
-
x-komponent<math>=-v\cos 60^\circ =-7,85m/s</math><br\>
+
x-komponent<math>=-v\cos 60^\circ =-7,85 \mathrm{m/s}</math><br\>
-
y-komponent<math>=-v\cos 30^\circ =-13,6m/s</math>
+
y-komponent<math>=-v\cos 30^\circ =-13,6\mathrm{m/s}</math>
Rad 14: Rad 16:
[[Bild:losning_3_2_2_c.jpg]]
[[Bild:losning_3_2_2_c.jpg]]
 +
 +
Storleken bestäms ur:<br\>
 +
 +
<math>\frac{v^2}{r}=\frac{(15,7\mathrm{m/s}^2)}{75\mathrm{m}}=3,3 \mathrm{m/s}^2</math><br\> Den är riktad inåt d v s i den negativa y-riktningen

Nuvarande version

a) Periferi är \displaystyle 2\pi r=150\pi \mathrm{m}

\displaystyle v=\mathrm{farten}=\frac{\mathrm{avstånd}}{\mathrm{tid}}=\frac{150\pi \mathrm{m}}{30 \mathrm{s}}=15,7 \mathrm{m/s}


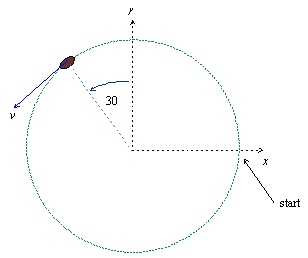
b) En 1/3 runt cirkeln betyder en vinkel på 120 grader runt cirkeln. Vi får följande figur.

Bild:losning_3_2_2_b.jpg

Enligt figuren är hastighetens
x-komponent\displaystyle =-v\cos 60^\circ =-7,85 \mathrm{m/s}
y-komponent\displaystyle =-v\cos 30^\circ =-13,6\mathrm{m/s}


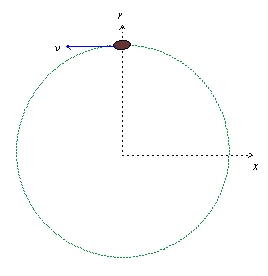
c) Bilen har en centripetalacceleration:

Bild:losning_3_2_2_c.jpg

Storleken bestäms ur:

\displaystyle \frac{v^2}{r}=\frac{(15,7\mathrm{m/s}^2)}{75\mathrm{m}}=3,3 \mathrm{m/s}^2
Den är riktad inåt d v s i den negativa y-riktningen

Den här artikeln är hämtad från http://wiki.math.se/wikis/forberedandefysik/index.php/L%C3%B6sning_3.2:2