FörberedandeFysik

Versionen från 23 december 2009 kl. 12.42 (redigera) Lena Chytraeus (Diskussion | bidrag) ← Gå till föregående ändring		Nuvarande version (15 mars 2018 kl. 12.57) (redigera) (ogör) Louwah (Diskussion | bidrag)
(8 mellanliggande versioner visas inte.)
Rad 3:		Rad 3:
	[[Bild:losning_3_2_3.jpg]]		[[Bild:losning_3_2_3.jpg]]
-	v_1\cos 16^\circ =25m/s \Rightarrow v_1=\frac{25m/s}{\cos 16^\circ}<br\>	+	<math>v_1\cos 16^\circ =25\mathrm{m/s} \Rightarrow v_1=\frac{25\mathrm{m/s}}{\cos 16^\circ}</math><br\>
	Vi söker:<br\>		Vi söker:<br\>
-	<math>v_1\sin 16,0^\circ =\frac{25m/s}{cos 16^\circ}=(25m/s)\tan 16,0^\circ =7,2m/s</math><br\>	+	<math>v_1\sin 16,0^\circ =\frac{25\mathrm{m/s}}{\cos 16^\circ}=(25\mathrm{m/s})\tan 16,0^\circ =7,2\mathrm{m/s}</math><br\>
-	b) Avstånd = fart gånger tid D=(25m/s)(1;5s)=37;5m
-	c) Den horisontella hastigheten är konstant under hela rörelsen. Vi måste bestämma den vertikala utgångshastigheten vystart.	+	b) <math>\mathrm{Avstånd} = \mathrm{fart} \cdot \mathrm{tid}</math>
-	Accelerationen är Àg vertikalt.	+
-	Vi behandlar den vertikala rörelsen som en separat rätlinjig rörelse.	+
-	Ekvationen: v=v0+at ger att 7;2m/s=v0startÀg(1;5)s=)vystart=21;9m/s	+
-	Enligt vektorteori är utgångsfarten lika med p(21;9m/s)2+(25m/s)2=33;2m/s	+	<math>D=(25\mathrm{m/s})(1,5\mathrm{s})=37,5\mathrm{m}</math><br\>
		+
		+
		+	c) Den horisontella hastigheten är konstant under hela rörelsen. Vi måste bestämma den vertikala utgångshastigheten <math>v_{ystart}</math>.<br\>
		+	Accelerationen är <math>-g</math> vertikalt.
		+	Vi behandlar den vertikala rörelsen som en separat rätlinjig rörelse.<br\>
		+	Ekvationen: <math>v=v_0+at</math> ger att <math>7,2\mathrm{m/s}=v_{0start} -g(1,5\mathrm{s}) \Rightarrow v_{ystart} =21,9\mathrm{m/s}</math><br\>
		+
		+	Enligt vektorteori är utgångsfarten lika med <math>\sqrt{(21,9\mathrm{m/s})^2+(25\mathrm{m/s})^2}=33,2\mathrm{m/s}</math>

---

Nuvarande version

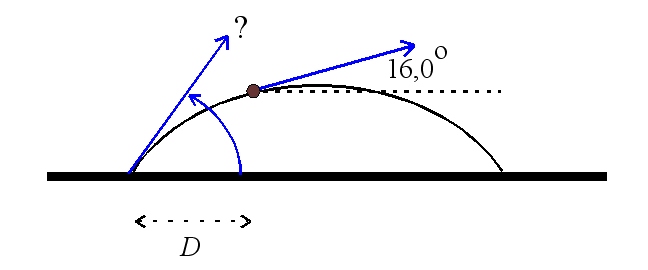
a) Låt bollens fart vara

\displaystyle v_1\cos 16^\circ =25\mathrm{m/s} \Rightarrow v_1=\frac{25\mathrm{m/s}}{\cos 16^\circ}
Vi söker:

\displaystyle v_1\sin 16,0^\circ =\frac{25\mathrm{m/s}}{\cos 16^\circ}=(25\mathrm{m/s})\tan 16,0^\circ =7,2\mathrm{m/s}

b) \displaystyle \mathrm{Avstånd} = \mathrm{fart} \cdot \mathrm{tid}

\displaystyle D=(25\mathrm{m/s})(1,5\mathrm{s})=37,5\mathrm{m}

c) Den horisontella hastigheten är konstant under hela rörelsen. Vi måste bestämma den vertikala utgångshastigheten \displaystyle v_{ystart}.
Accelerationen är \displaystyle -g vertikalt. Vi behandlar den vertikala rörelsen som en separat rätlinjig rörelse.
Ekvationen: \displaystyle v=v_0+at ger att \displaystyle 7,2\mathrm{m/s}=v_{0start} -g(1,5\mathrm{s}) \Rightarrow v_{ystart} =21,9\mathrm{m/s}

Enligt vektorteori är utgångsfarten lika med \displaystyle \sqrt{(21,9\mathrm{m/s})^2+(25\mathrm{m/s})^2}=33,2\mathrm{m/s}