Lösning 3.3:4
FörberedandeFysik
(Skillnad mellan versioner)
| (En mellanliggande version visas inte.) | |||
| Rad 8: | Rad 8: | ||
[[Bild:losning_3_3_4.2.jpg]] | [[Bild:losning_3_3_4.2.jpg]] | ||
| + | |||
| + | Kraftsumman på lådan nedför planet är:<br\> | ||
| + | |||
| + | <math>Mg\cdot\cos60^\circ - \frac{Mg}{10}</math><br\> | ||
| + | |||
| + | Om <math>a</math> är lådans acceleration, får vi enligt kraftekvationen<br\> | ||
| + | |||
| + | <math>Mg\cos60^\circ - \frac{Mg}{10} =Ma \Rightarrow g\cos60^\circ - \frac{g}{10}=a \Rightarrow a=3,93\,\mathrm{m/s}^2</math><br\> | ||
| + | |||
| + | <math>v=v_0+at \Rightarrow t=\frac{v-v_0}{a}=\frac{10\,\mathrm{m/s} - 5\,\mathrm{m/s}}{3,93\,\mathrm{m/s}^2}=1,3\,\mathrm{s}</math> | ||
Nuvarande version
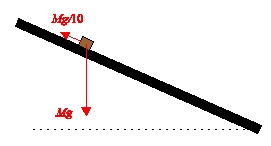
Låt massan vara \displaystyle M. Det betyder att tyngdkraften är \displaystyle M\cdot g och således är friktionskraften:
\displaystyle \frac{M\cdot g}{10}.
Vi är endast intresserade av krafterna längs planet.
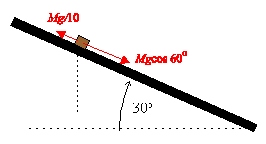
Kraftsumman på lådan nedför planet är:
\displaystyle Mg\cdot\cos60^\circ - \frac{Mg}{10}
Om \displaystyle a är lådans acceleration, får vi enligt kraftekvationen
\displaystyle Mg\cos60^\circ - \frac{Mg}{10} =Ma \Rightarrow g\cos60^\circ - \frac{g}{10}=a \Rightarrow a=3,93\,\mathrm{m/s}^2
\displaystyle v=v_0+at \Rightarrow t=\frac{v-v_0}{a}=\frac{10\,\mathrm{m/s} - 5\,\mathrm{m/s}}{3,93\,\mathrm{m/s}^2}=1,3\,\mathrm{s}