Lösning 3.4:1

FörberedandeFysik

(Skillnad mellan versioner)
Hoppa till: navigering, sök
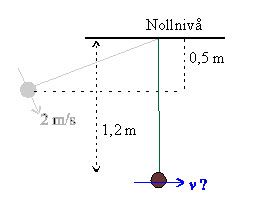
(Ny sida: a) Ju längre ner pendeln kommer desto högre är farten. Det betyder att hastigheten är maximal då pendeln är vertikal. Välj upphängningspunkten som nollnivå. [[Bild:losning_3_4_1....)
Nuvarande version (16 mars 2018 kl. 09.34) (redigera) (ogör)
 
(5 mellanliggande versioner visas inte.)
Rad 2: Rad 2:
[[Bild:losning_3_4_1.jpg]]
[[Bild:losning_3_4_1.jpg]]
 +
 +
Energiprincipen ger att summan av lägesenergi och kinetisk energi är konstant.<br\> Energin vid utgångsläget = Energin vid vertikalläget. Antag att partikeln har en massa <i>m</i>.
 +
 +
<math>\frac{1}{2}m(2\,\mathrm{m/s})^2-mg(0,5\,\mathrm{m})=\frac{1}{2}mv^2-mg(1,2\,\mathrm{m})</math>
 +
 +
 +
<math>\frac{1}{2}v^2=\frac{1}{2}(2\,\mathrm{m/s})^2+g(0,7\,\mathrm{m}) \Rightarrow v^2 = 4(\,\mathrm{m/s})^2+14(\,\mathrm{m/s})^2= </math>
 +
 +
<math>=18(\,\mathrm{m/s})^2 \Rightarrow v = \sqrt{18}\,\mathrm{m/s} = 4,24 \,\mathrm{m/s}</math>
 +
 +
 +
b) Anta att pendeln nätt och jämt klarar sig upp till sitt horisontella läge. Det betyder att den har noll hastighet då. Samtidigt har den noll lägesenergi. Vi kan dra slutsatsen att den minsta energi pendeln måste ha är noll.
 +
 +
Vi bestämmer pendelns energi <i>E</i> i utgångsläget.
 +
 +
<math>E=\frac{1}{2}m\cdot (2\,\mathrm{m/s})^2-mg(0,5\,\mathrm{m})</math>
 +
 +
<math>=\frac{1}{2}m\cdot 4(\,\mathrm{m/s})^2 - m(10\,\mathrm{m/s}^2)\cdot (0,5\,\mathrm{m})</math>
 +
 +
<math>=(2m-5m)(\,\mathrm{m/s})^2=-3m(\,\mathrm{m/s})^2<0</math>
 +
 +
Den når inte upp. Fundera även på om <math>m\cdot (\,\mathrm{m/s})^2</math> är en energienhet.

Nuvarande version

a) Ju längre ner pendeln kommer desto högre är farten. Det betyder att hastigheten är maximal då pendeln är vertikal. Välj upphängningspunkten som nollnivå.

Bild:losning_3_4_1.jpg

Energiprincipen ger att summan av lägesenergi och kinetisk energi är konstant.
Energin vid utgångsläget = Energin vid vertikalläget. Antag att partikeln har en massa m.

\displaystyle \frac{1}{2}m(2\,\mathrm{m/s})^2-mg(0,5\,\mathrm{m})=\frac{1}{2}mv^2-mg(1,2\,\mathrm{m})


\displaystyle \frac{1}{2}v^2=\frac{1}{2}(2\,\mathrm{m/s})^2+g(0,7\,\mathrm{m}) \Rightarrow v^2 = 4(\,\mathrm{m/s})^2+14(\,\mathrm{m/s})^2=

\displaystyle =18(\,\mathrm{m/s})^2 \Rightarrow v = \sqrt{18}\,\mathrm{m/s} = 4,24 \,\mathrm{m/s}


b) Anta att pendeln nätt och jämt klarar sig upp till sitt horisontella läge. Det betyder att den har noll hastighet då. Samtidigt har den noll lägesenergi. Vi kan dra slutsatsen att den minsta energi pendeln måste ha är noll.

Vi bestämmer pendelns energi E i utgångsläget.

\displaystyle E=\frac{1}{2}m\cdot (2\,\mathrm{m/s})^2-mg(0,5\,\mathrm{m})

\displaystyle =\frac{1}{2}m\cdot 4(\,\mathrm{m/s})^2 - m(10\,\mathrm{m/s}^2)\cdot (0,5\,\mathrm{m})

\displaystyle =(2m-5m)(\,\mathrm{m/s})^2=-3m(\,\mathrm{m/s})^2<0

Den når inte upp. Fundera även på om \displaystyle m\cdot (\,\mathrm{m/s})^2 är en energienhet.

Den här artikeln är hämtad från http://wiki.math.se/wikis/forberedandefysik/index.php/L%C3%B6sning_3.4:1