Lösning 3.4:3

FörberedandeFysik

(Skillnad mellan versioner)
Hoppa till: navigering, sök
Nuvarande version (16 mars 2018 kl. 09.54) (redigera) (ogör)
 
(En mellanliggande version visas inte.)
Rad 1: Rad 1:
-
a) Tyngdkraften är (48000 kg)g = 48000N
+
a) Tyngdkraften är <math>(48000 \,\mathrm{kg})g = 48000 \,\mathrm{N}</math>
[[Bild:losning_3_4_3.jpg]]
[[Bild:losning_3_4_3.jpg]]
-
Tyngdkraften har en komponent nedför vägen som är <math>48000\frac{1}{20}N = 2400N</math>
+
Tyngdkraften har en komponent nedför vägen som är <math>48000\frac{1}{20}\,\mathrm{N} = 2400 \,\mathrm{N}</math>
Eftersom lastbilen har en konstant hastighet måste krafterna längs vägen ta ut varandra.
Eftersom lastbilen har en konstant hastighet måste krafterna längs vägen ta ut varandra.
-
<math>F=2000N+2400N=4400N</math>
+
<math>F=2000\,\mathrm{N}+2400\,\mathrm{N}=4400\,\mathrm{N}</math>
-
<math>P = Pv \Rightarrow P=(4400N)(12m/s)=52800 W = 52,8 W</math>
+
<math>P = Pv \Rightarrow P=(4400\,\mathrm{N})(12\,\mathrm{m/s})=52800 \,\mathrm{W} = 52,8 \,\mathrm{kW}</math>
Vägen övergår till att bli horisontell. Motorn arbetar i samma takt,
Vägen övergår till att bli horisontell. Motorn arbetar i samma takt,
-
d v s med samma effekt och motståndskraften p g a friktion och luftmotstånd förblir densamma, <math>2000N</math>.
+
d v s med samma effekt och motståndskraften p g a friktion och luftmotstånd förblir densamma, <math>2000 \,\mathrm{N}</math>.
-
b) <i>F</i> är fortfarande <math>4400 N</math> omedelbart efter att vägen blivit horisontell. (Sedan ändras motorns kraft F eftersom hastigheten ändras). Newtons kraftekvation ger
+
b) <i>F</i> är fortfarande <math>4400 \,\mathrm{N}</math> omedelbart efter att vägen blivit horisontell. (Sedan ändras motorns kraft <i>F</i> eftersom hastigheten ändras). Newtons kraftekvation ger
-
<math>(4800kg)a=F-2000N=2400N \Rightarrow a = \frac{1}{2}m/s^2</math>
+
<math>(4800 \,\mathrm{kg})a=F-2000\,\mathrm{N}=2400\,\mathrm{N} \Rightarrow a = \frac{1}{2}\,\mathrm{m/s}^2</math>
Rad 24: Rad 24:
Motståndskraftens effekt = motorns effekt ger:
Motståndskraftens effekt = motorns effekt ger:
-
<math>(2000N)V_{max} = 52800W \Rightarrow V_{max} = \frac{52800}{2000}m/s=26,4 m/s</math>
+
<math>(2000 \,\mathrm{N})V_{max} = 52800\,\mathrm{W} \Rightarrow V_{max} = \frac{52800}{2000}\,\mathrm{m/s}=26,4 \,\mathrm{m/s}</math>

Nuvarande version

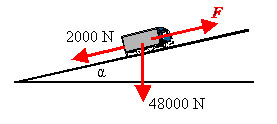
a) Tyngdkraften är \displaystyle (48000 \,\mathrm{kg})g = 48000 \,\mathrm{N}

Bild:losning_3_4_3.jpg

Tyngdkraften har en komponent nedför vägen som är \displaystyle 48000\frac{1}{20}\,\mathrm{N} = 2400 \,\mathrm{N}

Eftersom lastbilen har en konstant hastighet måste krafterna längs vägen ta ut varandra.

\displaystyle F=2000\,\mathrm{N}+2400\,\mathrm{N}=4400\,\mathrm{N}

\displaystyle P = Pv \Rightarrow P=(4400\,\mathrm{N})(12\,\mathrm{m/s})=52800 \,\mathrm{W} = 52,8 \,\mathrm{kW}

Vägen övergår till att bli horisontell. Motorn arbetar i samma takt, d v s med samma effekt och motståndskraften p g a friktion och luftmotstånd förblir densamma, \displaystyle 2000 \,\mathrm{N}.


b) F är fortfarande \displaystyle 4400 \,\mathrm{N} omedelbart efter att vägen blivit horisontell. (Sedan ändras motorns kraft F eftersom hastigheten ändras). Newtons kraftekvation ger

\displaystyle (4800 \,\mathrm{kg})a=F-2000\,\mathrm{N}=2400\,\mathrm{N} \Rightarrow a = \frac{1}{2}\,\mathrm{m/s}^2


c) Motorns kraft genererar en effekt som skall motverka motståndskraftens effekt då lastbilen har uppnått maximal hastighet \displaystyle V_{max}. (Innan den har uppnått den maximala hastigheten går en del av motorns effekt åt till att accelerera lastbilen).

Motståndskraftens effekt = motorns effekt ger:

\displaystyle (2000 \,\mathrm{N})V_{max} = 52800\,\mathrm{W} \Rightarrow V_{max} = \frac{52800}{2000}\,\mathrm{m/s}=26,4 \,\mathrm{m/s}

Den här artikeln är hämtad från http://wiki.math.se/wikis/forberedandefysik/index.php/L%C3%B6sning_3.4:3