Lösning 3.4:4

FörberedandeFysik

(Skillnad mellan versioner)
Hoppa till: navigering, sök
Nuvarande version (16 mars 2018 kl. 10.05) (redigera) (ogör)
 
(4 mellanliggande versioner visas inte.)
Rad 1: Rad 1:
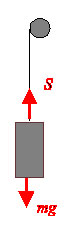
a) Eftersom lådan har en konstant hastighet, måste krafterna på lådan ta ut varandra.
a) Eftersom lådan har en konstant hastighet, måste krafterna på lådan ta ut varandra.
-
<math>S = mg = 1860N</math>
+
<math>S = mg = 1860\,\mathrm{N}</math> (<math>1870 \,\mathrm{N}</math> om <math>g</math> antas vara <math>9,82</math> snarare än <math>9,8 \,\mathrm{m/s}^2</math>)
[[Bild:losning_3_4_4.jpg]]
[[Bild:losning_3_4_4.jpg]]
-
b) Tiden <i>t</i> det tar för lådan att lyftas ett avståndpå <math>2,9 m</math> fås ur <math>tid=\frac{avstånd}{hastighet}</math>
+
b) Tiden <i>t</i> det tar för lådan att lyftas ett avstånd på <math>2,9 \,\mathrm{m}</math> fås ur <math>\,\mathrm{tid}=\frac{\,\mathrm{avstånd}}{\,\mathrm{hastighet}}</math>
 +
<math>t=\frac{2,9}{3,8}\,\mathrm{s}</math><br\>
 +
Eftersom <math>\,\mathrm{Arbete} = \,\mathrm{Effekt} \cdot \,\mathrm{tid}</math>, <math>\Rightarrow W=(7,3 \,\mathrm{kW})\displaystyle \left (\frac{2,9}{3,8}(\,\mathrm{s})\right) = 5,570 \,\mathrm{kJ}</math>.
-
<math>t=\frac{2,9}{3,8}s</math>
 
-
Eftersom Arbete = Effekt <math>\cdot</math> tid, <math>\Rightarrow W=(7,3 kW)\displaystyle \left \frac{2,9}{3,8}(s)\right = 5,570 kJ</math>.
 
 +
c) Lådan har nu en lägesenergiökning <math>mgH = 5,410 \,\mathrm{kJ}</math>
-
c) Lådan har nu en lägesenergiökning <math>mgH = 5,410 kJ</math>
+
Sammanfattning: Motorn har uträttat ett arbete på <math>5570 \,\mathrm{J}</math>, och systemet har fått en energiökning på <math>5410 \,\mathrm{J}</math>. Det betyder att <math>160 \,\mathrm{J}</math> har försvunnit som mekaniska energiförluster (omvandlats till värmeenergi o s v).
-
 
+
-
Sammanfattning: Motorn har uträttat ett arbete på <math>5570 J</math>, och systemet har fått en energiökning på <math>5410 J</math>. Det betyder att <math>160 J</math> har försvunnit som mekaniska energiförluster (omvandlats till värmeenergi o s v).
+

Nuvarande version

a) Eftersom lådan har en konstant hastighet, måste krafterna på lådan ta ut varandra.

\displaystyle S = mg = 1860\,\mathrm{N} (\displaystyle 1870 \,\mathrm{N} om \displaystyle g antas vara \displaystyle 9,82 snarare än \displaystyle 9,8 \,\mathrm{m/s}^2)

Bild:losning_3_4_4.jpg

b) Tiden t det tar för lådan att lyftas ett avstånd på \displaystyle 2,9 \,\mathrm{m} fås ur \displaystyle \,\mathrm{tid}=\frac{\,\mathrm{avstånd}}{\,\mathrm{hastighet}}

\displaystyle t=\frac{2,9}{3,8}\,\mathrm{s}
Eftersom \displaystyle \,\mathrm{Arbete} = \,\mathrm{Effekt} \cdot \,\mathrm{tid}, \displaystyle \Rightarrow W=(7,3 \,\mathrm{kW})\displaystyle \left (\frac{2,9}{3,8}(\,\mathrm{s})\right) = 5,570 \,\mathrm{kJ}.


c) Lådan har nu en lägesenergiökning \displaystyle mgH = 5,410 \,\mathrm{kJ}

Sammanfattning: Motorn har uträttat ett arbete på \displaystyle 5570 \,\mathrm{J}, och systemet har fått en energiökning på \displaystyle 5410 \,\mathrm{J}. Det betyder att \displaystyle 160 \,\mathrm{J} har försvunnit som mekaniska energiförluster (omvandlats till värmeenergi o s v).

Den här artikeln är hämtad från http://wiki.math.se/wikis/forberedandefysik/index.php/L%C3%B6sning_3.4:4