Lösning 4.5:6
FörberedandeFysik
(Skillnad mellan versioner)
| Rad 1: | Rad 1: | ||
| - | Spegelns bredd är <math>0,80 m</math>. Det finns ett antal olika sätt att lösa uppgiften på. En enklare metod är att räkna på likformiga trianglar. | + | Spegelns bredd är <math>0,80 \,\mathrm{m}</math>. Det finns ett antal olika sätt att lösa uppgiften på. En enklare metod är att räkna på likformiga trianglar. |
| - | + | ||
| - | <math>0,40/1,0 | + | Spegelns halva bredd förhåller sig till avståndet till ögat som halva väggbredden förhåller sig till avståndet till där den streckade linjen skär symmetriaxeln till väggen bakom ryggen. Halva spegelbredden är <math>0,40 \,\mathrm{m}</math>, avståndet mellan öga och spegel är <math>1,0 \,\mathrm{m}</math>. Avståndet till väggen från skärningspunkten är <math>4,0 \,\mathrm{m}</math><br\> |
| - | Från kant till kant på väggen bakom är det dubbelt så stort avstånd dvs <math>3,2 m</math> | + | <math>0,40/1,0=x/4,0 \Rightarrow x=1,6 \,\mathrm{m}</math> |
| + | |||
| + | Från kant till kant på väggen bakom är det dubbelt så stort avstånd dvs <math>3,2 \,\mathrm{m}</math> | ||
[[Bild:losning_4_5_6.jpg]] | [[Bild:losning_4_5_6.jpg]] | ||
Nuvarande version
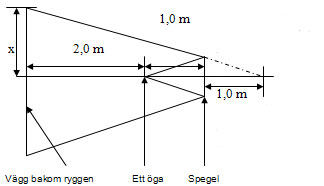
Spegelns bredd är \displaystyle 0,80 \,\mathrm{m}. Det finns ett antal olika sätt att lösa uppgiften på. En enklare metod är att räkna på likformiga trianglar.
Spegelns halva bredd förhåller sig till avståndet till ögat som halva väggbredden förhåller sig till avståndet till där den streckade linjen skär symmetriaxeln till väggen bakom ryggen. Halva spegelbredden är \displaystyle 0,40 \,\mathrm{m}, avståndet mellan öga och spegel är \displaystyle 1,0 \,\mathrm{m}. Avståndet till väggen från skärningspunkten är \displaystyle 4,0 \,\mathrm{m}
\displaystyle 0,40/1,0=x/4,0 \Rightarrow x=1,6 \,\mathrm{m}
Från kant till kant på väggen bakom är det dubbelt så stort avstånd dvs \displaystyle 3,2 \,\mathrm{m}